
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index
116 |
5 SYMMETRY GROUPS IN THREE DIMENSIONS |
FINITE ROTATION GROUPS IN THREE DIMENSIONS
We now proceed to show that the only finite proper rotation groups in three dimensions are the three symmetry groups of the regular solids, A4, S4, and A5 together with the cyclic and dihedral groups, Cn and Dn.
The unit sphere S2 = {x R3 ||x|| = 1} is mapped to itself by every element of O(3). Every rotation group fixing the origin is determined by its action on the unit sphere S2. By Theorem 5.10, every nonidentity element A SO(3) leaves precisely two antipodal points on S2 fixed. That is, there exists x S2 such that A(x) = x and A(−x) = −x. The points x and −x are called the poles of A. Let P be the set of poles of the nonidentity elements of a finite subgroup G of SO(3).
Proposition 5.14. G acts on the set, P , of poles of its nonidentity elements.
Proof. We show that G permutes the poles among themselves. Let A, B, be nonidentity elements of G, and let x be a pole of A. Then (BAB−1)B(x) = BA(x) = B(x), so that B(x) is a pole of BAB−1. Therefore, the image of any pole is another pole, and G acts on the set of poles.
We classify the rotation groups by considering the number of elements in the stabilizers and orbits of the poles. Recall that the stabilizer of a pole x, Stab x = {A G|A(x) = x}, is a subgroup of G, and that the orbit of x, Orb x = {B(x)|B G}, is a subset of the set P of poles. In Table 5.2 we look at the stabilizers and orbits of the poles of the rotation groups we have already discussed.
TABLE 5.2. Poles of the Finite Rotation Groups
Group G = |
Cn |
|
Dn |
|
|
A4 |
|
|
|
|
|G| = |
n |
|
2n |
|
|
12 |
|
|
Symmetries of |
n-agonal cone |
n-agonal cylinder |
|
tetrahedron |
|
|
|||
Looking down |
|
|
|
|
|
|
|
|
|
on the pole, x |
|
|
|
|
|
|
|
|
|
|Stab x| |
= |
n |
n |
2 |
2 |
n |
2 |
3 |
3 |
|Orb x| |
= |
1 |
1 |
n |
n |
2 |
6 |
4 |
4 |
Group G = |
S4 |
|
|
A5 |
|
|
|
|
|
|
|G| = |
24 |
|
|
60 |
|
|
|
|
Symmetries of |
cube |
or octahedron |
dodecahedron |
or icosahedron |
|
||||
Looking down |
|
|
|
|
|
|
|
|
|
on the pole, x |
|
|
|
|
|
|
|
|
|
|
|
or |
or |
or |
or |
|
or |
or |
|
|Stab x| |
= |
2 |
3 |
4 |
2 |
|
3 |
5 |
|
|Orb x| |
= |
12 |
8 |
6 |
30 |
|
20 |
12 |
|
FINITE ROTATION GROUPS IN THREE DIMENSIONS |
|
117 |
|||
|
x |
|
|
x |
x |
Rotation: |
|
|
|
|
|
p |
2p |
or |
4p |
p |
or p |
|
3 |
3 |
2 |
||
Looking down on |
x |
x |
|
|
x |
the pole x: |
|
|
|||
|
|
|
|
|
|
Order of the rotation: |
2 |
|
3 |
|
4 or 2 |
|
Figure 5.7. Rotations of the cube. |
|
|
||
We take Cn to be the rotation group of a regular n-agonal cone whose base is a regular n-gon. (The sloping edges of the cone must not be equal to the base edges if n = 3.) Dn is the rotation group of a regular n-agonal cylinder whose base is a regular n-gon. (The vertical edges must not be equal to the base edges if n = 4.)
Each stabilizer group, Stab x, is a cyclic subgroup of rotations of the solid about the axis through x. The orbit of x, Orb x, is the set of poles of the same type as x. As a check on the number of elements in the stabilizers and orbits, we have |G| = |Stab x||Orb x| for each pole x.
For example, the cube has three types of poles and four types of nontrivial elements in its rotation group; these are illustrated in Figure 5.7.
Theorem 5.15. Any finite subgroup of SO(3) is isomorphic to one of
Cn(n 1), Dn(n 2), A4, S4 or A5.
Proof. Let G be a finite subgroup of SO(3). Choose a set of poles x1, . . . , xr , one from each orbit. Let pi = |Stab xi | and qi = |Orb xi |, so that pi qi = n = |G|.
Each nonidentity element of G has two poles; thus the total number of poles, counting repetitions, is 2(n − 1). The pole xi occurs as a pole of a nonidentity element pi − 1 times. There are qi poles of the same type as xi . Therefore, the total number of poles, counting repetitions, is
r |
r |
2(n − 1) = qi (pi − 1) = (n − qi ),
|
|
i=1 |
|
|
|
|
i=1 |
|
|||
so |
|
2 |
|
|
r |
1 |
|
1 |
. |
|
|
2 |
|
|
|
|
( ) |
||||||
|
− |
|
|
|
= |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|||||
n |
pi |
|
i=1 |

118 5 SYMMETRY GROUPS IN THREE DIMENSIONS
If G is not the trivial group, n 2 and 1 2 − 2 < 2. Since xi is a pole of n
some nonidentity element, Stab xi contains a nonidentity element, and pi 2.
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|||
Therefore, |
|
|
− |
|
< 1. It follows from (*) that the number of orbits, r, must |
||||||||||
2 |
pi |
||||||||||||||
be 2 or 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If there are just two orbits, it follows that |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
2 − |
|
= 1 − |
|
+ 1 |
− |
|
|
|
|
|
|
|
|
|
|
n |
p1 |
p2 |
|||||
and 2 = |
n |
|
+ |
n |
= q1 + q2. Hence q1 = q2 = 1, and p1 = p2 = n. This means |
||||||||||
|
|
||||||||||||||
p1 |
p2 |
||||||||||||||
that x1 = x2, and there is just one axis of rotation. Therefore, G is isomorphic to the cyclic group Cn.
If there are three orbits, it follows |
that |
|
|
|
|||||||||||
2 |
|
1 |
1 |
1 |
|
||||||||||
2 − |
|
= |
1 − |
|
|
+ 1 − |
|
|
+ 1 − |
|
|
||||
n |
p1 |
p2 |
p3 |
||||||||||||
1 + |
2 |
= |
|
1 |
+ |
|
1 |
+ |
1 |
. |
(**) |
||||
|
|
|
|
|
|||||||||||
np1 p2 p3
Suppose that p1 p2 p3. If p1 3, we would have |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
+ |
|
+ |
|
|
= 1, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
p2 |
|
p3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
> 0. Hence p1 = 2 and q1 = |
n |
|
|
|
|
||||||||||||||||||||||||
which is a contradiction, since |
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
n |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
2 |
1 |
|
1 |
|
|
|
4, we would |
||||||||||||||||||||||||
Now 1 + |
|
|
= |
|
|
|
+ |
|
|
|
+ |
|
|
, so |
|
|
|
+ |
|
= |
|
|
+ |
|
. If p2 |
|
||||||||||||||||||||||||||
n |
2 |
p2 |
p3 |
|
2 |
n |
p2 |
p3 |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
have |
|
|
+ |
|
|
|
|
+ |
|
= |
|
|
, which is a contradiction, since |
|
|
> 0. Hence p2 |
||||||||||||||||||||||||||||||||||||
|
p2 |
p3 |
4 |
|
4 |
2 |
n |
|||||||||||||||||||||||||||||||||||||||||||||
is 2 or 3. The only possibilities are the following. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Case (i). p1 = |
2, p2 = 2, p3 = |
n |
, n is even and n 4, q1 = |
|
|
n |
, q2 |
= |
n |
, and |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
q3 = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Case (ii). p1 = 2, p2 = 3, p3 = 3, n = 12, q1 = 6, q2 = 4, and q3 = 4. Case (iii). p1 = 2, p2 = 3, p3 = 4, n = 24, q1 = 12, q2 = 8, and q3 = 6. Case (iv). p1 = 2, p2 = 3, p3 = 5, n = 60, q1 = 30, q2 = 20, and q3 = 12.
1 |
1 |
|
1 |
|
1 |
|
1 |
|
||
If p2 = 2 and p3 6, |
|
+ |
|
|
|
+ |
|
= |
|
, which contradicts (**), since |
p2 |
p3 |
3 |
6 |
2 |
||||||
2
> 0.
n
FINITE ROTATION GROUPS IN THREE DIMENSIONS |
119 |
Case (i). Let H = Stab x3. This is a group of rotations about one axis, and it is a cyclic group of order n/2. Any other element A that is not in H is of order 2 and is a half turn. Therefore, G = H H A, and G is isomorphic to Dn/2 of order n.
Case (ii). Let y1, y2, y3, and y4 be the four poles in Orb x2. Now p2 =
|Stab yi | = 3; thus Stab y1 permutes y2, y3, and y4 as in Figure 5.8. Therefore, ||y2 − y1|| = ||y3 − y1|| = ||y4 − y1||. We have similar results for Stab
y2 and Stab y3. Hence y1, y2, y3, and y4 are the vertices of a regular tetrahedron, and G is a subgroup of the symmetries of this tetrahedron. Since |G| = 12, G must be the whole rotation group, A4.
Case (iii). Let y1, y2, . . . , y6 be the six poles in Orb x3. Since p3 = 4, a rotation in Stab yi must fix two of the poles and rotate the other four cyclically. Hence y1, y2, . . . , y6 must lie at the vertices of a regular octahedron. Again, since |G| = 24, G must be the whole rotation group, S4, of this octahedron.
Case (iv). Let y1, y2, . . . , y12 be the 12 poles in Orb x3. Any element of order 5 in G must permute these poles and hence must fix two poles
and |
permute |
the |
others, |
as |
in |
Figure 5.9, in two disjoint 5-cycles, say |
|||||
|
3 4 5 |
6 |
|
2 |
|
3 |
4 |
5 |
10 |
6 |
|
2 |
|
Ž |
|
7 |
8 |
9 |
11 , where we denote the pole yi |
||||
by i. The points y , y , y , y , and y |
|
form a regular pentagon and their |
|||||||||
distances from y1 are all equal. Using similar results for rotations of order 5 about the other poles, we see that the poles are the vertices of an
icosahedron, |
and the group G is the proper rotation group, A5, of this |
icosahedron. |
|
Throughout this section we have considered only proper rotations. However, if we allow improper rotations as well, it can be shown that a finite subgroup
|
y2 |
|
|
|
y1 |
|
y3 |
|
|
|
|
|
Stab y1 |
y4 |
|
|
|
|
|
Figure 5.8 |
|
|
|
|
8 |
|
2 |
|
|
|
|
|
|
|
|
|
7 |
3 |
|
1 |
|
|
9 |
|
6 |
Stab y1 |
|
|
|
|
|||
12 |
11 |
4 |
|
|
|
|
|
|
|
|
|
10 |
5 |
|
Figure 5.9
120 |
5 SYMMETRY GROUPS IN THREE DIMENSIONS |
of O(3) is isomorphic to one of the groups in Theorem 5.15 or contains one of these groups as a normal subgroup of index 2. See Coxeter [27, Sec. 15.5] for a more complete description of these improper rotation groups.
CRYSTALLOGRAPHIC GROUPS
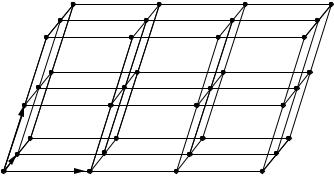
This classification of finite symmetries in R3 has important applications in crystallography. Many chemical substances form crystals and their structures take the forms of crystalline lattices. A crystal lattice is always finite, but in order to study its symmetries, we create a mathematical model by extending this crystal lattice to infinity. We define an ideal crystalline lattice to be an infinite set of points in R3 of the form
n1a1 + n2a2 + n3a3,
where a1, a2, and a3 form a basis of R3 and n1, n2, n3 Z. Common salt forms a cubic crystalline lattice in which a1, a2, and a3 are orthogonal vectors of the same length. Figure 5.10 illustrates a crystalline lattice.
This use of the term lattice is not the same as that in Chapter 2, where a lattice referred to a special kind of partially ordered set. To avoid confusion, we always use the term crystalline lattice here.
A subgroup of O(3) that leaves a crystalline lattice invariant is called a crystallographic point group. This is a finite subgroup of O(3) because there are only a finite number of crystalline lattice points that can be the images of a1, a2, and a3 when the origin is fixed.
However, not all finite subgroups of O(3) are crystallographic point groups. Suppose that A SO (3) leaves a crystalline lattice L invariant. Then, by Theorem 5.10, A is a rotation through an angle θ , and the trace of A is 1 + 2 cos θ . If we choose a basis for R3 consisting of the vectors a1, a2, a3 of the crystalline lattice L, the matrix representing A will have integer entries. The trace is invariant under change of basis, so the trace of A must be an integer. Hence 2 cos θ
|
a3 |
a2 |
a1 |
|
Figure 5.10. Crystalline lattice.
EXERCISES |
121 |
must be integral, and θ must be either kπ/2 or kπ/3, where k Z. It follows that every element of a crystallographic point group in SO(3) can only contain elements of order 1, 2, 3, 4, or 6.
It can be shown that every crystallographic point group in SO(3) is isomorphic to one of C1, C2, C3, C4, C6, D2, D3, D4, D6, A4, or S4.
If we allow reflections, the only other such groups in O(3) must contain one of these groups as a normal subgroup of index 2. Every one of these groups occurs in nature as the point group of at least one chemical crystal. See Coxeter [27, Sec. 15.6] or Lomont [31, Chap. 4, Sec. 4].
EXERCISES
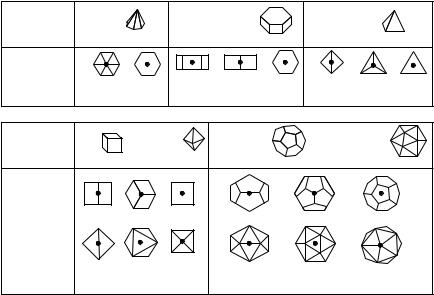
Find the group of proper rotations and the group of all rotations of the figures in Exercises 5.1 to 5.7.
5.1. |
|
|
5.2. |
|
|
5.3. |
|
|
5.4. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.5. 5.6. 5.7.
5.8.Let G be the subgroup of O(2) isomorphic to Dn. Find two matrices A and B so that any element of G can be written as a product of A’s and B’s.
5.9.What is the group of proper rotations of a rectangular box of length 3 cm, depth 2 cm, and height 2 cm?
Find the proper rotation group of the 13 Archimedean solids in Exercises 5.10 to 5.22. All the faces of these solids are regular polygons and all the vertices are similar. (See Cundy and Rollet [28] for methods on how to construct these solids.)
5.10. |
5.11. |
5.12. |
5.13. |
5.14. |
5.15. |
5.16. |
5.17. |
5.18. |
5.19. |
122 |
|
5 SYMMETRY GROUPS IN THREE DIMENSIONS |
5.20. |
5.21. |
5.22. |
5.23.It is possible to inscribe five cubes in a regular dodecahedron. One such cube is shown in Figure 5.11. Use these cubes to show that the rotation group of the dodecahedron is A5.
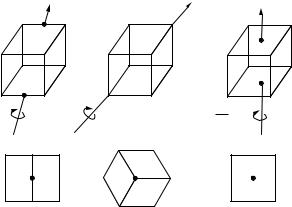
Figure 5.11. Cube inside a dodecahedron.
5.24.What is the proper symmetry group of a cube in which three faces, coming together at one vertex, are painted green and the other faces are red?
5.25.Find the group of all rotations (both proper and improper) of a regular tetrahedron.
5.26.Let G be the full symmetry group of the cube. Define f : G → S4 as in Theorem 5.12. Find the kernel of f and the order of G.
5.27.Let the vertices of a tetrahedron be (1, 1, 1), (−1, −1, 1), (−1, 1, −1), and (1, −1, −1). Find matrices in SO(3) of orders 2 and 3 that leave the tetrahedron invariant.
5.28.Let the vertices of a cube be (±1, ±1, ±1). Find matrices in SO(3) of orders 2, 3, and 4 that leave the cube invariant.
Find the symmetry groups of the chemical molecules in Exercises 5.29 to 5.31. (Assume that all of the C-C bonds are equivalent.)
5.29. |
H |
H |
5.30. |
CH3 |
CH3 |
5.31. |
H |
NO2 |
|
|
|
||||||
|
C |
C |
|
C |
C |
|
C |
C |
|
H C |
C H |
|
H C |
C H |
|
NO2 C |
C CH3 |
|
C |
C |
|
C |
C |
|
C |
C |
|
H |
H |
|
H |
H |
|
H |
NO2 |
|
Benzene |
|
Xylene |
|
Trinitrotoluene (TNT) |
|||

EXERCISES |
123 |
Find matrices in SO(3) that preserve the crystalline lattices described in Exercises 5.32 to 5.34, and find their crystallographic point groups. The points of the crystalline lattice are n1 a1 + n2 a2 + n3 a3 , where ni Z and the basis vectors ai are given below.
5.32. a1 |
= (1, 1, 0), a2 |
= (−1, 1, 0), a3 = (0, 1, 1). |
||
5.33. a1 |
= (1, 0, 0), a2 |
= (0, 1, 0), a3 |
= (0, 0, 2). |
√ |
|
|
√ |
|
|
5.34.a1 = (1, 0, 0), a2 = (0, −3 3, 3), a3 = (0, 3 3, 3).
5.35.Let G(n) denote the group of linear isometries of Rn.
(a) Show that E(n) = T (n)G(n) = G(n)T (n), where the product of subgroups is as defined in Exercise 4.43.
(b) Show that T (n) ∩ G(n) = {1Rn }.
(c) Use parts (a) and (b) to prove that E(n)/T (n) = G(n).

6
´
POLYA–BURNSIDE METHOD OF ENUMERATION
This chapter provides an introduction to the Polya´–Burnside method of counting the number of orbits of a set under the action of a symmetry group. If a group G acts on a set X and we know the number of elements of X, this method will enable us to count the number of different types of elements of X under the action of G.
For example, how many different chemical compounds can be obtained by attaching a CH3 or H radical to each carbon atom in the benzene ring of Figure 6.3? There are 26 different ways of attaching a CH3 or H radical on paper, but these do not all give rise to different compounds because many are equivalent under a symmetry. There are six different ways of attaching one CH3 radical and five H radicals, but they all give rise to the same compound. The dihedral group D6 acts on the 26 ways of attaching the radicals, and the number of different compounds is the number of orbits under the action of D6, that is, the number of formulas that cannot be obtained from each other by any rotation or reflection.
We have seen that the number of different switching circuits that can be obtained with n switches is 22n . This number grows very quickly as n becomes large. Table 2.11 gives the 16 switching functions of two variables; when n = 3, there are 256 different circuits, and when n = 4, there are 65,536 different circuits. However, many of these circuits are equivalent if we change the labels of the switches. That is, the symmetric group, Sn, acts on the 22n different circuits by permuting the labels of the switches. The number of nonequivalent circuits is the number of orbits under the action of Sn.
BURNSIDE’S THEOREM
Let G be a finite group that acts on a finite set X. The following theorem describes the number of orbits in terms of the number of elements left fixed
Modern Algebra with Applications, Second Edition, by William J. Gilbert and W. Keith Nicholson ISBN 0-471-41451-4 Copyright 2004 John Wiley & Sons, Inc.

BURNSIDE’S THEOREM |
125 |
by each element of G. It was first proved by W. Burnside in 1911 and was called Burnside’s lemma; it was not until 1937 that its applicability to many combinatorial problems was discovered by G. Polya´.
Theorem 6.1. Burnside’s Theorem. Let G be a finite group that acts on the elements of a finite set X. For each g G, let Fix g = {x X|g(x) = x}, the set of elements of X left fixed by g. If N is the number of orbits of X under
G, then
1
N = |G| g G | Fix g|.
Proof. We count the set S = {(x, g) X × G|g(x) = x} in two different ways. Consider Table 6.1, whose columns are indexed by the elements of X and whose rows are indexed by the elements of G. Put a value of 1 in the (x, g) position if g(x) = x; otherwise, let the entry be 0.
The sum of the entries in row g is the number |Fix g| of elements left fixed by g. The sum of the entries in column x is |Stab x|, the number of elements of G that fix x.
We can count the number of elements of S either by totaling the row sums or by totaling the column sums. Hence
|S| = |
|Fix g| = |
|Stab x|. |
g G |
|
x X |
Choose a set of representatives, x1, x2, . . . , xN , one from each orbit of X under G. If x is in the same orbit as xi , then Orb x = Orb xi , and by Theorem 4.40, |Stab x| = |Stab xi |. Hence
|
|
|
N |
|
|
· |
|
|
|
N |
|
|
|
|||
|
x |
|
|
|Stab x| = |
|
|
|
|||||||||
|
|
|
|Fix g| = |
= |
|
|
|
|
|
|
= |
|Orb xi ||Stab xi | = N · |G| |
||||
g |
G |
|
i |
1 |
Orb |
x |
i |
i |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
by Theorem 4.40. The theorem now follows. |
|
|
|
|||||||||||||
|
|
|
|
TABLE 6.1. Elements of S Correspond to the 1’s in |
||||||||||||
|
|
|
|
This Table |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Elements of X |
Row |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
Sums |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|Fix g| |
|
|
|
|
|
Elements |
|
g |
|
. . .1 0 1 |
|
|
1 1 0. . . |
|||||
|
|
|
|
of G |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
Column → |
|
|
|Stab x| |
|
|
||||
|
|
|
|
|
|
|
|
Sums |
|
|
|
|
|
|||
