
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index
242 |
|
|
|
|
|
12 LATIN SQUARES |
|
|
TABLE 12.12. Testing Three Different |
||||||
|
Drugs |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mon. |
Tues. |
Wed. |
Thurs. |
|
|
|
|
|
|
|
|
|
|
|
A |
aaa |
bbb |
ccc |
ddd |
|
|
Subject |
B |
bcd |
adc |
dab |
cba |
|
|
Group |
C |
cdb |
dca |
abd |
bac |
|
|
|
D |
dbc |
cad |
bda |
acb |
|
|
|
|
|
|
|
|
|
We recognize Euler’s problem of the 36 officers on parade mentioned at the beginning of the chapter as the problem of constructing two orthogonal latin squares of order 6. Euler not only conjectured that this problem was impossible to solve, but he also conjectured that it was impossible to find two orthogonal latin squares of order n, whenever n ≡ 2 mod 4.
Theorem 12.5 cannot be used to construct two such squares with order congruent to 2 modulo 4 because the only prime power of this form is 2, and then the theorem only gives one latin square. In 1899, G. Tarry, by exhaustive enumeration, proved that the problem of the 36 officers was insoluble. However, in 1959, Euler’s general conjecture was shown to be false, and in fact, Bose, Shrikhande, and Parker proved that there exist at least two orthogonal latin squares of order n, for any n > 6. Hence Proposition 12.4 is by no means the only way of constructing orthogonal latin squares. Laywine and Mullen [40] give a comprehensive survey of all the known results on latin squares up to the time of the book’s publication in 1998.
FINITE GEOMETRIES
The construction in Theorem 12.5 of n − 1 mutually orthogonal latin squares of order n, when n is a prime power, was first discovered by the American mathematician E. H. Moore in 1896, and was rediscovered by the Indian mathematical statistician R. C. Bose in 1938. (See Section 2.2 of Laywine and Mullin [40].) Bose also showed that there is a very close connection between orthogonal latin squares and geometries with a finite number of points and lines. These geometries are called affine planes.
An affine plane consists of a set, P , of points, together with a set, L, of subsets of P called lines. The points and lines must satisfy the following incidence axioms.
(i)Any two distinct points lie on exactly one line.
(ii)For each line l and point x not on l, there exists a unique line m containing x and not meeting l.
(iii)There exist three points not lying on a line.
We can define an equivalence relation of parallelism, / /, on the set of lines L, by defining l//m if l = m or l and m contain no common point. Axiom (ii) then states that through each point there is a unique line parallel to any other line. The
FINITE GEOMETRIES |
243 |
points and lines in the euclidean plane R2 form such a geometry with an infinite number of points.
If the geometry has only a finite number of points, it can be shown that there exists an integer n such that the geometry contains n2 points and n2 + n lines, and that each line contains n points, while each point lies on n + 1 lines. Such a finite geometry is called an affine plane of order n. In an affine plane of order n there are n + 1 parallelism classes (see Exercises 12.12 and 12.13).
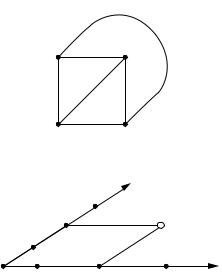
Figure 12.1 shows an affine plane of order 2 in which P = {a, b, c, d} and
L = {{a, b}, {c, d}, {a, c}, {b, c}, {b, d}, {a, d}}.
Bose showed that an affine plane of order n produces a complete set of n − 1 mutually orthogonal latin squares of order n, and conversely, that each set of n − 1 mutually orthogonal latin squares of order n defines an affine plane of order n.
Theorem 12.8. There exists an affine plane of order n if and only if there exist n − 1 mutually orthogonal latin squares of order n.
Proof. Suppose that there exists an affine plane of order n. We coordinatize the points as follows. Take any line and label the n points as 0, 1, 2, . . . , n − 1. This is called the x-axis, and the point labeled 0 is called the origin. Choose any other line through the origin and label the n points 0, 1, 2, . . . , n − 1 with 0 at the origin. This line is called the y-axis. A point of the plane is said to have coordinates (a, b) if the unique lines through the point parallel to the y and x-axes meet the axes in points labeled a and b, respectively. This is illustrated in Figure 12.2.
a |
b |
c d
Figure 12.1. Affine plane with four points.
y
n − 1
b |
(a, b) |
1
0 |
1 |
a |
x
n − 1
Figure 12.2. Coordinates in an affine plane.
244 12 LATIN SQUARES
There are n2 ordered pairs (a, b) corresponding to the n2 points of the plane. These points also correspond to the n2 cells of an n × n square where (a, b) refers to the cell in the ath row and bth column. We fill these cells with numbers in n − 1 different ways to produce n − 1 mutually orthogonal latin squares of order n.
Consider any complete set of parallel lines that are not parallel to either axis. Label the n parallel lines 0, 1, 2, . . . , n − 1 in any manner. Through each point, there is exactly one of these lines. In the cell (a, b) place the number of the unique line on which the point (a, b) is found. The numbers in these cells form a latin square of order n on {0, 1, . . . , n − 1}. No two numbers in the same row can be the same, because there is only one line through two points in the same row, namely, the line parallel to the x-axis. Hence each number appears exactly once in each row and, similarly, once in each column.
There are n − 1 sets of parallelism classes that are not parallel to the axes; each of these gives rise to a latin square. These n − 1 squares are mutually orthogonal because each line of one parallel system meets all n of the lines of any other system. Hence, when two squares are superimposed, each number of one square occurs once with each number of the second square.
Conversely, suppose that there exists a set of n − 1 mutually orthogonal latin squares of order n. We can relabel the elements, if necessary, so that these squares are based on S = {0, 1, 2, . . . , n − 1}. We define an affine plane with S2 as the set of points. A set of n points is said to lie on a line if there is a latin square with the same number in each of the n cells corresponding to these points, or if the n points all have one coordinate the same. It is straightforward to check that this is an affine plane of order n.
Corollary 12.9. There exists an affine plane of order n whenever n is the power of a prime.
Proof. This follows from Theorem 12.5.
The only known affine planes have prime power order. Because of the impossibility of solving Euler’s officer problem, there are no orthogonal latin squares of order 6, and hence there is no affine plane of order 6. In 1988, by means of a massive computer search, Lam, Thiel, and Swiercz showed that there was no affine plane of order 10. See Lam [39] for the story behind this two-decade search. By Theorem 12.8, there cannot exist nine mutually orthogonal latin squares of order 10. However, two mutually orthogonal latin squares of order 10 have been found, but not three such squares. Computers have also been used to search for many sets of mutually orthogonal latin squares of low order. See Chapter 2 of Laywine and Mullen [40] for further results on mutually orthogonal latin squares.
By the method of Theorem 12.8, we can construct an affine plane of order n from the Galois field GF(n) whenever n is a prime power. The set of points is
P = GF(n)2 = {(x, y)|x, y GF(n)}.

MAGIC SQUARES |
|
|
245 |
|
|
(0, a2) |
(1, a2) |
(a, a2) |
(a2, a2) |
|
(0, a) |
(1, a) |
(a, a) |
(a2, a) |
|
(0, 1) |
(1, 1) |
(a, 1) |
(a2, 1) |
|
(0, 0) |
(1, 0) |
(a, 0) |
(a2, 0) |
Figure 12.3. Affine plane of order 4 with the points of the line y = αx + α2 enlarged.
It follows from Proposition 12.4 that a line consists of points satisfying a linear equation in x and y with coefficients in GF(n). The slope of a line is defined in the usual way and is an element of GF(n) or is infinite. Two lines are parallel if and only if they have the same slope.
For example, if GF(4) = Z2(α) = {0, 1, α, α2}, the 16 points of the affine plane of order 4 are shown in Figure 12.3. The horizontal lines are of the form
y = constant
and have slope 0, whereas the vertical lines are of the form x = constant
and have infinite slope. The line
y = αx + α2
has slope α and contains the points (0, α2), (1, 1), (α, 0) and (α2, α). This line is parallel to the lines y = αx, y = αx + 1, and y = αx + α.
Given an affine plane of order n, it is possible to construct a projective plane of order n by adding a “line at infinity” containing n + 1 points corresponding to each parallelism class, so that parallel lines intersect on the line at infinity. The projective plane of order n has n2 + n + 1 points and n2 + n + 1 lines. Furthermore, any projective plane gives rise to an affine plane by taking one line to be the line at infinity. Hence the existence of a projective plane of order n is equivalent to the existence of an affine plane of the same order.
MAGIC SQUARES
Magic squares have been known for thousands of years, and in times when particular numbers were associated with mystical ideas, it was natural that a

246 |
12 LATIN SQUARES |
Publisher's Note:
Permission to reproduce this image online was not granted by the copyright holder. Readers are kindly requested to refer to the printed version of this article.
Figure 12.4. “Melancholia,” an engraving by Albrecht Durer¨. In the upper right there is a magic square of order 4 with the date of the engraving, 1514, in the middle of the bottom row. [Courtesy of Staatliche Museen Kupferstichkabinett, photo by Walter Steinkopf.]
square that displays such symmetry should have been deemed to have magical properties. Figure 12.4 illustrates an engraving by Durer,¨ made in 1514, that contains a magic square. Magic squares have no applications, and this section is included for amusement only.
MAGIC SQUARES |
247 |
A magic square of order n consists of the integers 1 to n2 arranged in an n × n square array so that the row sums, column sums, and corner diagonal sums are all the same.
The sum of each row must be n(n2 + 1)/2, which is 1/n times the sum of all the integers from 1 to n2. For example, in Durer’s¨ magic square of Figure 12.4, the sum of each row, column, and diagonal is 34.
It is an interesting exercise to try to construct such squares. We show how to construct some magic squares from certain pairs of orthogonal latin squares. See Ball et al. [38] and Laywine and Mullen [40] for other methods of constructing magic squares.
Let K = (kij ) and L = (lij ) be two orthogonal latin squares of order n on the set S = {0, 1, . . . , n − 1}. Superimpose these two squares to form a square M = (mij ) in which the elements of M are numbers in the base n, whose first digit is taken from K and whose second digit is taken from L. That is, mij = n · kij + lij . Since K and L are orthogonal, all possible combinations of two elements from S occur exactly once in M. In other words, all the numbers from 0 to n2 − 1 occur in M.
Now add 1 to every element of M to obtain the square M = mij , where
mij = mij + 1.
Lemma 12.10. The square M contains all the numbers between 1 and n2 and is row and column magic; that is, the sums of each row and of each column are the same.
Proof. In any row or column of M, each number from 0 to n − 1 occurs exactly once as the first digit and exactly once as the second digit. Hence the sum is
(0 + 1 + · · · + n − 1)n + (0 + 1 + · · · + n − 1)
= (n + 1)(n − 1)n/2 = n(n2 − 1)/2.
Therefore, each row or column sum of M is n(n2 − 1)/2 + n = n(n2 + 1)/2.
Example 12.11. Construct the square M from the two orthogonal latin squares, K and L, in Table 12.13.
Solution. Table 12.13 illustrates the superimposed square M in base 3 and in
base 10. By adding one to each element, we obtain the magic square M . |
|
|
Theorem 12.12. If K and L are orthogonal latin squares of order |
n on |
the |
set {0, 1, 2, . . . , n − 1} and the sum of each of the diagonals of K |
and L is |
|
n(n − 1)/2, then the square M derived from K and L is a magic square of order n.
248 |
|
|
|
|
|
|
|
|
|
|
12 LATIN SQUARES |
|
|
TABLE 12.13. Construction of a Magic |
|
|
|||||||||
|
Square of Order 3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
0 |
|
0 |
2 |
1 |
|
10 |
22 |
01 |
|
|
0 |
1 |
2 |
|
2 |
1 |
0 |
|
02 |
11 |
20 |
|
|
2 |
0 |
1 |
|
1 |
0 |
2 |
|
21 |
00 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
L |
M (in base 3) |
||||
|
|
|
|
|
|
|
|
|
|
3 |
8 |
1 |
|
4 |
9 |
2 |
|
|
2 |
4 |
6 |
|
3 |
5 |
7 |
|
|
7 |
0 |
5 |
|
8 |
1 |
6 |
|
|
|
|
|
|
|
|
||
M (in base 10) |
|
|
M |
|
|
|||
Proof. Lemma 12.10 shows that the sum of each row and each column is
2 |
+ 1)/2. |
A similar argument shows that the sum of each diagonal is also |
n(n2 |
||
n(n |
+ 1)/2. |
|
There are two common ways in which the sum of the diagonal elements of
Kand L can equal n(n − 1)/2.
(i)The diagonal is a permutation of {0, 1, . . . , n − 1}.
(ii)If n is odd, every diagonal element is (n − 1)/2.
Both these situations occur in the squares K and L of Table 12.13; thus the square M , which is constructed from these, is a magic square.
Example 12.13. Construct a magic square of order 4 from two orthogonal latin squares in Table 12.9.
Solution. By replacing 0, 1, α, α2 by 0, 1, 2, 3, in any order, the squares L2 and L3 in Table 12.9 satisfy the conditions of Theorem 12.12, because the
TABLE 12.14. Construction of a Magic
Square of Order 4
0 |
1 |
2 |
3 |
|
3 |
2 |
0 |
1 |
2 |
3 |
0 |
1 |
|
1 |
0 |
2 |
3 |
3 |
2 |
1 |
0 |
|
2 |
3 |
1 |
0 |
1 |
0 |
3 |
2 |
|
0 |
1 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
L3 |
|
03 |
12 |
20 |
31 |
|
4 |
7 |
9 |
14 |
21 |
30 |
02 |
13 |
|
10 |
13 |
3 |
8 |
32 |
23 |
11 |
00 |
|
15 |
12 |
6 |
1 |
10 |
01 |
33 |
22 |
|
5 |
2 |
16 |
11 |
|
|
|
|
|
|
|
|
|
M (in base 4) |
M |
