DIVISORS

It follows that d is the unique integer in P that is a divisor of both a and b, and is a multiple of every such common divisor (hence the name). Similarly, m is the unique integer in P that is a multiple of both a and b, and is a divisor of every such common multiple. For example, gcd(2, 3) = 1 and gcd(12, 28) = 4, while lcm(2, 3) = 6 and lcm(12, 28) = 84.

With this background, we can describe some new examples of boolean algebras. Given n P, let

Dn = {d P|d divides n}.

It is clear that gcd and lcm are commutative binary operations on Dn, and it is easy to verify that the zero is 1 and the unit is n. To prove the distributive laws, let a, b, and c be elements of Dn, and write

a = p1a1 p2a2 · · · prar , b = p1b1 p2b2 · · · prbr , and c = p1c1 p2c2 · · · prcr ,

where p1, p2, . . . , pr are the distinct primes dividing at least one of a, b, and c, and where ai 0, bi 0, and ci 0 for each i. Then the first distributive law states that

gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c)).

If we write out the prime factorization of each side in terms of the primes pi , this holds if and only if for each i, the powers of pi are equal on both sides, that is,

min(ai , max(bi , ci )) = max(min(ai , bi ), min(ai , ci )).

To verify this, observe first that we may assume that bi ci (bi and ci can be interchanged without changing either side), and then check the three cases ai bi , bi ai ci , and ci ai separately. Hence the first distributive law holds; the other distributive law and the associative laws are verified similarly. Thus (Dn, gcd, lcm) satisfies all the axioms for a boolean algebra except for the existence of a complement.

But complements need not exist in general: For example, 6 has no complement in D18 = {1, 2, 3, 6, 9, 18}. Indeed, if 6 has a complement 6 in D18, then gcd(6, 6 ) = 1, so we must have 6 = 1. But then lcm(6, 6 ) = 6 and this is not the unit of D18. Hence 6 has no complement, so D18 is not a boolean algebra. However, all is not lost. The problem in D18 is that the prime factorization 18 = 2 · 32 has a repeated prime factor. An integer n P is called square-free if it is a product of distinct primes with none repeated (for example, every prime is square-free, as are 6 = 2 · 3, 10 = 2 · 5, 30 = 2 · 3 · 5, etc.) If n is square-free, it is routine to verify that the complement of d Dn is d = n/d, and we have

Example 2.15. If n P is square-free, then (Dn, gcd, lcm, ) is a boolean algebra where d = n/d for each d Dn.

The interpretations of the various boolean algebra terms are given in Table 2.8.

A relation satisfying the three properties in Proposition 2.17 is called a partial order relation, and a set with a partial order on it is called a partially ordered set or poset for short. The interpretation of the partial order in various boolean algebras is given in Table 2.9.

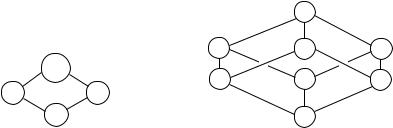
A partial order on a finite set K can be displayed conveniently in a poset diagram in which the elements of K are represented by small circles. Lines are drawn connecting these elements so that there is a path from A to B that is always directed upward if and only if A B. Figure 2.15 illustrates the poset diagram of the boolean algebra of subsets (P ({a, b}, )∩, , −). Figure 2.16 illustrates the boolean algebra D110 = {1, 2, 5, 11, 10, 22, 55, 110} of positive divisors of 110 = 2 · 5 · 11. The partial order relation is divisibility, so that there is an upward path from a to b if and only if a divides b.

The following proposition shows that has properties similar to those of the inclusion relation in sets.

Proposition 2.18. If A, B, C are elements of a boolean algebra (K, , , ), then the following relations hold:

(i)A B A.

(ii)A A B.

(iii)A C and B C implies that A B C.

(iv)A B if and only if A B = 0.

(v)0 A and A 1 for all A.

Proof

(i)(A B) A = (A A) B = A B so A B A.

(ii)A (A B) = A, so A A B.

(iii)(A B) C = (A C) (B C) = A B.

(iv)If A B, then A B = A and A B = A B B = A 0 = 0. On

the other hand, if A B = 0, then A B because

A = A 1 = A (B B ) = (A B) (A B )

= (A B) 0 = A B.

(v) 0 A = 0 and A 1 = A.

Not all posets are derived from boolean algebras. A boolean algebra is an extremely special kind of poset. We now determine conditions which ensure that a poset is indeed a boolean algebra. Given a partial order on a set K, we have to find two binary operations that correspond to the meet and join.

An element d is said to be the greatest lower bound of the elements a and b in a partially ordered set if d a, d b, and x is another element, for which x a, x b, then x d. We denote the greatest lower bound of a and b by a b. Similarly, we can define the least upper bound and denote it by . It follows from the antisymmetry of the partial order relation that each pair of elements a and b can have at most one greatest lower bound and at most one least upper bound.

A lattice is a partially ordered set in which every two elements have a greatest lower bound and a least upper bound. Thus Dn is a lattice for every integer n P, so by the discussion preceding Example 2.15, D18 is a lattice that is not a boolean algebra (see Figure 2.17).

We can now give an alternative definition of a boolean algebra in terms of a lattice: A boolean algebra is a lattice that has universal bounds (that is, elements 0 and 1 such that 0 a and a 1 for all elements a) and is distributive and complemented (that is, the distributive laws for and hold, and complements exist). It can be verified that this definition is equivalent to our original one.

In Figure 2.18, the elements c and d have a least upper bound b but no greatest lower bound.

We note in passing that the discussion preceding Example 2.15 shows that for each n P, the poset Dn is a lattice in which the distributive laws hold, but it is not a boolean algebra unless n is square-free. For further reading on lattices in applied algebra, consult, Davey and Priestley [16] or Lidl and Pilz [10].