
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index
96 |
|
|
|
|
|
4 |
QUOTIENT GROUPS |
|
TABLE 4.6. Groups of Low Order |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Order |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Abelian groups |
{e} |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
|
|
|
|
C2 × C2 |
|
|
|
C4 × C2 |
Non-abelian groups |
|
|
|
|
|
|
|
C2 × C2 × C2 |
|
|
|
|
|
S3 |
|
D4 |
|
|
|
|
|
|
|
|
|
Q |
ACTION OF A GROUP ON A SET
The concept of a group acting on a set X is a slight generalization of the group of symmetries of X. It is equivalent to considering a subgroup of S(X). This concept is useful for determining the order of the symmetry groups of solids in three dimensions, and it is indispensable in Chapter 6, when we look at the Polya´–Burnside method of enumerating sets with symmetries.
The group (G, ·) acts on the set X if there is a function
ψ: G × X → X
such that when we write g(x) for ψ(g, x), we have:
(i)(g1g2)(x) = g1(g2(x)) for all g1, g2 G, x X.
(ii)e(x) = x if e is the identity of G and x X.
Proposition 4.37. If g is an element of a group G acting on the set X, then
the function g: X → X, |
which |
|
maps |
x to |
g(x), |
is a bijection. This defines |
|||||||||
a morphism |
|
|
χ: G → S(X) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
from G to the group of symmetries of X. |
|
|
|
|
|
|
|
||||||||
Proof. The function |
g: X → X |
is |
injective because if g(x) = g(y), |
then |
|||||||||||
g−1g(x) |
= |
g−1g(y), and |
e(x) |
= |
e(y) or x |
= |
y. It is surjective because if z |
|
X, |
||||||
|
|
|
|
||||||||||||
|
|
g(g−1(z)) |
= |
gg |
−1(z) |
= |
e(z) |
= |
z. |
|
|
||||
|
|
|
|
|
|
|
|||||||||
Hence g is bijective, and g can be considered as an element of S(X), the group of symmetries of X.
The function χ: G → S(X), which takes the element g G to the bijection g: X → X, is a group morphism because χ(g1g2) is the function from X to X defined by χ(g1g2)(x) = (g1g2)(x) = (g1(g2(x)) = χ(g1) Ž χ(g2)(x); thus χ(g1g2) = χ(g1) Ž χ(g2).
If Kerχ = {e}, then χ is injective, and the group G is said to act faithfully on the set X. G acts faithfully on X if the only element of G, which fixes every

ACTION OF A GROUP ON A SET |
|
|
|
97 |
|||
|
|
g |
|
1 |
|
||
|
|
|
2 |
|
|
||
2 |
1 |
|
3 |
4 |
|||
6 |
|
|
5 |
|
|||
|
h |
|
|
|
|||
|
|
|
|
|
|
|
|
3 |
6 |
|
|
|
|
|
|
4 |
5 |
7 |
|
8 |
|
||
|
|
|
|
|
|
||
Figure 4.4. C2 |
acting on a hexagon. |
Figure 4.5. C3 |
acting on a cube. |
||||
element of X, is the identity e G. In this case, we identify G with Imχ and regard G as a subgroup of S(X).
For example, consider the cyclic group of order 2, C2 = {e, h}, acting on the regular hexagon in Figure 4.4, where h reflects the hexagon about the line joining vertex 3 to vertex 6. Then C2 acts faithfully and can be identified with the subgroup {(1), (15) Ž (24)} of D6.
The cyclic group C3 = {e, g, g2} acts faithfully on the cube in Figure 4.5, where g rotates the cube through one-third of a revolution about a line joining two opposite vertices. This group action can be considered as the subgroup {(1), (163) Ž (457), (136) Ž (475)} of the symmetry group of the cube.
Proposition 4.38. If G acts on a set X and x X, then
Stab x = {g G|g(x) = x}
is a subgroup of G, called the stabilizer of x. It is the set of elements of G that fix x.
Proof. Stab x is a subgroup because
(i)If g1, g2 Stab x, then (g1g2)(x) = g1(g2(x)) = g1(x) = x, so g1g2
Stab x.
(ii) If g Stab x, then g−1(x) = x, so g−1 Stab x. |
|
The set of all images of an element x X under the action of a group G is called the orbit of x under G and is denoted by
Orb x = {g(x)|g G}.
The orbit of x is the equivalence class of x under the equivalence relation on X in which x is equivalent to y if and only if y = g(x) for some g G. If π is a permutation in Sn, the subgroup generated by π acts on the set {1, 2, . . . , n}, and this definition of orbit agrees with our previous one.
A graphic illustration of orbits can |
be obtained |
by looking at the group |
||||
of matrices |
|
sin θ |
− cos θ θ |
|
R |
|
SO(2) |
|
|
||||
|
= |
cos θ |
sin θ |
|
|
|
|
|
|
|
|
|
|
98 |
4 QUOTIENT GROUPS |
under matrix multiplication. This group is called the special orthogonal group and is isomorphic to the circle group W . SO(2) acts on R2 as follows. The matrix M SO(2) takes the vector x R2 to the vector Mx. The orbit of any element x R2 is the circle through x with center at the origin. Since the origin is the only fixed point for any of the nonidentity transformations, the stabilizer of the origin is the whole group, whereas the stabilizer of any other element is the subgroup consisting of the identity matrix only.
The orbits of the cyclic group C2 acting on the hexagon in Figure 4.4 are {1, 5}, {2, 4}, {3}, and {6}.
There is an important connection between the number of elements in the orbit of a point x and the stabilizer of that point.
Lemma 4.39. If G acts on X, then for each x X
|G: Stab x| = |Orb x|.
Proof. Let H = Stab x and define the function
ξ : G/H → Orb x
by ξ(Hg) = g−1(x). This is well defined on cosets because if Hg = H k, then
k = hg for some h H , so k−1(x) = (hg)−1(x) = g−1h−1(x) = g−1(x), since h−1 H = Stab x.
The function ξ is surjective by the definition of the orbit of x. It is also injective, because ξ(Hg1) = ξ(Hg2) implies that g1−1(x) = g2−1(x), so g2g1−1(x) = x
and g2g1−1 Stab x = H . Therefore, ξ is a bijection, and the result follows.
Note that ξ is not a morphism. G/Stab x is just a set of cosets because Stab x is not necessarily normal. Furthermore, we have placed no group structure on Orb x.
Theorem 4.40. If the finite group G acts on a set X, then for each x X, |
|
|G| = |Stab x||Orb x|. |
|
Proof. This follows from Lemma 4.39 and Corollary 4.8. |
|
Example 4.41. Find the number of proper rotations of a cube. |
|
Solution. Let G be the group of proper rotations of a cube; that is, rotations that can be carried out in three dimensions. The stabilizer of the vertex 1 in Figure 4.6 is Stab 1 = {(1), (245) Ž (386), (254) Ž (368)}. The orbit of 1 is the set of all the vertices, because there is an element of G that will take 1 to any other vertex. Therefore, by Theorem 4.40,
|G| = |Stab 1| |Orb 1| = 3 · 8 = 24. |
|
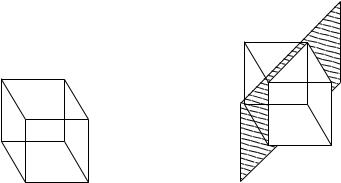
ACTION OF A GROUP ON A SET |
99 |
2 1
3 4
6 5
7 8
Figure 4.6. Cube. |
Figure 4.7. Reflection in a plane. |
The full symmetry group of the cube would include improper rotations such as the reflection in the plane as shown in Figure 4.7. This induces the permutation (24) Ž (68) on the vertices, and it cannot be obtained by physically rotating the cube in three dimensions. Under this group
Stab 1 = {(1), (245) Ž (368), (254) Ž (386), (24) Ž (68), (25) Ž (38), (45) Ž (36)},
so the order of the full symmetry group of the cube is
|Stab 1||Orb 1| = 6.8 = 48.
Therefore, there are 24 proper and 24 improper rotations of the cube.
The article by Shapiro [32] contains many applications, mainly to group theory, of the actions of a group on a set.
We conclude by mentioning the action of the symmetric group Sn on the set of polynomials in n variables x1, x2, . . . , xn. A permutation σ Sn acts on a polynomial f = f (x1, x2, . . . , xn) by permuting the variables:
σ (f ) = f (xσ 1, xσ 2, . . . , xσ n).
This was the action we used in Chapter 3 to define the parity of a permutation and prove the parity theorem. It has historical interest as well. It is the context in which Lagrange proved Lagrange’s theorem—in essence, what he actually did is prove Theorem 4.40 for this action. Moreover, this is the group action that launched Galois theory, about which we say more in Chapter 11.
