
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index

256 |
13 GEOMETRICAL CONSTRUCTIONS |
where [Q(Xk+1) : Q(Xk )] = 1 or 2 for 2 k m − 1. Furthermore, each extension field Q(Xk ) is a subfield of R because Q and Xk are sets of real numbers. By dropping each field Q(Xi ) that is a trivial extension of Q(Xi−1), it follows that
α Kn Kn−1 · · · K0 = Q |
|
where [Ki : Ki−1] = 2 for 1 i n. |
|
Corollary 13.6. If α is constructible, then [Q(α) : Q] = 2r for some r 0. |
|
Proof. If α is constructible, then α Kn Kn−1 · · · K0 = Q, where Ki is an extension field of degree 2 over Ki−1. By Theorem 11.6,
[Kn : Q(α)][Q(α) : Q] = [Kn : Q]
= [Kn : Kn−1][Kn−1 : Kn−2] · · · [K1 : Q] = 2n.
Hence [Q(α) : Q]|2n; thus [Q(α) : Q] = 2r for some r 0. |
|
Corollary 13.7. If [Q(α) : Q] = 2r for some r 0, then α is not constructible.
Corollary 13.6 does not give a sufficient condition for α to be constructible, as shown in Example 13.17 below.
Example 13.8. Can a root of the polynomial x5 + 4x + 2 be constructed using straightedge and compass?
Solution. Let α be a root of x5 + 4x + 2. By Eisenstein’s criterion, x5 + 4x +
2 is irreducible over Q; thus, by Corollary 11.12, [Q(α) : Q] = 5. Since |
5 is not |
a power of 2, it follows from Corollary 13.7 that α is not constructible. |
|
Example 13.9. Can a root of the polynomial x4 − 3x2 + 1 be constructed using straightedge and compass?
|
Solution. Solving the equation x4 − 3x2 + 1 = 0, we obtain x2 = (3 ± √ |
|
)/2 |
|||
|
5 |
|||||
be |
|
|
|
|
|
|
and x = ± |
|
(3 ± √5)/2. It follows from Theorem 13.5 that all these roots can |
||||
constructed.
DUPLICATING A CUBE
Let l be the length of the sides of a given cube so√that its volume is l3. A cube with double the volume will have sides of length 3 2 l.
√
Proposition 13.10. 3 2 is not constructible.

TRISECTING AN ANGLE |
|
|
|
257 |
||||
3 |
|
|
|
|
|
|
|
(Theo- |
|
|
|
|
|
|
|
||
Proof. √2 is a root of x3 − 2 which, by the rational roots theorem3 |
||||||||
rem 9.25), is irreducible3 over Q. Hence, by Corollary 11.12, [Q( |
√ |
2 |
) : Q] = 3 |
|||||
so, by Corollary 13.7, √ |
|
is not constructible. |
|
|
|
|
||
2 |
|
|
|
|||||
√
Since we cannot construct a length of 3 2 l starting with a length l, the ancient problem of duplicating the cube is insoluble.
TRISECTING AN ANGLE
Certain angles can be trisected using straightedge and compass. For example, π, π/2, 3π/4 can be trisected because π/3, π/6, and π/4 can be constructed. However, we show that not all angles are trisectable by proving that π/3 cannot be trisected.
If we are given the angle φ, we can drop a perpendicular from a point a unit distance from the angle to construct the lengths cos φ and sin φ, as shown in Figure 13.4. Conversely, if either cos φ or sin φ is constructible, it is possible to construct the angle φ. Hence, if we are given an angle φ, we can construct all numbers in the extension field Q(cos φ). Of course, if cos φ Q, then Q(cos φ) = Q.
We can now consider those numbers that are constructible from Q(cos φ). This notion of constructibility is similar to our previous notion, and similar results hold, except that the starting field is Q(cos φ) instead of Q.
Theorem 13.11. The angle φ can be trisected if and only if the polynomial 4x3 − 3x − cos φ is reducible over Q(cos φ).
Proof. Let θ = φ/3. The angle θ can be constructed from φ if and only if cos θ can be constructed from cos φ. It follows from De Moivre’s theorem and the binomial theorem that
cos φ = cos 3θ = 4 cos3 θ − 3 cos θ.
Hence cos θ is a root of f (x) = 4x3 − 3x − cos φ.
If f (x) is reducible over Q(cos φ), then cos θ is a root of a polynomial of degree 1 or 2 over Q(cos φ); thus [Q(cos φ, cos θ ) : Q(cos φ)] = 1 or 2. Hence, by Propositions 11.16 and 13.3, cos θ is constructible from Q(cos φ).
1
sin f
f
cos f
Figure 13.4. Constructing sin φ and cos φ from the angle φ.
258 |
13 |
GEOMETRICAL CONSTRUCTIONS |
If f (x) is |
irreducible over Q(cos φ), then |
[Q(cos φ, cos θ ) : Q(cos φ)] = 3, |
and it follows, by a proof similar to that of Theorem 13.5, that cos θ cannot be
constructed from Q(cos φ) by using straightedge and compass. |
|
|
|||||||||||||||||
Corollary 13.12. If cos φ |
|
Q, then the angle φ |
can be trisected if and only if |
||||||||||||||||
|
3 |
− 3x |
|
|
|
|
|
|
|
|
|
|
|||||||
4x |
|
− cos φ is reducible over Q. |
|
|
|
|
|
||||||||||||
|
3For example, if φ = π/2, then φ can be trisected because the polynomial |
||||||||||||||||||
4x |
|
− 3x + 0 is reducible over Q. |
|
|
|
|
|
|
|||||||||||
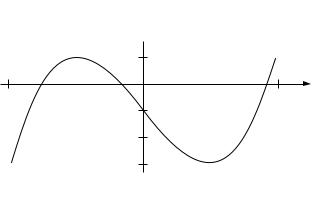
Proposition 13.13. π/3 cannot be trisected by straightedge and compass. |
|
||||||||||||||||||
|
Proof. The polynomial f (x) = 4x3 − 3x − cos(π/3) = 4x3 − 3x − 21 . Now, |
||||||||||||||||||
by |
3the rational roots |
theorem (Theorem 9.25), the only possible roots of 2f (x) |
= |
||||||||||||||||
, |
1 |
, |
|
1 |
|
1 |
|
|
|
|
|||||||||
8x |
|
|
x |
|
|
|
± 2 |
± 4 , or |
± 8 |
. We see from the |
graph of f (x) in Fig- |
||||||||
|
|
− 6 |
− 1 are ±1 |
|
1 |
1 |
|
||||||||||||
ure |
13.5 that none of these are roots, except possibly |
− 4 or |
− 8 . However, |
||||||||||||||||
|
1 |
3 |
|
|
1 |
|
|
17 |
|
|
|
|
|||||||
f (− |
4 ) = |
|
|
and f (− |
8 ) = − |
|
; thus f (x) has no rational roots. Hence f (x) is |
||||||||||||
|
16 |
128 |
|||||||||||||||||
irreducible over Q, and by Corollary 13.12, π/3 cannot be trisected by straightedge and compass.
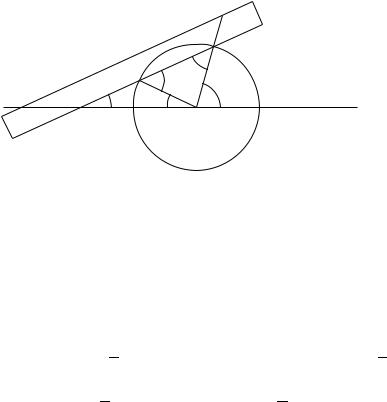
Example 13.14. Archimedes showed that, if we are allowed to mark our straightedge, it is possible to trisect any angle.
Construction. Let AOB be the angle φ we are to trisect. Draw a circle with center O and any radius r and let this circle meet OA and OB in P and Q. Mark two points X and Y on our straightedge of distance r apart. Now move this straightedge through Q, keeping X on OA until Y lies on the circle, as shown in Figure 13.6. Then we claim that the angle OXY is φ/3, and hence the angle AOB is trisected.
Solution. Let angle OXY = θ . Since triangle XYO is isosceles, the angle XOY = θ . Now
angle OYQ = angle OXY + angle XOY = 2θ.
 f(x)
f(x)
−1 |
0 |
1 |
x |
|
−1
Figure 13.5. Graph of f (x) = 4x3 − 3x − 12 .
CONSTRUCTING REGULAR POLYGONS |
259 |
 B
B
2q Q
Y
|
|
r |
2q |
|
|
|
|
|
|
|
|
|
|
X |
q |
|
q |
f |
|
|
|
|
|
O |
r |
P |
A |
Figure 13.6. Trisection of the angle φ using a marked ruler.
Triangle YOQ is isosceles, so angle OQY = 2θ . Also,
φ = angle AOB = angle OXQ + angle OQX = θ + 2θ = 3θ.
Hence θ = φ/3.
SQUARING THE CIRCLE
Given any circle of radius r, its area is π r2, so that a square with the same
√ √
area has sides of length π r. We can square the circle if and only if π is constructible.
√ √
Proposition 13.15. [Q( π ) : Q] is infinite, and hence π is not constructible.
Proof. The proof of this depends on the fact that π is transcendental over Q; that is, π does not satisfy any polynomial equation with rational coefficients. This was mentioned in Chapter 11, and a proof is given in Stewart [35].
2 3 |
|
|
= |
|
|
|
|
|
|
|
Q(π ) is a subfield of Q(√π ) because π |
|
(√π )2 |
|
Q(√π ). Since π is tran- |
||||||
scendental, π, π , π , . . . are linearly independent over Q, and [Q(π ) : Q] is infinite. Therefore,
[ |
( |
π |
) : |
Q |
] = [ ( |
π |
) : |
Q |
(π )][ (π ) : |
] |
|
|
Q |
√ |
Q √ |
|
Q |
Q |
|
||||||
is also infinite. Hence, by Corollary 13.7, |
√ |
|
is not constructible. |
|
||||||||
π |
||||||||||||
Hence the circle cannot be squared by straightedge and compass.
CONSTRUCTING REGULAR POLYGONS
Another problem that has been of great interest to mathematicians from the time of the ancient Greeks is that of constructing a regular n-gon, that is, a regular polygon with n sides. This is equivalent to constructing the angle 2π/n or the
