
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index

EXERCISES |
233 |
EXERCISES
For Exercises 11.1 to 11.4, write out the addition and multiplication tables for the fields.
11.1. |
GF(5). |
11.2. |
GF(7). |
11.3. |
GF(9). |
11.4. |
GF(8). |
For Exercises 11.5 to 11.10, in each case find, if possible, an irreducible polynomial of degree n over F .
11.5. |
n = 3, F = Z11. |
11.6. |
n = 3, F = Q. |
11.7. |
n = 4, F = R. |
11.8. |
n = 3, F = GF(4). |
11.9. |
n = 2, F = Q(i). |
11.10. |
n = 5, F = Z3. |
For Exercises 11.11 to 11.13, in each case, find a polynomial in F [x] with r as a root.
11.11.r = √2 + √6, F = Q.
11.12.r = π + ei, F = R.
√√
11.13.r = 3 3/ 2, F = Q.
11.14.Show that θ = 2kπ/7 satisfies the equation cos 4θ − cos 3θ = 0 for each integer k. Hence find an irreducible polynomial over Q with cos(2π/7) as a root.
11.15.Prove that the algebraic numbers
A = {x C|x is algebraic over Q}
form a subfield of C.
11.16.Assuming the fundamental theorem of algebra, prove that every polynomial in A has a root in A.
For Exercises 11.17 to 11.25, Calculate the degrees.
3 |
|
|
11.18. [C : Q]. |
|
|
||
11.17. [Q(√7) : Q]. |
|
|
|||||
11.19. [Q(i, 3i) : Q]. |
√ |
|
|
||||
11.20. [C : R( |
−7)]. |
||||||
11.21. [Z3[x]/(x2 + x + 2) : Z3]. |
11.22. [Q(i, √ |
|
) : Q]. |
||||
2 |
|||||||
11.23. [A : Q]. |
11.24. [C : A]. |
|
|
||||
11.25. [Z3(t) : Z3], where Z3(t) is the field of rational functions in t over Z3. |
|||||
11.26. Prove that x |
2 |
− 2 is irreducible over Q( |
√ |
|
|
|
|||||
|
3). |
||||
For Exercises 11.27 to 11.32, find the inverses of the elements in the given fields. Each field is a finite extension F (α). Express your answers in the form a0 + a1 α +
√, where√ai F and [F (α) : F ] = n.
11.27.1 + 3 2 in Q( 3 2).
√√ √
11.28.4 5 + 5 in Q( 4 5).
11.29.5 + 6ω in Q(ω), where ω is a complex cube root of 1.−· · · +

234 |
11 FIELD EXTENSIONS |
11.30.2 − 3i in Q(i).
11.31.α in GF(32) = Z2(α), where α5 + α2 + 1 = 0.
11.32.α in GF(27) = Z3(α), where α3 + α2 + 2 = 0.
For Exercises 11.33 to 11.40, find the characteristic of the rings. Which of these are fields?
11.33. Z2 × Z2. |
11.34. Z3 × Z4. |
|||
11.35. GF(49). |
11.36. Z × Z2. |
|||
11.37. |
3 |
|
|
11.38. M2(Z5). |
Q(√7). |
||||
11.39. |
Q × Z3. |
11.40. GF(4)[x]. |
||
11.41.Let R be any ring and n a positive integer. Prove that In = {na|a R} is an ideal of R and that the characteristic of R/In divides n.
11.42.Let M be a finite subgroup of the multiplicative group F of any infinite
field F . Prove that M is cyclic, and give an example to show that F need not be cyclic.
11.43.For what values of m is (Zm, ·) cyclic? (This is a difficult problem; see Exercises 4.55 to 4.62 for other results on Zm.)
11.44.Let GF(4) = Z2(α), where α2 + α + 1 = 0. Find an irreducible quadratic in GF(4)[x]. If β is the root of such a polynomial, show that GF(4)(β) is a Galois field of order 16.
11.45.(a) Show that there are (p2 − p)/2 monic irreducible polynomials of degree 2 over GF(p). (A polynomial is monic if the coefficient of the highest power of the variable is 1.)
(b)Prove that there is a field with p2 elements for every prime p.
11.46.(a) How many monic irreducible polynomials of degree 3 are there over
GF(p)?
(b)Prove that there is a field with p3 elements for every prime p.
√√−3) = Q(α).11.47. Find an element α such that
11.48. Find all primitive elements in GF(16) = Z2(α), where α4 + α + 1 = 0.
11.49. Find all the primitive elements in GF(32).
For Exercises 11.50 and 11.51, find a primitive polynomial of degree n over the field F.
11.50. n = 2, F = Z5. |
11.51. n = 3, F = Z2. |
|
|
|
||||||||
11.52. Let |
|
m |
|
be a polynomial |
of degree |
m |
over |
Z |
p . If g(x)|(x |
k |
− 1) |
for |
|
g(x) |
|
|
|
|
|
|
|
||||
k = p |
|
− 1 and for no smaller k, show that g(x) is irreducible over Zp . |
||||||||||
11.53.Prove that x8 + x Z2[x] will split into linear factors over GF(8) but not over any smaller field.
11.54.Let f (x) = 2x3 + 5x2 + 7x + 6 Q[x]. Find a field, smaller than the complex numbers, in which f (x) splits into linear factors.
11.55.If α and β are roots of x3 + x + 1 and x3 + x2 + 1 Z2[x], respectively, prove that the Galois fields Z2(α) and Z2(β) are isomorphic.
EXERCISES |
235 |
11.56.(a) If p(x) Z2[x], prove that [p(x)]2 = p(x2).
(b)If β is a root of p(x) Z2[x], prove that β2l is a root for all l N.
(c)Let GF(16) = Z2(α) where α4 + α + 1 = 0. Find an irreducible polynomial in Z2[x] with α3 as a root.
For Exercises 11.57 and 11.58, |
solve the simultaneous linear equations in |
GF(4 ) = Z2 (α). |
11.58. (α + 1)x + y = α |
11.57. αx + (α + 1)y = α + 1 |
|
x + αy = 1. |
x + (α + 1)y = α + 1. |
11.59.Solve the quadratic equation αx2 + (1 + α)x + 1 = 0 over the field
GF(4) = Z2(α).
11.60.Let R be any commutative ring of characteristic p, where p is a prime.
(a) Show that (a + b)p = ap + bp for all a, b in R. [Hint: If |
p |
r |
denotes the binomial coefficient, show that
whenever 1 r p.]
(b) If σ : R → R is defined by σ (a) = ap for all a ring morphism.
r |
= r |
r |
− |
1 |
|
p |
p |
p |
|
1 |
|
−
a R, show that σ is
(c)If R = GF(pn) show that σ is an isomorphism of R (called the Frobenius automorphism).
11.61.If F is a field and F is cyclic, show that F is finite.
11.62.Design a feedback shift register using six delays that has a cycle length of 63.
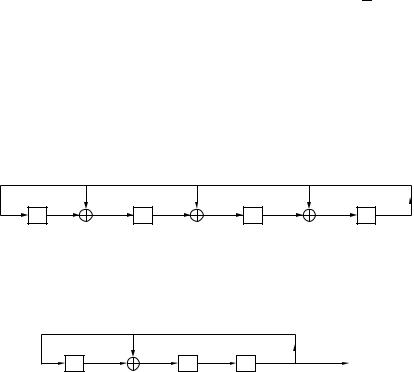
11.63.What is the cycle length of the feedback shift register in Figure 11.3?
Figure 11.3
11.64.Design a feedback shift register that has a cycle length of 21.
11.65.Describe the output sequence of the feedback shift register in Figure 11.4 when the registers initially contain the elements shown.
1 |
0 |
1 |
Output
Figure 11.4
11.66.If a feedback shift register with n delays has a cycle length of 2n − 1, show that the feedback connections must be derived from a primitive irreducible polynomial of degree n over Z2.

12
LATIN SQUARES
Latin squares first arose with parlor games such as the problem of arranging the jacks, queens, kings, and aces of a pack of cards in a 4 × 4 array so that each row and each column contains one card from each suit and one card from each rank. In 1779, Leonard Euler posed the following famous problem of the 36 officers from six ranks and six regiments. He claimed that it was impossible to arrange these officers on parade in a 6 × 6 square so that each row and each column contains one officer from each rank and one from each regiment.
Recently, statisticians have found latin squares useful in designing experiments, and mathematicians have found close connections between latin squares and finite geometries.
LATIN SQUARES
Let S be a set with n elements. Then a latin square L = (lij ), of order n based on S, is an n × n array of the elements of S such that each element appears exactly once in each row and once in each column.
For example, Table 12.1 illustrates a latin square of order 3 based on {a, b, c}.
Theorem 12.1. The table for any finite group (G, +) of order n is a latin square of order n based on G.
Proof. We write the operation in G as addition, even though the result still
holds if G is not commutative. |
row are equal. Then xi + xj = xi + xk |
Suppose that two elements in one |
|
for some xi , xj , xk G. Since G is |
a group, xi has an inverse (−xi ) such |
that (−xi ) + xi = 0. Hence (−xi ) + (xi + xj ) = (−xi ) + (xi + xk ), and since the |
|
operation is associative, we have xj = xk . Therefore, an element cannot appear twice in the same row. Similarly, an element cannot appear twice in the same column, and the table is a latin square.
Modern Algebra with Applications, Second Edition, by William J. Gilbert and W. Keith Nicholson ISBN 0-471-41451-4 Copyright 2004 John Wiley & Sons, Inc.
LATIN SQUARES |
|
237 |
||
|
TABLE 12.1. Latin |
|||
|
Square |
|
|
|
|
|
|
|
|
|
a |
b |
c |
|
|
c |
a |
b |
|
|
b |
c |
a |
|
|
|
|
|
|
TABLE 12.2. Latin Squares of Order 4 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
(0, 0) |
(0, 1) |
(1, 0) |
(1, 1) |
|
c |
b |
a |
d |
||||
(0, 1) |
(0, 0) |
(1, 1) |
(1, 0) |
|
d |
a |
b |
c |
||||
(1, |
0) |
(1, |
1) |
(0, |
0) |
(0, |
1) |
|
a |
d |
c |
b |
(1, |
1) |
(1, |
0) |
(0, |
1) |
(0, |
0) |
|
b |
c |
d |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
Given any latin square, we can permute the rows among themselves and also the columns among themselves and we still have a latin square. For example, the addition table for Z2 × Z2 is a latin square of order 4. If we interchange the first and third columns and replace (0, 0) by a, (0, 1) by b, (1, 0) by c, and (1, 1) by d, we obtain another latin square of order 4 based on {a, b, c, d}. These are illustrated in Table 12.2.
Latin squares are useful in designing statistical experiments because they can show how an experiment can be arranged so as to reduce the errors without making the experiment too large or too complicated. See Laywine and Mullen [40] for more complete details.
Suppose that you wanted to compare the yields of three varieties of hybrid corn. You have a rectangular test plot, but you are not sure that the fertility of the soil is the same everywhere. You could divide up the land into nine rectangular regions and plant the three varieties, a, b, and c, in the form of the latin square in Table 12.1. Then if one row were more fertile than the others, the latin square would reduce the error that this might cause. In fact, if the soil fertility was a linear function of the coordinates of the plot, the latin square arrangement would minimize the error.
Of course, the error could be reduced by subdividing the plot into a large number of pieces and planting the varieties at random. But this would make it much more difficult to sow and harvest.
Example 12.2. A smoking machine is used to test the tar content of four brands of cigarettes; the machine has four ports so that four cigarettes can be smoked simultaneously. However, the four ports might not be identical and that might affect the measurements of the tar content. Also, if four runs were made on the machine, testing one brand at a time, the humidity could change, thus affecting the results.
Show how to reduce the errors due to the different ports and the different runs by using a latin square to design the experiment.
