190 9 POLYNOMIAL AND EUCLIDEAN RINGS

If m < n, we would obtain the relation pm+1 · · · pn = u1u2 · · · um, which is impossible because irreducibles cannot divide an invertible element. If m > n,

we would obtain

1 = u1u2 · · · unqn+1 · · · qm,

which is again impossible because an irreducible cannot divide 1. Hence m = n, and the primes p1, p2, . . . , pn are the same as q1, q2, . . . , qm up to a rearrangement and up to multiplication by invertible elements.

When the euclidean ring is the integers, the theorem above yields the fundamental theorem of arithmetic referred to earlier. The ring of polynomials over a field and the gaussian integers also have this unique factorization property enjoyed by the integers. However, the integral domain

Z[√−3] = {a + b√−3 |a, b Z},

which is a subring of C, does not have the unique factorization property. For example,

whereas 2, 1 + √−3, and 1 − √−3 are all irreducible. Therefore, Z[√−3] cannot be a euclidean ring.

FACTORING REAL AND COMPLEX POLYNOMIALS

The question of whether or not a polynomial is irreducible will be crucial in Chapter 10 when we extend number fields by adjoining roots of a polynomial. We therefore investigate different methods of factoring polynomials over various coefficient fields.

A polynomial f (x) of positive degree is said to be reducible over the field F if it can be factored into two polynomials of positive degree in F [x]. If it cannot be so factored, f (x) is called irreducible over F , and f (x) is an irreducible element of the ring F [x]. It is important to note that reducibility depends on the field F . The polynomial x2 + 1 is irreducible over R but reducible over C.

The following basic theorem, first proved by Gauss in his doctoral thesis in 1799, enables us to determine which polynomials are irreducible in C[x] and in R[x].

Theorem 9.21. Fundamental Theorem of Algebra. If f (x) is a polynomial in

C[x] of positive degree, then f (x) has a root in C.

A proof of this theorem is given in Nicholson [11] using the fact from analysis that a cubic real polynomial has a real root.

The following useful theorem shows that the complex roots of real polynomials occur in conjugate pairs.

Theorem 9.22. (i) If z = a + ib is a complex root of the real polynomial f (x)

Proof. (i) Let g(x) = x2 − 2ax + a2 + b2 = (x − z)(x − z). By the division algorithm in R[x], there exist real polynomials q(x) and r(x) such that

f (x) = q(x)g(x) + r(x) where r(x) = 0 or deg r(x) < 2.

Hence r(x) = r0 + r1x where r0, r1 R. Now z = a + ib is a root of f (x) and of g(x); therefore, it is also a root of r(x), so 0 = r0 + r1(a + ib). Equating real and imaginary parts, we have r0 + r1a = 0 and r1b = 0. But then

r(z) = r(a − ib) = r0 + r1(a − ib) = r0 + r1a − ir1b = 0.

Since z is a root of r(x) and g(x), it must be a root of f (x).

If z is complex and not real, then b = 0. In this case r1 = 0 and r0 = 0; thus

Theorem 9.23. (i) The irreducible polynomials in C[x] are the polynomials of degree 1.

(ii) The irreducible polynomials in R[x] are the polynomials of degree 1

Proof. (i) The polynomials of degree 0 are the invertible elements of C[x]. By the fundamental theorem of algebra, any polynomial of positive degree has a root in C and hence a linear factor. Therefore, all polynomials of degree greater than 1 are reducible and those of degree 1 are the irreducibles.

can be factored into linear factors in C[x]. By Theorem 9.22 (i), its nonreal roots fall into conjugate pairs, whose corresponding factors combine to give a quadratic factor in R[x] of the form ax2 + bx + c, where b2 < 4ac. Hence any real polynomial can be factored into real linear factors and real quadratic factors

FACTORING RATIONAL AND INTEGRAL POLYNOMIALS

A rational polynomial can always be reduced to an integer polynomial by multiplying it by the least common multiple of the denominators of its coefficients. We now give various methods for determining whether an integer polynomial has rational roots or is irreducible over Q.

Theorem 9.25. Rational Roots Theorem. Let p(x) = a0 + a1x + · · · + anxn

Z[x]. If r/s is a rational root of p(x) and gcd(r, s) = 1, then:

(i)r|a0.

(ii)s|an.

Proof. If p(r/s) = 0, then a0 + a1(r/s) + · · · + an−1(r/s)n−1 + an(r/s)n =

0, whence a0sn + a1rsn−1 + · · · + an−1rn−1s + anrn = 0. Therefore, a0sn =

Solution. If p(r/s) = 0, then, by Theorem 9.25, r|(−1) and s|2. Hence r =

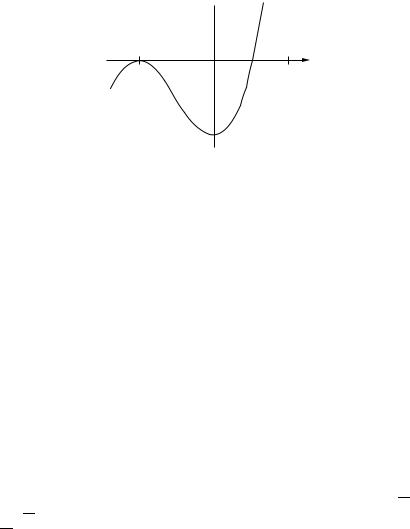
±1 and s = ±1 or ±2, and the only possible values of r/s are ±1, ±1/2. Instead of testing all these values, we sketch the graph of p(x) to find approximate roots. Differentiating, we have p (x) = 6x2 + 6x = 6x(x + 1), so p(x) has turning values at 0 and −1.

194 9 POLYNOMIAL AND EUCLIDEAN RINGS

Now p|c0, p|c1, . . . , p|cj −1, p|bi−1, p|bi−2, . . . , p|b0 but p |bi cj so this coefficient is not divisible by p. Hence the greatest common divisor of the coefficients of Q(x)R(x) is 1; therefore, uv|st and P (x) can be factored in Z[x].

Example 9.29. Factor p(x) = x4 − 3x2 + 2x + 1 into irreducible factors in Q[x].

Solution. By Theorem 9.25, the only possible rational roots are ±1. However, these are not roots, so p(x) has no linear factors.

Therefore, if it does factor, it must factor into two quadratics, and by Gauss’ lemma these factors can be chosen to have integral coefficients. Suppose that

x4 − 3x2 + 2x + 1 = (x2 + ax + b)(x2 + cx + d)

=x4 + (a + c)x3 + (b + d + ac)x2 + (bc + ad)x + bd.

Thus we have to solve the following system for integer solutions:

a + c = 0, b + d + ac = −3, bc + ad = 2, and bd = 1.

Therefore, b = d = ±1 and b(a + c) = 2. Hence a + c = ±2, which is a contradiction. The polynomial cannot be factored into two quadratics and therefore

Z[x]. Suppose that the following conditions all hold for some prime p:

(i)p|a0, p|a1, . . . , p|an−1.

(ii)p |an.

(iii)p2 |a0.

Then f (x) is irreducible over Q.

Proof. Suppose that f (x) is reducible. By Gauss’ lemma, it factors as two polynomials in Z[x]; that is,

f (x) = (b0 + · · · + br xr )(c0 + · · · + cs xs ),

where bi , cj Z, s > 0, and r + s = n. Comparing coefficients, we see that a0 = b0c0. Now p|a0, but p2 |a0, so p must divide b0 or c0 but not both. Without loss of generality, suppose that p|b0 and p |c0. Now p cannot divide all of b0, b1, . . . , br , for then p would divide an. Let t be the smallest integer for which p |bt ; thus 1 t r < n. Then at = bt c0 + bt −1c1 + · · · + b1ct −1 + b0ct and p|at , p|b0, p|b1, . . . , p|bt −1. Hence p|bt c0. However, p |bt and p |c0, so we have a contradiction, and the theorem is proved.