
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index

130 |
´ |
6 POLYA–BURNSIDE METHOD OF ENUMERATION |
g1 |
g2 |
g3 |
Figure 6.5. Types of rotations of a dodecahedron.
TABLE 6.5. Colorings of the Dodecahedron
Type of Element, gi |
|
Number, s, of |
|Fix gi | |
s · |Fix gi | |
||
(Figure 6.5) |
Order of gi |
Such Elements |
||||
Identity |
1 |
|
|
1 |
792 |
792 |
g1 |
2 |
|
· 2 |
15 |
0 |
0 |
g2 |
3 |
10 |
= 20 |
0 |
0 |
|
g3 |
5 |
6 |
· 4 |
= 24 |
2 |
48 |
|
|
|A5| = 60 |
|
= 840 |
||
COUNTING SWITCHING CIRCUITS
The Burnside theorem can still be applied when the sets to be enumerated do not have any geometric symmetry. In this case, the symmetry group is usually the full permutation group Sn.
Consider the different switching circuits obtained by using three switches. We can think of these as black boxes with three binary inputs x1, x2, and x3 and one binary output f (x1, x2, x3), as in Figure 6.6. Two circuits, f and g, are called equivalent if there is a permutation π of the variables so that f (x1, x2, x3) = g(xπ 1, xπ 2, xπ 3). Equivalent circuits can be obtained from each other by just permuting the wires outside the black boxes, as in Figure 6.7.
x1 |
|
|
|
|
f(x1, x2, x3) |
|
|
|
|||
x2 |
|
|
f |
|
|
|
|
||||
x3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Figure 6.6. |
Switching circuit. |
|
|||
|
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
f |
|
|
f(x2, x3, x1) |
|
|
|
|||
x3 |
|
|
|
|
|
Figure 6.7. Permutation of the inputs.
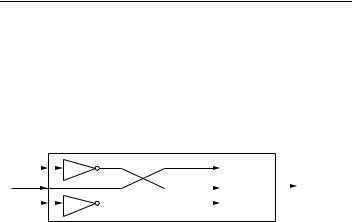
COUNTING SWITCHING CIRCUITS |
131 |
Example 6.6. Find the number of switching circuits using three switches that are not equivalent under permutations of the inputs.
Solution. There are eight possible inputs using three binary variables and hence there are 28 = 256 circuits to consider. The symmetric group S3 acts on these 256 circuits, and we wish to find the number of different equivalence classes, that is, the number of orbits.
Table 6.6 lists the number of circuits left fixed by the different types of elements in S3. For example, if the switching function f (x1, x2, x3) is fixed by
the |
transposition |
(12) of |
the input variables, then f (0, 1, 0) = f (1, 0, 0) and |
|||||||||||
f ( |
, |
|
, |
|
) |
= |
f ( , |
, |
) |
|
f |
(0, 0, 1), (0, 1, |
||
0 |
|
1 |
|
1 |
|
1 |
0 |
1 . The values of |
|
for the inputs (0, 0, 0), |
6 |
ways. |
||
0), (0, 1, 1), (1, 1, 0), and (1, 1, 1) can be chosen arbitrarily in 2 |
|
|||||||||||||
By Burnside’s theorem and Table 6.6, the number of nonequivalent circuits is 480/|S3| = 480/6 = 80.
However, this number can be reduced further if we allow permutations and complementation of the three variables. In a circuit consisting of two-state switches, the variable xi can be complemented by simply reversing each of the switches controlled by xi . The resulting circuit is just as simple and the cost is the same as the original one. In transistor networks, we can just permute the input wires and add NOT gates as in Figure 6.8.
The eight input values of a three-variable switching circuit can be considered as the vertices of a three-dimensional cube, as shown in Figure 6.9. The six faces of this cube are defined by the equations x1 = 0, x1 = 1, x2 = 0, x2 = 1, x3 = 0, x3 = 1. The group that permutes and complements the variables takes each face to another face and takes opposite faces to opposite faces. Hence the group is the complete symmetry group, G, of the cube. There is a morphism ψ : G → {1, −1},
TABLE 6.6. Action of S3 on the Inputs of the Switches
|
Type of Element, |
Number, s, of |
|
|
|Fix g| |
s · |Fix g| |
||||||||||
|
g S3 |
|
|
Such Elements |
|
|
||||||||||
|
Identity |
|
|
1 |
|
8 |
|
8 |
= 256 |
|
||||||
|
|
|
|
26 |
|
26 |
|
|||||||||
|
Transposition |
3 |
|
24 |
|
3 · 24 |
= 192 |
|
||||||||
|
3-Cycle |
|
|
2 |
|
2 |
|
2 · 2 |
|
= |
32 |
|
||||
|
|
|
|
|
|
|S3| = 6 |
|
|
|
|
|
|
480 |
|
||
x1 |
|
NOT |
|
|
|
|
|
|
|
|
, x ′, x ′) |
|||||
|
|
|
|
|
f |
|
f(x |
|
||||||||
x |
2 |
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|||
x3 |
|
NOT |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Figure 6.8. Permutation and complementation of inputs.

132 |
´ |
6 POLYA–BURNSIDE METHOD OF ENUMERATION |
111
011 |
101 |
110 |
|
|
|
001 |
010 |
100 |
|
000
Figure 6.9. Cube of input values.
which sends proper rotations to 1 and improper rotations to −1; the kernel of ψ is the group of proper rotations of the cube which, by the morphism theorem, must be a normal subgroup of index 2. Therefore, the order of G is 2 · 24 = 48.
Example 6.7. Find the number of switching circuits involving three switches that are nonequivalent under permutation and complementation of the variables.
Solution. Each boolean function in three variables defines a coloring of the vertices of the cube of input values. A vertex is colored black if the function is 1 for the corresponding input value. It is colored white if the function takes the value 0 at that input value.
We can represent the complete symmetry group, G, of the cube by means of permutations of the vertices labeled 0, 1, 2, 3, 4, 5, 6, 7 in Figure 6.10. Since the group of proper rotations of the cube is a normal subgroup of index 2 in G, every element of G can be written as a proper rotation π or as π Ž ρ, where ρ is the reflection of the cube in its center.
There are 28 different switching functions of three variables, and Table 6.7 describes the number of circuits that are fixed by the action of each element of the group G on the eight inputs. For example, consider the element g = (01) Ž (67) Ž (34) Ž (25). If a switching function f is fixed under the action of g, then the images of the input values corresponding to the vertices 0 and 1 must be the same; that is, f (0, 0, 0) = f (0, 0, 1). Similarly, the images of the input values corresponding to the vertices 6 and 7 are the same, and f (1, 1, 0) = f (1, 1, 1).
7 |
3 |
6 |
|
5 |
|
2 |
1 |
4 |
0 |
Figure 6.10. Labeling of the cube.
COUNTING SWITCHING CIRCUITS |
|
|
|
|
|
133 |
TABLE 6.7. Symmetries of a Cube Acting on the Three-Variable |
|
|
|
|||
Switching Functions |
|
|
|
|
|
|
|
|
|
|
|
|
|
Type of Element, |
|
|
|
|
|
|
g, in the Symmetry |
|
Number, s, of |
|Fix g| |
s · |Fix g| |
||
Group of the Cube |
Order of g Such Elements |
|||||
Proper rotations |
|
|
|
|
|
|
Identity |
1 |
1 |
|
28 |
256 |
|
Rotation about a line joining |
2 |
6 |
|
24 |
96 |
|
midpoints of opposite edges |
|
|
|
|
|
|
[e.g., (01) Ž (67) Ž (34) Ž (25)] |
|
|
|
24 |
|
|
Rotation about a line joining |
3 |
8 |
|
128 |
||
opposite vertices |
|
|
|
|
|
|
[e.g., (124) Ž (365) Ž (0) Ž (7)] |
|
|
|
22 |
|
|
Rotation about a line joining centers |
4 |
6 |
|
24 |
||
of opposite faces |
|
|
|
|
|
|
[e.g., (0264) Ž (1375)] |
|
|
|
24 |
|
|
Rotation about a line joining centers |
2 |
3 |
|
48 |
||
of opposite faces |
|
|
|
|
|
|
[e.g., (06) Ž (24) Ž (17) Ž (35)] |
|
|
|
|
|
|
Improper rotations |
|
|
|
|
|
|
Reflection in the center |
2 |
1 |
|
24 |
16 |
|
[ρ = (07) Ž (16) Ž (25) Ž (34)] |
2 |
6 |
|
2 |
6 |
384 |
Reflection in a diagonal plane |
|
|
||||
[e.g., (01) Ž (67) Ž (34) Ž (25) Ž ρ = |
|
|
|
|
|
|
(06) Ž (17) Ž (2) Ž (3) Ž (4) Ž (5)] |
6 |
8 |
|
22 |
|
|
Reflection and rotation |
|
32 |
||||
[e.g., (124) Ž (365) Ž ρ = |
|
|
|
|
|
|
(07) Ž (154623)] |
|
|
|
22 |
|
|
Reflection and rotation |
4 |
6 |
|
24 |
||
[e.g., (0264) Ž (1375) Ž ρ = |
|
|
|
|
|
|
(0563) Ž (1472)] |
|
|
|
24 |
|
|
Reflection in a central plane |
2 |
3 |
|
48 |
||
[e.g., (06) Ž (24) Ž (17) Ž (35) Ž ρ = |
|
|
|
|
|
|
(01) Ž (23) Ž (45) Ž (67)] |
|
|
|
|
|
|
|
|
|G| = 48 |
|
|
1056 |
|
Also, f (0, 1, 1) |
= |
f (1, 0, 0) and f (0, 1, 0) |
= |
f (1, 0, 1). Hence the values |
of |
|
|
|
|
2 |
4 |
||
f (0, 0, 0), f (1, 1, 0), f (0, 1, 1), and f (0, 1, 0) can be chosen arbitrarily in |
|
|||||
ways, and |Fix g| = 24. In general, if the function f is fixed under g, the images of the input values, corresponding to the vertices in any one cycle of g, must be the same. Hence |Fix g| is 2r , where r is the number of disjoint cycles in the permutation representation of g.
It follows from Table 6.7 and the Burnside theorem that the number of nonequivalent circuits is 1056/|G| = 1056/48 = 22.

134 |
|
´ |
|
|
|
|
6 POLYA–BURNSIDE METHOD OF ENUMERATION |
||||
TABLE 6.8. Number of Types of Switching Functions |
|
|
|||
|
|
|
|
|
|
Number of Switches, n |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Number of boolean |
4 |
16 |
256 |
65,536 |
4,294,967,296 |
functions, 22n |
|
|
|
|
|
Nonequivalent functions |
4 |
12 |
80 |
3,984 |
37,333,248 |
under permutations of |
|
|
|
|
|
inputs |
|
|
|
|
|
Nonequivalent functions |
3 |
6 |
22 |
402 |
1,228,158 |
under permutation and |
|
|
|
|
|
complementation of |
|
|
|
|
|
inputs |
|
|
|
|
|
Nonequivalent functions |
2 |
4 |
14 |
222 |
616,126 |
under permutation and |
|
|
|
|
|
complementation of inputs and outputs
We can reduce this number slightly more by complementing the function as well as the variables; this corresponds to adding a NOT gate to the output. The group acting is now a combination of a cyclic group of order 2 with the complete symmetry groups of the cube.
The numbers of nonequivalent circuits for five or fewer switches given in Table 6.8 can be computed as in Example 6.7.
In 1951, the Harvard Computing Laboratory laboriously calculated all the nonequivalent circuits using four switches and the best way to design each of them. It was not until later that it was realized that the Polya´ theory could be applied to this problem.
In many examples, it is quite difficult to calculate |Fix g| for every element g of the group G. Polya’s´ most important contribution to this theory of enumeration was to show how |Fix g| can be calculated, using what are called cycle index polynomials. This saves much individual calculation, and the results on nonequivalent boolean functions in Table 6.8 can easily be calculated. However, it is still a valuable exercise to tackle a few enumeration problems without using cycle index polynomials, since this gives a better understanding of the Polya´ theory. For example, we see in Tables 6.3, 6.4, and 6.7 that |Fix g| is always of the form nr , where r is the number of disjoint cycles in g.
Further information on the Polya´ theory can be obtained from Biggs [15], Lidl and Pilz [10], or Stone [22].
