
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index

126 |
´ |
6 POLYA–BURNSIDE METHOD OF ENUMERATION |
NECKLACE PROBLEMS
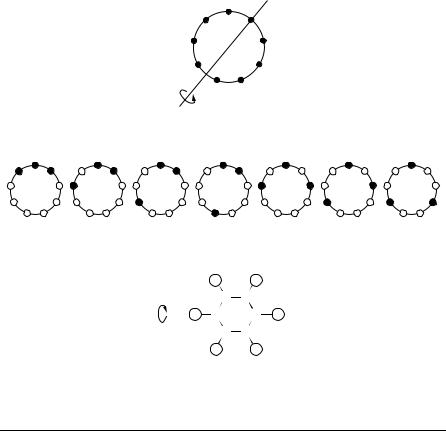
Example 6.2. Three black and six white beads are strung onto a circular wire. This necklace can be rotated in its plane, and turned over. How many different types of necklaces can be made assuming that beads of the same color are indistinguishable?
Solution. Position the three black and six white beads at the vertices of a regular 9-gon. If the 9-gon is fixed, there are 9 · 8 · 7/3! = 84 different ways of doing this. Two such arrangements are equivalent if there is an element of the symmetry group of the regular 9-gon, D9, which takes one arrangement into the other. The group D9 permutes the different arrangements, and the number of nonequivalent arrangements is the number, N , of orbits under D9. We can now use the Burnside theorem to find N .
Table 6.2 lists all the different types of elements of D9 and the number of fixed points for each type. For example, consider the reflection g D9 about the line joining vertex 2 to the center of the circle, which is illustrated in Figure 6.1. Then the arrangements that are fixed under g occur when the black beads are at vertices 1 2 3, 9 2 4, 8 2 5, or 7 2 6. Hence |Fix g| = 4. There are nine reflections about a line, one through each vertex. Therefore, the total number of fixed points contributed by these types of elements is 9 · 4 = 36. A rotation of order 3 in D9 will fix an arrangement if the black beads are at vertices 1 4 7, 2 5 8, or 3 6 9; hence there are three arrangements that are fixed. If an arrangement is fixed under a rotation of order 9, all the beads must be the same color; hence |Fix g| = 0 if g has order 9. Table 6.2 shows that the sum of all the numbers of
fixed points is 126. By Theorem 6.1, N = |
1 |
g D9 |Fix g| = |
126 |
= 7, and |
|D9| |
18 |
|||
there are seven different types of necklaces. |
|
|
|
|
In this example, it is easy to determine all the seven types. They are illustrated in Figure 6.2.
TABLE 6.2. Action of D9 on the Necklaces
Type of Element, |
|
Number, s, of |
|Fix g| |
s · |Fix g| |
g D9 |
Order of g |
Such Elements |
||
Identity |
1 |
1 |
84 |
84 |
Reflection about a line |
2 |
9 |
4 |
36 |
Rotation through 2π/3 or 4π/3 |
3 |
2 |
3 |
6 |
Other rotations |
9 |
6 |
0 |
0 |
|
|
|
|
|
|
|
|
|
= 126 |
NECKLACE PROBLEMS |
127 |
9 |
1 |
2 |
|
8 |
3 |
7 |
4 |
g |
6 5 |
Figure 6.1. D9 |
acting on the necklace. |
Figure 6.2. Seven types of necklaces.
5 |
6 |
C |
C |
– – –g– – – – 4 C |
C 1 – – – – |
C |
C |
3 |
2 |
Figure 6.3. Benzene ring.
TABLE 6.3. Action of D6 on the Compounds
Type of Element, |
|
Number, s, of |
|Fix g| |
s · |Fix g| |
g D6 |
Order of g |
Such Elements |
||
Identity |
1 |
1 |
26 |
64 |
Reflection in a line through |
2 |
3 |
24 |
48 |
opposite vertices |
|
|
|
|
[e.g., (26) Ž (35) Ž (1) Ž (4)] |
|
|
23 |
|
Reflection in a line through |
2 |
3 |
24 |
|
midpoints of opposite sides |
|
|
|
|
[e.g., (56) Ž (14) Ž (23)] |
|
|
|
|
Rotation through ±π/3 |
6 |
2 |
2 |
4 |
[e.g., (123456)] |
|
|
22 |
|
Rotation through ±2π/3 |
3 |
2 |
8 |
|
[e.g., (135) Ž (246)] |
2 |
1 |
23 |
8 |
Rotation through π , |
||||
(14) Ž (25) Ž (36) |
|
|
|
|
|
|
|D6| = 12 |
|
= 156 |

128 |
´ |
6 POLYA–BURNSIDE METHOD OF ENUMERATION |
Example 6.3. Find the number of different chemical compounds that can be obtained by attaching CH3 or H radicals to a benzene ring.
Solution. The carbon atoms are placed at the six vertices of a regular hexagon, and there are 26 ways of attaching CH3 or H radicals. The dihedral group D6 acts on these 26 ways, and we wish to find the number of orbits.
Consider a reflection, g, about a line through opposite vertices. The order of g is 2, and there are three such reflections, through the three opposite pairs of vertices. |Fix g| can be determined by looking at Figure 6.3. If a configuration is fixed by g, the radical in place 2 must be the same as the radical in place 6, and also the radicals in places 3 and 5 must be equal. Hence the radicals in places 1, 2, 3, and 4 can be chosen arbitrarily, and this can be done in 24 ways.
The number of configurations left fixed by each element of D6 is given in Table 6.3. To check that we have not omitted any elements, we add the column containing the numbers of elements, and this should equal the order of the group D6. It follows from the Burnside theorem that the number of orbits is 156/|D6| = 156/12 = 13. Hence there are 13 different types of molecules obtainable.
COLORING POLYHEDRA
Example 6.4. How many ways is it possible to color the vertices of a cube if n colors are available?
Solution. If the cube is fixed, the eight vertices can each be colored in n ways, giving a total of n8 colorings. The rotation group of the cube, S4, permutes these colorings among themselves, and the number of orbits is the number of distinct colorings taking the rotations into account. We can calculate the number of orbits using the Burnside theorem.
There are five types of elements in the rotation group of the cube. We take an element g of each type and determine the vertices that must have the same color in order that the coloring be invariant under g.
Figure 6.4 illustrates the different types of rotations; vertices that have to have the same color are shaded in the same way. Table 6.4 gives the number of fixed colorings, with column totals.
By the Burnside theorem, the number of orbits and hence the number of colorings is
|
1 |
|
g S |
|Fix g| = |
1 |
(n8 + 17n4 + 6n2). |
| |
S4 |
| |
24 |
|||
|
4 |
|
|
|
p
g1 |
|
2p/3 |
|
g2 |
p/2 |
p |
g3 |
g4 |
Figure 6.4. Types of rotations of the cube.
COLORING POLYHEDRA |
|
|
129 |
||
TABLE 6.4. Colorings of the Vertices of the Cube |
|
|
|||
|
|
|
|
|
|
Type of |
Order of |
Number, |
Number, |
|Fix gi | |
|
Element, gi |
s, of |
r, of Choices |
Which Is |
s · |Fix gi | |
|
(Figure 6.4) |
gi |
Such Elements |
of Colors |
nr |
|
Identity |
1 |
1 |
8 |
n8 |
n8 |
|
|
6 · 1 = 6 |
|
4 |
4 |
g1 |
2 |
4 |
n4 |
6n4 |
|
g2 |
3 |
4 · 2 = 8 |
4 |
n2 |
8n2 |
g3 |
4 |
3 · 2 = 6 |
2 |
n4 |
6n4 |
g4 |
2 |
3 · 1 = 3 |
4 |
n |
3n |
|
|
|S4| = 24 |
|
|
n8 + 17n4 + 6n2 |
This shows, |
incidentally, that n8 + 17n4 + 6n2 is |
divisible |
by 24 for all |
||
n P. |
|
|
|
|
|
Example 6.5. In how many ways is it possible to color a regular dodecahedron so that five of its faces are black and the other seven are white?
Solution. The number of ways† of choosing five faces of a fixed dodecahedron
|
12 |
|
12 |
· |
11 |
10 |
· |
9 |
· |
8 |
|
to be colored black is |
5 |
= |
|
|
· |
|
|
= 792. |
|||
|
|
|
5! |
|
|
|
|
The different types of elements in the rotation group, A5, of the dodecahedron are shown in Figure 6.5. The numbers of elements of a given type, in Table 6.5, are calculated as follows. An element of order 3 is a rotation about an axis through opposite vertices. Since there are 20 vertices, there are ten such axes. There are two nonidentity rotations of order 3 about each axis; thus the total number of elements of order 3 is 10 · 2 = 20. The elements of orders 2 and 5 can be counted in a similar way.
If g2 A5 is of order 3, we can calculate |Fix g2| as follows. The element g2 does not fix any face and permutes the faces in disjoint 3-cycles. Now five black faces cannot be permuted by disjoint 3-cycles without fixing two faces, so |Fix g2| = 0. Similarly, |Fix g1| = 0 if g1 is a 2-cycle. If g3 is of order 5, then g3 is a rotation about an axis through the centers of two opposite faces, and these two faces are fixed. The other ten faces are permuted in two disjoint 5-cycles; either of these 5-cycles can be black; thus |Fix g3| = 2.
It follows from Table 6.5 and from the Burnside theorem that the number of different colorings is 840/60 = 14.
Any face coloring of the dodecahedron corresponds to a vertex coloring of its dual, the icosahedron.
n |
|
n |
|
|
n! |
|
|
|
† A set of n elements has k |
subsets of k n elements where |
k |
|
= |
|
|
|
is the binomial |
k!(n |
− |
k)! |
||||||
|
|
|
|
|
|
|
|
|
coefficient.
