SUBGROUPS

Proposition 3.8. If H is a subgroup of (G, ·), then (H, ·) is also a group.

Proof. If H is a subgroup of (G, ·), we show that (H, ·) satisfies all the group axioms. The definition above implies that H is closed under the operation; that is, · is a binary operation on H . If a, b, c H , then (a · b) · c = a · (b · c) in (G, ·) and hence also in (H, ·). Since H is nonempty, it contains at least one element, say h. Now h−1 H and h · h−1, which is the identity, is in H . The definition of subgroup implies that (H, ·) contains inverses. Therefore, (H, ·) satisfies all the axioms of a group.

Conditions (i) and (ii) are equivalent to the single condition:

(iii) a · b−1 H for all a, b H .

However, when H is finite, the following result shows that it is sufficient just to check condition (i).

Proposition 3.9. If H is a nonempty finite subset of a group G and ab H for

j − i > 0. Therefore, e H and this equation can be written as e = a(aj −i−1) = (aj −i−1)a. Hence a−1 = aj −i−1, which belongs to H , since j − i − 1 0.

In the group ({1, −1, i, −i}, ·), the subset {1, −1} forms a subgroup because this subset is closed under multiplication. In the group of translations of the plane (Example 3.1), the set of translations in the horizontal direction forms a subgroup because compositions and inverses of horizontal translations are still horizontal translations.

The group Z is a subgroup of Q, Q is a subgroup of R, and R is a subgroup of C. (Remember that addition is the operation in all these groups.)

However, the set N = {0, 1, 2, . . .} of nonnegative integers is a subset of Z but not a subgroup, because the inverse of 1, namely, −1, is not in N. This example shows that Proposition 3.9 is false if we drop the condition that H be finite.

The relation of being a subgroup is transitive. In fact, for any group G, the inclusion relation between the subgroups of G is a partial order relation.

Example 3.10. Draw the poset diagram of the subgroups of the group of symmetries of a rectangle.

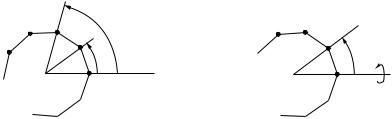
58 3 GROUPS

Proof. From the previous proposition we know that H , the subgroup of G generated by g, has order n. Therefore, H is a subset of the finite set G with the same number of elements. Hence G = H and G is a cyclic group generated by g.

Example 3.15. Show that the Klein 4-group of symmetries of a rectangle, described in Example 3.5, is not cyclic.

Solution. In the Klein 4-group, the identity has order 1, whereas all the other elements have order 2. As it has no element of order 4, it cannot be cyclic.

All the elements of the Klein 4-group can be written in terms of a and b. We therefore say that this group can be generated by the two elements a and b.

Example 3.16. Show that the group of proper rotations of a regular n-gon in the plane is a cyclic group of order n generated by a rotation of 2π/n radians. This group is denoted by Cn.

Solution. This is the group of those symmetries of the regular n-gon that can be performed in the plane, that is, without turning the n-gon over.

Label the vertices 1 through n as in Figure 3.4. Under any symmetry, the center must be fixed, and the vertex 1 can be taken to any of the n vertices. The

Let us now consider the group of all symmetries (both proper and improper rotations) of the regular n-gon. We call this group the dihedral group and denote it by Dn.

Example 3.17. Show that the dihedral group, Dn, is of order 2n and is not cyclic.

Solution. Label the vertices 1 to n in a counterclockwise direction around the n-gon. Let g be a counterclockwise rotation through 2π/n, and let h be the improper rotation of the n-gon about an axis through the center and vertex 1, as indicated in Figure 3.5. The element g generates the group Cn, which is a cyclic subgroup of Dn. The element h has order 2 and generates a subgroup {e, h}.

Any symmetry will fix the origin and is determined by the image of two adjacent vertices, say 1 and 2. The vertex 1 can be taken to any of the n vertices, and then 2 must be taken to one of the two vertices adjacent to the image of 1.

Dn = {e, g, g2, . . . , gn−1, h, gh, g2h, . . . , gn−1h}.

Note that if n 3, then gh = hg; thus Dn is a noncommutative group. Therefore, this group cannot be cyclic.

D2 can be defined as the symmetries of the figure in Figure 3.7. Hence D2 = {e, g, h, gh}, and each nonidentity element has order 2.

Note that the order of each of the elements h, gh, g2h, and g3h in D4 is 2. In general, the element gr h in Dn is a reflection in the line through the center

2

Figure 3.7. Symmetries of a 2-gon.