§2. Контрольные вопросы и задания

1. Дайте определение и приведите примеры групп.

2. Чем отличаются аддитивные и мультипликативные группы?

3. Является ли абелевой группой группа поворотов правильного треугольника?

4. Имеет ли группа перестановок трех элементов, абелевы подгруппы?

5. Дайте определение и приведите пример изоморфных групп.

6. Могут ли смежные классы одной подгруппы иметь непустое пересечение, но не совпадать?

7. Возведите перестановку в степень .

8. Перечислите основные группы линейных преобразований.

§3. Примеры решения задач

Задача 1. Образует ли множество ℤ₅ целых чисел, делящихся на пять без остатка, подгруппу группы целых чисел ℤ по сложению? А по умножению?

Решение. а) Проверим, является ли групповая операция сложения корректной в ℤ₅. Для этого рассмотрим ℤ₅. Тогда ℤ такие, что и . Рассматривая, заключаем чтоделится на 5 и, следовательно, ℤ₅. Операция сложения корректна в ℤ₅.

б) Принадлежит ли нейтральный элемент группы ℤ множеству ℤ₅? Поскольку элементом, нейтральным по сложению в ℤ, является число 0 и 0 делится на 5, делаем вывод о том, что ℤ₅.

в) Выберем произвольное число ℤ₅, т. е. ℤ. Очевидно, что элементом, противоположным к элементу , является элемент т. е. . Значит, каждый элементℤ₅ имеет противоположный, принадлежащий ℤ₅.

Из свойств а), б), в) следует, что ℤ₅ образует аддитивную подгруппу группы ℤ по сложению.

г) Для той же задачи с групповой операцией – операцией умножения вопрос о подгруппе ℤ₅ не возникает, ибо множество ℤ не является мультипликативной группой (элемент 0 обратного элемента не имеет).

Задача 2. Является ли подгруппа по сложению ℤ₅ нормальным делителем ℤ? Построить левые и правые смежные классы ℤ₅ в ℤ.

Решение. Ответ на вопрос задачи очень прост: в силу коммутативности операции сложения в группе левые и правые смежные классы совпадают и, следовательно, подгруппа ℤ₅ является нормальным делителем группы ℤ. А с построением смежных классов дело обстоит не так тривиально.

Подгруппа ℤ₅ состоит из элементов вида ℤ:

ℤ₅.

Построим правые смежные классы группы ℤ по подгруппе ℤ₅. Для построения смежного класса ℤ₅, где ℤ, надо ко всем элементам подгруппы ℤ₅ прибавить . Тогда:

ℤℤ₅,

ℤ1^.ℤ₅ ,

ℤ2^.ℤ₅ ,

ℤ3^.ℤ₅ ,

ℤ4^.ℤ₅ .

Таким образом, смежные классы ℤ,ℤ,ℤ,ℤ – это множества целых чисел, которые при делении на 5 дают положительный остаток 1, 2, 3 или 4 соответственно. Теперь заметим, что:

ℤ5^.ℤ₅ ℤℤ₅.

Следовательно, ℤ₅ ℤ=nℤ₅=ℤ₅. Что, впрочем, ясно не только из непосредственного счета, но и из свойств смежных классов. Далее укажем, что:

ℤ ℤ=ℤ=ℤ,

ℤ ℤ=ℤ=ℤ,

ℤ ℤ=ℤ=ℤ,

ℤ ℤ=ℤ=ℤ.

Итак, обнаружено что различных смежных классов группы ℤ по подгруппе ℤ₅ всего пять: ℤ=ℤ₅, ℤ, ℤ, ℤ, ℤ. При этом эти смежные классы не имеют общих элементов, что также подтверждается свойствами смежных классов.

Как отмечалось, в силу коммутативности групповой операции левые смежные классы ℤ₅совпадают с соответствующими правыми смежными классамиℤ₅, и, следовательно, подгруппа ℤ₅ является нормальным делителем группы ℤ.

Задача 3. Построить фактор-группу для аддитивной группы ℤ по нормальному делителю ℤ₅.

Решение. Рассмотрим множество смежных классов группы ℤ по подгруппе ℤ₅.

ℤ, ℤ, ℤ, ℤ, ℤ .

Введем на множестве групповую операцию, определяемую таблицей Кэли:

⊙	ℤ	ℤ	ℤ	ℤ	ℤ
ℤ	ℤ	ℤ	ℤ	ℤ	ℤ
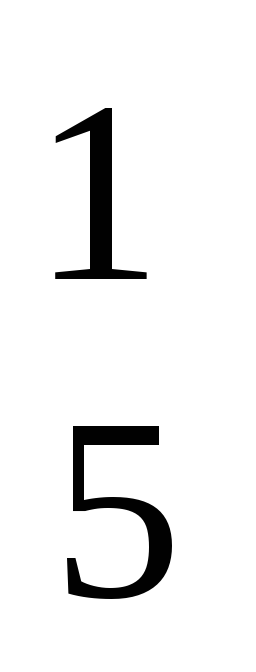
ℤ	ℤ	ℤ	ℤ	ℤ	ℤ
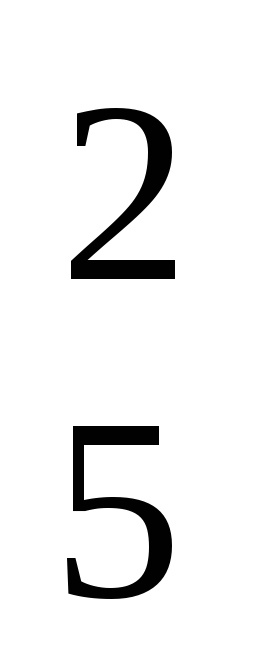
ℤ	ℤ	ℤ	ℤ	ℤ	ℤ
ℤ	ℤ	ℤ	ℤ	ℤ	ℤ
ℤ	ℤ	ℤ	ℤ	ℤ	ℤ

Приведенная таблица Кэли построена следующим образом: чтобы найти результат операции ℤ⊙ℤ следует найти суммуи положительный остатокот деления этой суммы на 5. Тогдаℤ⊙ℤ=ℤ.

При этом элемент ℤ=ℤ является элементом нейтральным по введенной операции, а элементы ℤ и ℤ, где – взаимно обратными.

Множество с так введенной групповой операцией образует группу (конечную и абелеву). Это и есть фактор-группа группыℤ по подгруппе ℤ.

Задача 4. Доказать, что группа комплексных чисел по сложению и группа параллельных переносов по умножению изоморфны.

Решение. Множество комплексных чисел ℂ по сложению образует абелеву группу.

Пусть – оператор параллельного переноса на вектор. Операция умножения параллельных переносов вводится как последовательное применение операторов переноса:⊙. Множество всех операторов параллельного переноса со стандартно введенной операцией умножения операторов также является абелевой группой.

Взаимно однозначное соответствие между элементами ℂ и установим следующим образом:ℂ . При таком отображении нейтральному элементу одной группы соответствует нейтральный элемент другой группы:

_ℂ.

Кроме того, если и, то:

1. с одной стороны – ⊙;

2. с другой стороны – .

Эти соотношения показывают, что образ суммы совпадает с произведением образов. Это и есть изоморфизм аддитивной группы ℂ и мультипликативной группы .

Задача 5. Найти с точностью до изоморфизма фактор-группу , если– группа ненулевых комплексных чисел по умножению,– группа комплексных чисел по модулю равных единице, по умножению.

Решение. Прежде всего, отметим, что есть подгруппа группыи, кроме того, в силу коммутативности групповой операции, является нормальным делителем группы. Для того чтобы построить фактор-группунеобходимо, прежде всего, найти смежные классы группыпо подгруппе.

Геометрическим местом точек на плоскости, которые соответствуют комплексным числам с модулем равным единице (подгруппа ), есть окружность единичного радиуса с центром в начале координат. И еще вспомним, что при умножении комплексных чисел аргументы комплексных чисел суммируются, а модули – перемножаются. Тогда при построении смежного классавсе элементыумножатся наи, следовательно:

а) произойдет поворот окружности вокруг начала координат на угол (окружность при этом повороте перейдет в ту же окружность) и

б) умножение ее радиуса на величину .

В результате смежным классом будет множество комплексных чисел, лежащих на окружности радиусас центром в начале координат.

Таким образом, множество смежных классов группы по подгруппеесть множество концентрических окружностей с центром в начале координат и ненулевого радиуса. Обозначим смежные классы:, где– радиус соответствующей окружности.

Групповую операцию определим следующим образом:⊙.

Нейтральным элементом по этой операции является сама подгруппа , а элементыиявляютсявзаимно обратными по введенной операции.

Множество всех смежных классов ℝ⁺) с так введенной операцией и есть фактор-группа .

Если каждому смежному классу ℝ⁺) поставить в соответствие вещественное положительное число ℝ⁺,а групповой операции в – операцию умножения вℝ⁺, то нетрудно убедиться (как в предыдущей задаче) в том, что факторгруппа изоморфна мультипликативной группеℝ⁺.

Задача 6. Перестановку разложить в произведение независимых циклов.

Решение. а) При последовательном применении данной перестановки элемент 1 переходит в 5, а затем элемент 5 переходит в 1 . Следовательно, после двукратного применения элементы 1 и 5 займут исходные места. Это явление носит название независимого цикла длины два в заданной перестановке и обозначается (1, 5).

б) В исходной перестановке нетрудно заметить еще два независимых цикла. Один – длины три (3, 9, 7), а другой – длины четыре (2, 8, 6, 4).

в) Полученные результаты можно записать следующим образом:

.

Такая запись называется разложением перестановки в произведение независимых циклов.

г) Отметим одно полезное следствие из полученного результата. Число 12 является наименьшим общим кратным длин циклов 2, 3 и 4, поэтому:

= .

Возведение перестановки в любую степень, кратную 12, не изменяет перестановку. Этот факт упрощает возведение перестановки в произвольную степень.