Все_лекции_Горбенко

Зазначену перевірку можна не виконувати, якщо використані в конкретній реалізації способи обчислення й зберігання базової точки гарантують виконання умов 1–4.

Порядок обчислення ключів ЦП

Розглянемо порядок обчислення асиметричної пари ключів (d, Q), тобто особистого d і відкритого Q ключів цифрового підпису.

Обчислення особистого ключа цифрового підпису

Особистий ключ d цифрового підпису повинен генеруватись (обчислюватись) таким чином:

1)обчислюється випадкове ціле число d згідно з п. 6.3 стандарту;

2)перевіряється умова d 0 ; якщо вона виконується, то d обирають як особистий ключ цифрового підпису, інакше переходимо до кроку 6.

Необхідно відзначити, що недопустимим є використання особистого ключа d 1 та d n 1, оскільки в цьому випадку відкритий ключ Q співпаде з базовою точкою G, що повністю компрометує такий особистий ключ.

Умови обчислення й зберігання особистого ключа цифрового підпису мають унеможливлювати несанкціонований доступ до нього або його частини, а також до проміжних даних, які використовувалися в процесі обчислення особистого ключа. Окрім того, умови зберігання та використання особистого ключа повинні унеможливлювати його модифікацію, знищення або підміну. Цього можна досягти, використовуючи апаратні засоби зберігання та використання особистих ключів.

Обчислення відкритого ключа цифрового підпису

Відкритий ключ цифрового підпису обчислюється у вигляді точки з використанням скалярного множення вигляду Q = – dP, де Р – як і раніше, базова точка. Використання від’ємного знаку пов’язане з прискоренням за таких умов обчислення цифрового підпису.

Відносно відкритого ключа мають бути забезпечені послуги його цілісності, справжності й доступності, у цьому забезпечується практична захищеність від модифікації, підміни та викривлення відкритого ключа цифрового підпису. Основним способом забезпечення таких властивостей є використання послуг третьої довірчої сторони, для національних систем – це використання послуг акредитованих центрів сертифікації ключів, тобто виготовлення й обслуговування сертифікатів відкритих ключів.

Перевірка правильності ключів ЦП

Необхідний рівень криптографічної стійкості ЦП від різних загроз і атак може бути забезпечений за умови забезпечення цілісності, справжності й доступності до асиметричної пари ключів (d, Q). Указане забезпечується постійною перевіркою правильності відкритого й особистого ключів цифрового підпису.

Перевірка правильності відкритого ключа ЦП

Відкритий ключ Q цифрового підпису, як правило, має використовуватись у вигляді сертифіката відкритого ключа і задовольняти таким умовам:

1)координати точки еліптичної кривої, що визначають відкритий ключ цифрового підпису, належать основному полю, тобто є двійковими рядками довжини m;

2)відкритий ключ задовольняє умові Q O (він також має задовольняти умові Q P , тобто d = 1);

3)відкритий ключ Q (xQ , yQ ) задовольняє рівнянню використовуваної еліптичної

кривої;

4)порядок точки n такий, що nQ = 0.

Якщо умови 1–4 виконані, то відкритий ключ цифрового підпису правильний.

Таку перевірку на практиці можна не виконувати, якщо використані в конкретній реалізації алгоритму цифрового підписування засоби зберігання й використання відкритого ключа цифрового підпису унеможливлюють його підміну, модифікацію чи знищення.

Перевірка правильності особистого ключа

Перевірка правильності особистого ключа виконується тільки власником особистого ключа. Вона має виконуватися таким чином:

1.Обчислюється точка еліптичної кривої Q dP, причому Р – базова точка еліптичної кривої, а d – особистий ключ цифрового підпису.

2.Якщо Q Q, де Q – відкритий ключ цифрового підпису, то особистий ключ відповідає відкритому ключу цифрового підпису і є правильним.

Зазначену перевірку можна не виконувати, якщо використані в конкретній реалізації алгоритму ЦП засоби зберігання й використання особистого ключа практично виключають його підміну, модифікацію чи знищення.

Порядок обчислення цифрового передпідпису

Оскільки в стандарті особистий (таємний) ключ сеансу не залежить від повідомлення (інформації), що підписується, то попередньо він може бути обчислений і зберігатися в захищеному вигляді. У національному стандарті визначено такий механізм обчислення цифрового передпідпису.

Вхідними даними для формування цифрового передпідпису є загальні параметри.

Результатом виконання алгоритму є цифровий передпідпис Fe, що відповідає

таємному випадковому параметру е, де е – ціле число, 0 e n, Fe GF(2m ), а n – порядок базової точки. (Зазвичай для інших ЦП особисте значення е позначалося літерою k. Але, зважаючи на позначення в стандарті, ми використовуємо символ е).

Алгоритм обчислення цифрового передпідпису такий:

1.Обчислюється випадкове ціле число е згідно з п.6.3 стандарту.

2.Обчислюється точка еліптичної кривої R = e P = (xR , yR ).

3.Якщо координата xR 0 , то перейти до кроку 1, інакше Fe xR і необхідно перейти до кроку 4.

4.Результат виконання алгоритму – цифровий передпідпис Fe і таємний випадковий параметр е.

Необхідно зауважити, що умови обчислення, зберігання й використання таємного параметра е мають унеможливлювати несанкціонований доступ до нього, його частин, а також до проміжних даних, які використовувалися в процесі обчислення цифрового передпідпису.

Припускається попереднє обчислення необхідного числа цифрових передпідписів, але за умови унеможливлення його модифікації чи підміни, а також обов’язкового знищення разом з відповідним таємним параметром е.

Порядок обчислення ЦП

Обчислення ЦП має виконуватися в такому порядку. Задані та є доступними такі вхідні дані:

-загальні параметри цифрового підпису;

-особистий ключ цифрового підпису d;

-повідомлення Т довжини LT 0 ;

-функція гешування H згідно з п.6.2 стандарту;

- довжина цифрового підпису LD , що вибирається для групи користувачів, виходячи з умов конкретної реалізації алгоритму цифрового підпису з урахуванням умов кроку 3 наведеного нижче алгоритму.

Результат виконання алгоритму: повідомлення Т і цифровий підпис D, що дають

змогу утворити підписане повідомлення у вигляді(iH ,T, D) .

Алгоритм цифрового підписування

1.Перевіряється правильність загальних параметрів цифрового підпису згідно з п. 8.1–8.3 стандарту. Якщо загальні параметри цифрового підпису обчислено неправильно, то обчислення цифрового підпису припиняється.

2.Перевіряється правильність особистого ключа цифрового підпису згідно з п. 10.2 стандарту. Якщо особистий ключ неправильний, то обчислення цифрового підпису припиняють.

3.Перевіряється виконання умов: LD – число, кратне 16; LD 2L(n) . Якщо хоча б одна із цих умов не виконується, то обчислення цифрового підпису припиняється.

4.Якщо використовується ідентифікатор геш-функції iH, то перевіряється, чи діє цей ідентифікатор у відповідній групі користувачів. Якщо ні, то обчислення цифрового підпису припиняється.

5.Якщо нормативні документи, що визначають порядок обчислення функції гешування, накладають обмеження на довжину повідомлення LT , то перевіряють виконання цих обмежень. Якщо ці обмеження не виконані, або повідомлення відсутнє, або LT 0 , то обчислення цифрового підпису припиняється.

6.Для повідомлення Т обчисляється геш-значення h = H(T).

7.Результат обчислення функції гешування H(T) перетворюють на елемент основного поля h згідно з п. 6.9 стандарту. Якщо h = 0, то приймають h = 1.

8.Якщо вже існує набір цифрових передпідписів, обчислених заздалегідь, то береться будь-який із них разом з відповідним таємним параметром. Інакше цифровий передпідпис обчислюється в спосіб, указаний вище в п. 2.6.6.

9.Обчислюється елемент основного поля y hFe .

10.Елемент основного поля y перетворюють на ціле число r згідно з п.6.8 стандарту.

11.Якщо r = 0, то перейти до кроку 8; інакше перейти до кроку 12.

12.Обчислюється значення підпису у вигляді цілого числа s (e dr)mod n . 13.Якщо s = 0, то перейти до кроку8; інакше перейти до кроку 14.

14. Пару цілих чисел (r,s) перетворюють на цифровий підпис D довжиною LD згідно з п.6.10 стандарту.

Результат виконання алгоритму – підписане повідомлення (iH,T,D) .

Порядок перевіряння ЦП

Перевіряння ЦП виконується в такому порядку. Заданими та доступними є такі вхідні дані:

-загальні параметри цифрового підпису;

-відкритий ключ цифрового підпису підписувача Q;

-підписане повідомлення (iH ,T,D) довжиною L L(iH ) LT LD ;

-функція гешування H згідно з п.6.2 стандарту.

Результатом виконання алгоритму є повідомлення «підпис дійсний» або «підпис не дійсний».

Алгоритм перевіряння цифрового підпису:

1.Якщо використовується ідентифікатор геш-функції iH, то перевіряється, чи діє цей ідентифікатор у відповідній групі користувачів. Якщо ні, то видається повідомлення «підпис не дійсний» і припиняється перевіряння ЦП.

2.Виходячи з iH (або за умовчуванням), визначають LH .

3. Перевіряється виконання умов, що LD – число, кратне 16, та LD 2L(n). Якщо хоча б одна з цих умов не виконується, то видається повідомлення «підпис не дійсний» і перевірку припиняють.

4.Перевіряють правильність обчислення загальних параметрів цифрового підпису згідно з пп. 8.1–8.3 стандарту. Якщо загальні параметри цифрового підпису обчислено неправильно, то видається повідомлення «підпис не дійсний» і перевірку припиняють.

5.Згідно з п.10.1 стандарту ДСТУ 4145 - 2002 перевіряється правильність відкритого ключа ЦП. Якщо відкритий ключ обчислено неправильно, то видають повідомлення «підпис не дійсний» і перевірку припиняють.

6.Обчислюється LT L LD L(iH ) . У випадку відсутності тексту, або при LT 0 видається повідомлення «підпис недійсний» і перевірку припиняють. Якщо нормативні документи, які встановлюють обчислення функції гешування, накладають обмеження на

довжину повідомлення LT , то перевіряють виконання цих умов. Якщо ці умови не виконані, то видають повідомлення «підпис недійсний» і перевірку підпису припиняють.

7.Для повідомлення Т обчислюється геш-значення h = Н(Т).

Геш-значення Н(Т) перетворюється на елемент основного поля h згідно з п.6.9 стандарту. Якщо h = 0, то приймається h = 1.

8.Згідно з п.6.11 стандарту цифровий підпис D перетворюється на пару цілих чисел (r,s). Якщо умова 0 < r < n не виконана, то видається повідомлення «підпис не дійсний»

іперевірка припиняється.

9.Якщо умова 0 < s < n не виконана, то видається повідомлення «підпис не дійсний» і перевірка припиняється.

10.Обчислюється точка еліптичної кривої R sP rQ, R (xR , yR ) .

16.Обчислюється елемент основного поля y hx R .

є правильними. Для цього зробимо такі перетворення. Помножимо ліві та праві частини (6.62) на базову точку P. У результаті маємо:

s P = e P + r Q.

За умови, що R = e P = (x R , yR ) маємо, що

R = s P – r Q.

Зурахуванням того, що Q = – d P отримаємо (6.62).

3.5Аналіз алгоритмів направленого шифрування ISO/IEC 18033-2

ACE-KEM

Криптосистема ACE-KEM заснована на роботі Cramer і Shoup [41] і навмисно призначена бути безпечною не вимагаючи евристичної випадкової моделі оракула. Криптосистема була представлена на конкурс NESSIE IBM. Схема складається з наступних алгоритмів. Закінчені технічні вимоги даються в [42].

1 Проект

Генерація ключів. ACE-KEM описана в абстрактній групі і може бути реалізована або як схема на еліптичній кривій, або як схема, що працює в мультиплікативній групі цілих чисел для деякого модуля. Групу представляється як адитивна, де елементи групи позначені заголовними буквами (як у групі точок еліптичної кривої). Припускається, що група є циклічною, згенерованою деяким елементом P порядку p, і що p має довжину, рівну параметру безпеки . Алгоритм генерації ключів є імовірнісним алгоритмом, що бере параметри групи (P, p, ) як вхідні значення. Алгоритм виконується за таким способом.

Алгоритм інкапсуляції. Алгоритм інкапсуляції є імовірнісним алгоритмом, для якого вхідними даними є відкритий ключ pk. Алгоритм використовує загальновідому й предпогоджену ґеш-функцію Hash( ) й функцію вироблення ключів KDF( ). Алгоритм виконується за таким способом.

1.Генерується випадкове ціле число r 0,..., p 1 .

2.Покладається (Установлюється) C1 : rP.

3.Установлюється C2 : rW .

4.Установлюється Q : rZ

5.Установлюється Hash(C1 C2 ).

6.Установлюється C3 : rX rY .

7.Установлюється C: (C1, C2, C3).

8.Установлюється K: KDF(C1 Q).

2.Виводиться інкапсульована пара ключів (K,C).

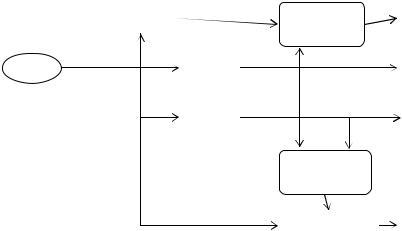
Алгоритм інкапсуляції ACE-KEM представлений на рис. 1.

Рисунок 1 – Алгоритм інкапсуляції ACE-KEM.

Алгоритм декапсуляції. Алгоритм декапсуляії є детермінованим алгоритмом, вхідними даними для якого є інкапсульований ключ C і секретний ключ sk. Алгоритм також використовує предпогоджену ґеш-функцію Hash( ) й функцію вироблення ключів

KDF( ). Алгоритм виконується за таким способом.

1.Представити інкапсульований ключ C як (C1, C2, C3).

2.Установити : Hash(C1 C2 ).

3 Установити t : x y .

4. Перевірити, що C2 wC1. У противному випадку вивести, що зашифрований текст невірний (Invalid Ciphertext) і закінчити виконання алгоритму.

5.Перевірити, що C3 tC1. У противному випадку вивести, що зашифрований текст невірний (Invalid Ciphertext) і закінчити виконання алгоритму.

6.Установити Q: zC1.

7.Установити K: KDF(C1 Q) .

8.Вивести K.

Аналіз безпеки

Більш докладний аналіз безпеки ACE-KEM наведений в [48, 44].

Основна перевага ACE-KEM полягає в тому, що безпека схеми може бути доведена без використання евристичної випадкової моделі оракула (див. Пункт 1.4). Це поєднується приємно з доказом безпеки для універсальної гібридної конструкції, обговореної в пункті 2.5, щоб сформувати гібридну схему, що є доказово безпечною без потреби у випадкових оракулах.

Доведення безпеки для ACE-KEM [41] приводить проблему злому ACE-KEM в INDCCA2 змісті до проблеми вирішення розв’язуваній Діффі-Хеллмана проблеми (decisional Diffie-Hellman problem) в групі, що згенерована P. Оскільки ми не моделюємо ґеш-функцію, або функцію вироблення ключів як випадкових оракулів, то ми повинні формально визначити умови їхньої безпеки.

Визначення 16. Геш-функція Hash( )є стійкою до 2-го прообразу, якщо, знаючи значення x, неможливо знайти значення y xтаке, що Hash(x) Hash(y). Ми визначаємо

(t, ) криптоаналітика для ґеш-функції, як імовірнісну машину Тюрінга, що за час не більше ніж t при даному х згенерованому випадковим образом, знаходить другий прообраз із імовірністю не менш ніж .

Визначення 17.Функція вироблення ключів KDF( ) є нерозрізненою, якщо при даному

криптоаналітика для функції вироблення ключів, як імовірнісну машину Тюрінга, що за час не більше t вирішує вище згадану проблему з імовірністю не менш1/2 .

Якщо для ACE-KEM у змісті IND-CCA2 існує (t, , q) криптоаналітик, то існує (t1, 1) вирішувач для розв’язуваній Діффі-Хеллмана проблеми (decisional Diffie-Hellman problem) в

Поки приведення до розв’язуваній Діффі-Хеллмана проблеми (DDH проблеми) єважким, припущення, що DDH проблема є важкою є досить сильним. Для кращого порівняння з існуючими схемами також було показано, що ACE-KEM безпечно не менша чим ECIES-KEM (див. Пункт 2.3). Формально, якщо для ACE-KEM існує (t, , q) криптоаналітик, то існує (t, , q) криптоаналітик для ECIES-KEM. Це служить показанням, що, у випадковій оракульній моделі, безпека ACE-KEM в IND-CCA2 змісті пов’язана з проблемою прорива Діффі-Хеллмана проблеми (gap Diffie-Hellman problem) в групі, що згенерована P.

Відносини між ACE-KEM й ECIES-KEM також означають, що в моделі IND-CPA з допомогою випадкової моделі оракула, захист ACE-KEM може бути зведений до

обчислювальній проблеми Diffie-Hellman (CDH) у групі P .1 Формально, якщо для ACEKEM існує (t, ) крипто аналітик, то там існує алгоритм, що за час t виводить список елементів L, що містить рішення CDH проблеми з імовірністю не менше

де криптоаналітик робить якнайбільше qk запитів випадкового оракула, який моделює функцію вироблення ключів. Звичайно, ми можемо тепер використати методи пункту 2.2.2, щоб створити (t , ) вирішальний пристрій для CDH проблеми з

Q, p, q прості числа. Ця схема має недолік роботи в певній мультиплікативній групі (і також буде ймовірно мати більше довгі ключі, ніж версія еліптичної кривої), але має ймовірність більш сильного доказу безпеки. Схема Lucks безпечна в стандартній моделі, що забезпечує проблему розкладання на множники й DDH проблемі в групі модуля квадратичних лишків n. Ця схема є гірша, ніж ACE-KEM, оскільки ACE-KEM не вимагає щоб проблема розкладання на множники була важкою. Однак, у випадковій оракульній моделі, схема Lucks приводить до рішення CDH проблеми дуже ефективним способом. Це є істотним уточненням по ACEKEM у теоретичній безпеці.

Поряд з більшістю інших асиметричних схем шифрування, ACE-KEM вразлива до атаки дефектів (fault attack), що повертає секретний ключ [37]. Схема також уразлива силовому аналізу в процесі скалярного множення дефектів еліптичної кривої. Це звичайна проблема для схем, заснованих на еліптичних кривих.

1 В моделі атаки IND-CCA2, і використаній моделі випадкового оракула, безпека ACE-KEM може бути безпосередньо зведена до CDH проблеми в групі, що згенерована P [62]. Однак це приведення зовсім не однозначно.

2 ECIES

ECIES гібридна схема шифрування, представлена на NESSIE Certicom Corp. Вона складається з нижче описаних алгоритмів. Закінчені технічні вимоги можуть бути знайдені в

[50].

2.2.1 Проект

Генерація ключів. Тому що ECIES – криптосистема на еліптичних кривих, необхідно згенерувати безпечну еліптичну криву E і точку P E порядку p. Припустимо, що значення p дорівнює параметру безпеки . Алгоритм генерації ключів для ECIES є імовірнісним алгоритмом, для якого вхідними даними є (E,P, p, ) . Алгоритм виконується за таким

способом (позначимо точку на нескінченності еліптичної кривої).

1.випадковим образом генерується ціле число s {1,..., p 1}.

2.Установлюється W: sP.

Алгоритм шифрування. Алгоритм шифрування імовірнісний алгоритм, для якого вхідними даними є повідомлення m й відкритий ключ pk . Схема також припускає

наявність публічних (відкритих) предузгоджених функцій, які є доступними всім сторонам. Вони включають функцію вироблення ключів KDF(), алгоритм автентифікації

повідомлень MAC , і симетричну схему шифрування (Sym.Encrypt,Sym.Decrypt).

Алгоритм виконується за таким способом (позначимо нескінченно вилучену точку еліптичної кривої, яка є тотожнім елементом).

1. Генерується випадкове ціле число r {1,..., p 1}.

2.Установлюється C1: rP

3.Установлюється Q : rW .

4.Перевіряється, що Q . Якщо це так, то виводиться Invalid Encryption і виконання

алгоритму зупиняється.

5.Установлюється x, як x-координатаQ .

6.Установлюється K: KDF(x).

7.Розглядається K як EK і МК, де EK ключ для симетричної схеми шифрування і МК підходящий розмір ключа для схеми автентифікації повідомлення. 2

8.Зашифровується повідомлення m, використовуючи симетричну схему шифрування на ключі EK, тобто C2: Sym.Encrypt(m, EK).

2. Виводиться криптограма C: (C1, C2, C3).

Алгоритм розшифрування. Алгоритм розшифрування детермінований алгоритм, вхідними даними якого є криптограма C і секретний ключ sk. Алгоритм також використовує ту ж саму предузгоджену функцію вироблення ключів KDF( ), алгоритм автентифікації

повідомлення MAC(,) й симетричну схему шифрування (Sym.Encrypt, Sym.Decrypt) як в

алгоритмі шифрування. Алгоритм виконується за таким способом.

2якщо довжини EK и МК не предвизначені, то застосовується атака Shoup [42, 15.6.4].

1.Представити C як (C1 ,C2 ,C3 ).

2.Установити Q : sC1.

3.Перевірити що Q O. Якщо так, вивести Invalid Ciphertext і зупинити виконання

алгоритму.

4.Установити x, як x-координату Q.

5.Установити K : KDF (x).

6.Представити K як EK і МК, де EK підходящого розміру ключ для симетричної схеми шифрування і МК підходящого розміру ключ для схеми автентифікації повідомлення.

7.Перевірити що C3 вірний код автентифікації повідомлення для C2 на ключі MK,

тобто C3 MAC(C2, MK). У противному випадку вивести Invalid Ciphertext і зупинити виконання алгоритму.

8. Розшифрувати зашифрований текст C2 , використовуючи симетричну схему шифрування на ключі EK, тобто m: Sym.Decrypt(C2, EK) .

2. Вивести m.

Аналіз безпеки

Нижче приводяться підсумки аналізу безпеки ECIES; для більш докладної інформації див. [51].

У першу чергу варто звернути увагу на те, що алгоритм ECIES не безпечний у моделі IND-CCA2. Якщо криптоаналітик одержує зашифрований текст (C1, C2, C3), то він може

піддати зашифруванню текст ( C1,C2,C3) розшифруючим оракулом (забезпечивши, що

C1 C1 умову, яка відбувається з дуже великою ймовірністю) і оракул поверне

правильне повідомлення m. Тому, якщо ми збираємося знайти будь який значимий результат про безпеку ECIES у цій моделі, то ми повинні формально заперечувати здатність криптоаналітика робити ці запити. Shoup [42] назвав цю властивість полегшеною пристосовністю (benign malleability).

Доказ захисту для ECIES наведений в [52]. Цей документ описує безпеку схеми DHAES, подібну до схеми ECIES, але визначену на абстрактній циклічній групі порядку p, скоріше ніж специфічно у групі еліптичної кривої. DHAES відрізняється від ECIES генерацією симетричного ключа K який, в DHAES одержують із повного подання Q і з C1 .

Доказ безпеки показує, що, якщо передбачена симетрична схема шифрування й MAC є безпечними в деякому змісті, то проблема злому схеми приводиться до проблеми розрізнення вихідних дані функції вироблення ключів від випадкового рядка того ж самого розміру. Доказ захисту для ECIES в універсальній моделі групи (див. Пункт 1.5) запропонований в [53].

ECIES власне кажучи приклад ECIES-KEM (див. Пункт 2.3), яка використовується зі специфічним механізмом інкапсуляції даних (відомим як DEM-1 [42]). Мі думаємо, що ECIES-KEM буде більше гнучким, чим ECIES, без застосування обчислень або втрати безпеки.

3 ECIES-KEM

ECIES-KEM, власне кажучи, асиметрична основа ECIES, описаного в структурі KEMDEM. Хоча ECIES-KEM ніколи не був формально представлений проекту NESSIE, ECIESKEM розглядався NESSIE, оскільки де факто це стандарт для криптосистеми KEM-DEM і тому що ECIES-KEM була запропонована для стандартизації в ISO/IEC 18033-2 [42]. ECIESKEM складається з нижче описаних алгоритмів. Закінчені технічні вимоги можуть бути знайдені в [42].

2.2.1 Проект

Генерація ключів. ECIES-KEM, подібно ECIES, є схемою на еліптичній кривій. Це означає, що перш, ніж схема може бути реалізована, повинна бути згенерирована безпечна еліптична крива E, і повинна бути обрана базова точка P E порядку p. Ми припускаємо, що значення p дорівнює параметру захисту .

Алгоритм генерації ключів є імовірнісним алгоритмом, для якого вхідні дані це параметри еліптичної кривої (E,P, p, ), і який виконується за таким способом.

1.Випадковим образом згенерувати ціле число s 1,..., p 1 .

2.Установити W : sP.

Алгоритм інкапсуляції. Алгоритм інкапсуляції є імовірнісним алгоритмом, вхідними даними для якого є відкритий ключ. Алгоритм використовує суспільну предузгоджену функцію вироблення ключів KDF( ), доступну всім сторонам, які бажають використати схему. Алгоритм інкапсуляції виконується за таким способом.

1.Генерується випадкове ціле число r 1,..., p 1 .

2.Встановлюється C : rP

3.Встановлюється x, як x-координату rW .

4.Встановлюється K: KDF(Cx).

5.Виводиться інкапсульована пара ключів (K,C).

Алгоритм декапсуляції. Алгоритм декапсулації є детермінованим алгоритмом, для якого вхідними даними є інкапсульований ключ C і секретний ключ sk. Алгоритм також використовує предузгоджену функцію вироблення ключів KDF( ), що була використана в процесі інкапсуляції. Алгоритм виконується за таким способом ( позначена нескінченно вилучена точка еліптичної кривої).

1.Q: sC .

2.Перевірити що Q O. Якщо так, вивести Invalid Ciphertext і зупинити виконання

алгоритму.

3.Установити x, як x-координату Q.

4.Установити K: KDF(Cx).

5.Вивести K.

Аналіз безпеки

Просто показати, що ECIES-KEM є IND-CCA2 безпечною у випадковій моделі оракула [45]. Безпека схеми може бути дуже ефективно приведена до проблеми Gap-DH у підгрупі

де q є числом запитів, які криптоаналітик представляє випадковому оракулу, що моделює функцію вироблення ключів, і Tє часом, необхідним для перевірки тріади Діффі-Хеллмана

тріади (тобто час, необхідний для оракула, щоб перевірити для тріади

ga,gb,gc ).