16. Общая характеристика методов.

Предположим, что в мерном пространстве переменныхзаданы случайная точкас функцией распределенияи некоторая область. Рассмотрим одномерную случайную величинуопределенную формулой

при (36)

Для расчета по этой формуле можно выбрать случайную точку в пространстве; еслито вычисляется; еслито точкаотбрасывается и выбирается новая. Таким образом, при расчете по формуле (36) из случайных точекс функцией распределенияотбирают точки, принадлежащие, и по ним вычисляют. Мы будем говорить, что формула (36) определяет метод отбора для моделирования.

Эффективностью метода отбора называют вероятность отбора или, более подробно, вероятность того, что точкабудет использована для расчета, а не будет отброшена. Очевидно, эффективность метода (36) равно вероятности (37)

Выбрав точекмы получим в среднем всегозначений.следовательно, на расчет каждого значениязатрачивается в среднем 1/э точек.ясно, что при малых э метод (36) становится практически неэффективным.

Если на реализацию каждой точки затрачиваютсяслучайных чиселгде, очевидно,то в среднем на одно значениезатрачиваетсяслучайных чисел. В вычислительной практике (при моделировании одновременных величин) чаще всего встречаются случайи.

16. Метод Неймана.

Рассмотрим случайную величину , определенную на конечном интервалес ограниченной плотностью(рис.30).

Рис.29. Рис.30.

Еслинезависимые случайные числа иСлучайная величина, определенная условием(39)

имеет плотность вероятностей, равную

Эффективность метода (39), равна вероятности попадания точи под кривуют.е.Последняя вероятность уже вычислялась в ходе доказательства теоремы. Значит,

эффективность метода Неймана будет наибольшей, если выбрать наименьшее возможное т.е. положитьВпрочем, это очевидно также из геометрических соображений.

16. Модифицированный метод Неймана.

17. Else //повтор снова

If () then

16. Метод Метрополиса

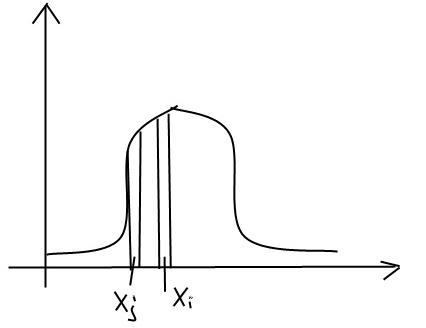
Эргодическая теорема: Данные просмотра 1 частицы и данные просмотра многих в фиксированый момент времени совпадают.

Алгоритм: 1.

2.

3. if W1 then

4. if W<1

If then

Else

16. Моделирование усеченных распределений.

Рассмотрим случайную величину , определенную а интервалес плотностью(так что).

Говорят, что случайная величина имеет усеченное распределение, если она определенна в интервалеи плотность ее порпорциональна.

Очевидно, см. рис. 29, где

Если мы умеем вычислить значение , то значенияможно находить методом отбора:

.(38) Эффективность такого метода равна

16. Выбор равномерно распределенных точек в сложных пространственных областях.

Пусть В – ограниченная область на плоскости х, у, «сложная» с точки зрения вычислительной практики: например, невыпуклая или несвязная или такая, что границы на отдельных участках трудно записать в явном виде. Выберем прямоугольник , содержащий область В (рис. 32). Координаты случайной точки

, равномерно распределенной в П, легко вычислить:

.

Для нахождения точек , равномерно распределенных в В, можно вычислять точки, равномерно распределенные в П, и отбирать среди них те, которые принадлежат В. В самом деле, для любой области

.

Так как равномерно распределена в П, то вероятность попаданияв любую область пропорциональна площади этой области:,. Следовательно,

или, что то же, плотность в области В.

Эффективность такого метода равна отношению площадей

Поэтому э будет наибольшей тогда, когда площадь П минимальна – результат очевидный геометрически. Ясно также, что в тех случаях, когда область В хорошо вписывается, например, в круг (рис. 33), лучше не пользоваться прямоугольником П, а отбирать точкииз числа точек, равномерно распределенных в С. Эффективность такого методабудет выше, ибо.