16. Моделирование случайных непрерывных величин.

Предположим, что случайная величина  определена в интервале а<х<b и имеет плотность р(x)>0 при а<х<b. Обозначим через F(x) функцию распределе­ния , которая при а < х < b равна

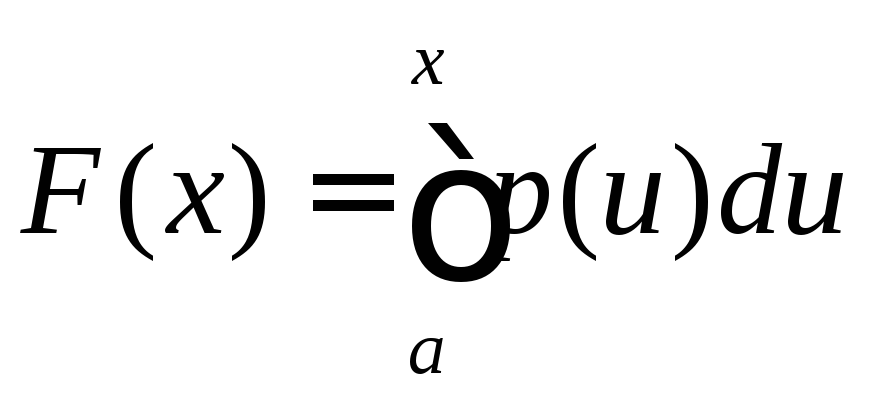
Случай a = –  и (или) b =  не исключается.

В тех случаях, когда уравнение F() =  (4) аналитически разрешимо относительно , получается явная формула  = G() для разыгрывания случайной величины , где G(y) – обратная функция по отношению к y = F(x). В других случаях можно уравнение (4) решать числен­но. Если объем накопителя позволяет, то удобно соста­вить таблицу функции G(y), 0<y<1, и по ней нахо­дить значения . Иногда удобно использовать таблицу функции F(x), а < x < b, и находить значения  обрат­ной интерполяцией.

П р и м е р. Экспоненциальная случайная величина  определена при x₀ < x <  с плотностью

p(x) = a e ^{– a ( x – x0 )} .

Так как 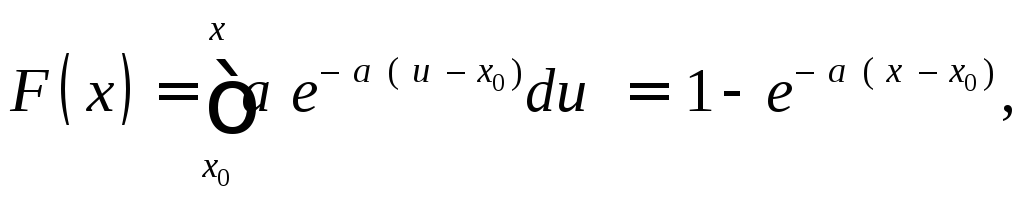то уравнение (4) принимает вид

1 – e ^{– a (  – x0 )} = .

Отсюда получаем явное выражение для расчета :  = x₀ – (1/а)1n(1– ). (5)

16. Моделирование многомерной случайной точки.

Моделирование n-мерной случайной точки с независимыми координатами. Если координаты n-мерной случайной величины Q=(ξ₁, ..., ξ_n) независимы, то функция распределения

F_Q(x₁, ..., x_n) = F₁(x₁)... F_n(x_n),

где F_i(x_i) – функция распределения величины ξ_i. Есте­ственно ожидать, что в этом случае можно моделиро­вать каждую величину ξ_i независимо:

F_i(ξ_i) = γ_i , i = 1,2, ...,n, (11)

где γ_i , ..., γ_n – независимые случайные числа.

Действительно, так как γ_i независимы, то и ξ_i опре­деленные формулами (11), независимы. Поэтому их совместная функция распределения равна произведению

_{n n}

Р{ξ₁ < x₁ ,... ,ξ_n <х_п} = П Р{ ξ_i < x_i} = П F_i(x_i) = F_Q(x₁, ..., x_n).

^{i = 1 i = 1}

16. Поправки к приближенным распределениям.

Предположим, что плотность р(х) случай­ной величины ξ аппроксимируется снизу достаточно про­стой линией у(х). Оче­видно, в качестве приближения к р(х) можно выбрать плотность

p₁(x) = y(x) / c, где

b

c₁ = ∫ y(x) dx, и находить приближенные значения ξ по плотности p₁(x).

a

Можно, однако, представить р(х) в форме суперпо­зиции двух плотностей

p₁(x) = y(x) / c₁ и p₂(x) = [p(x) – y(x)] / c₂,

и получить таким образом метод для точного моделирования ξ. Алгоритм расчета ξ по плотности р(х) может оказаться весьма сложным; но на времени счета это почти не скажется, ибо р₂(х) будет использоваться очень редко: Р{η = 2} = с₂ = 1 – c₁ << c₁.

Итак, метод суперпозиции дает возможность учесть «поправку» p₂(x), практически не увеличивая времени счета, а лишь ценою усложнения программы (впрочем, обычно это весьма нежелательно).

16. Разделение области моделирования случайной величины.

Этот прием иногда используют при моделировании случайной величины, плотность ко­торой резко различна в различных областях.

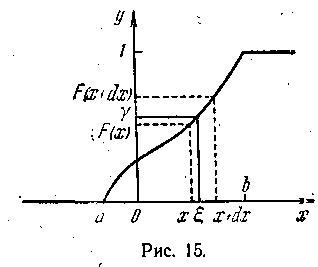
Пусть р(х)—плотность случайной величины ξ, определенной в интервале а < x < b. Разобьем этот интервал на сумму непересекаю­щихся интервалов ∆_k, так что (a, b) = ∆₁ + … +∆_m (рис. 27) и веро­ятности попадания ξ в ∆_k положительны: с_k = _∆k∫ p(x) dx > 0.

Введем в рассмотрение плотности

p(x) / c_k при x∆_k,

p_k(x) =

0 при x∆_k,.

Очевидно, c₁ + … +c_m = 1 и при всех х из (а; b)

p(x) = c₁p₁(x) + … + c_m p_m(x).

Для того чтобы найти значение ξ, можно сперва по числу γ₁ разыграть номер области η = k, а затем вычис­лить ξ из уравнения

, (21)

где a_k – левый конец ∆_k.

Легко проверить, что с точки зрения количества вычислений этот метод хуже, чем метод обратных функций.

можно решать следующим образом: сперва найдем номер k такой, что

k–1 k

∑ c_j ≤  < ∑c_j; (22)

j=1 j=1

тогда это уравнение превратится в уравнение

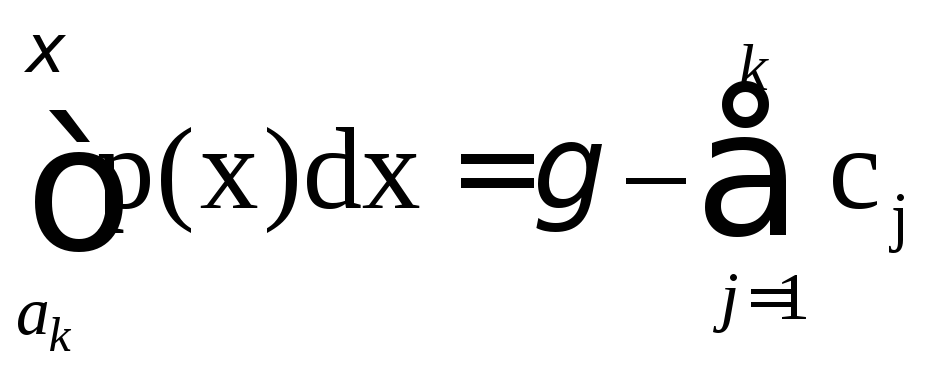(23)

решая которое и найдем ξ. Уравнение (23) проще, чем (21), и совпа­дает с уравнением модифицированного метода суперпозиции для рассматриваемой задачи.

Положение может резко измениться в пользу метода дробления области, если вместо (21) использовать для моделирования ξ с плотностью p_k(х), в ∆_k какой-нибудь другой способ. Правда, тогда на получение одного значения ξ будет затрачиваться больше двух случайных чисел.

Метод дробления области применим также для моделирования многомерных случайных величин [19].