Двойные и тройные интегралы

1.

Демидович. 39(06,08,13,16,18,19,24,27,30,31,

37,40,51,62. 57,67,71,74).

Вычислить интегралы:

3906..3908. .

3913. Найти среднее значение функции f (x ,y)=в квадрате.

Расставить пределы интегрирования в различном порядке:

3916.-треугольник с вершинами О(0,0);A(1,0);B(0,1).

19

3918.– трапеция с вершинами O(0,0);A(1,0);B(1,2);C(0,1).

3919. Определить пределы интегрирования по гдекруг

Изменить порядок интегрирования.

3924.. 3927.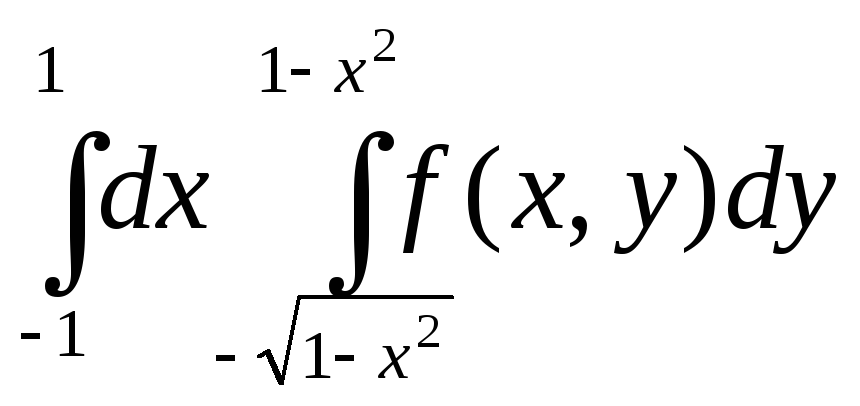.3930..3931..

Расставить пределы интегрирования в полярной системе координат.

3937.

3940.

Заменить двойные интегралы однократными, переходя к новой системе координат.

3951..3962..

Сделать замену переменных в двойных интегралах:

3957.(0 <a <b, 0 <u = x, v =

Вычислить:

3967..

3971.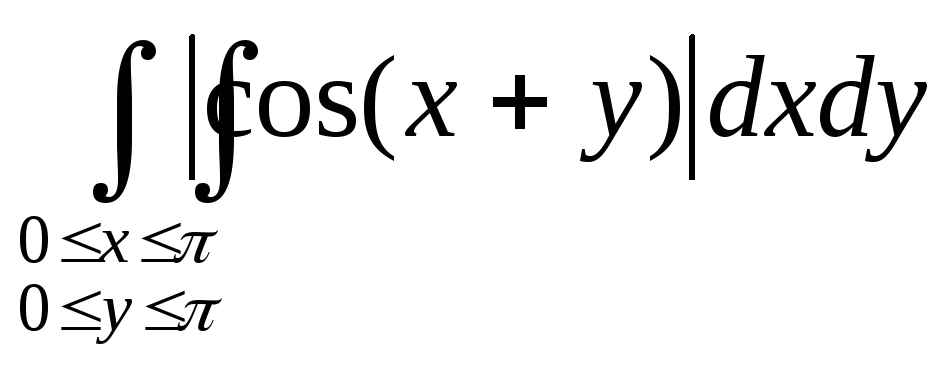.3974..

2.

Демидович 39(84,87,97), 40(07,09,18,21,36,

37,41,52,73)

Вычислить площади:

3984. xy =a, x + y =(a>0);

20

3987.(в полярных координатах)

3997. xy = a, xy = 2a, y = x, y =2x, (x > 0, y > 0).

Найти объёмы:

4007. z = 1+ x + y, z = 0, x + y = 1, x = 0, y =0.

4009., y= 1, z = 0.

4018. (переходя к полярным координатам)

4021.

4036. Найти площадь части поверхности az = xy, заключённой внутри поверхности

4037.Найти площадь поверхности тела ограниченного поверхностями

4046. Найти поверхность и объём тела, ограниченного поверхностями , (а > 0).

4052.Найти координаты центра тяжести однородной пластинки x + y= 2a. (a > 0).

4073.Определить силу притяжения однородным цилиндром , материальной точки Р(0,0,b), если масса цилиндра равна М, а масса точки m.

3

Демидович 40(77,78,82,83,91,92), 41(02,03,06,07,33,37,59).

Вычислить тройные интегралы:

4077., V.

4078.V.

4082.Расставить пределы интегрирования различными способами:

21

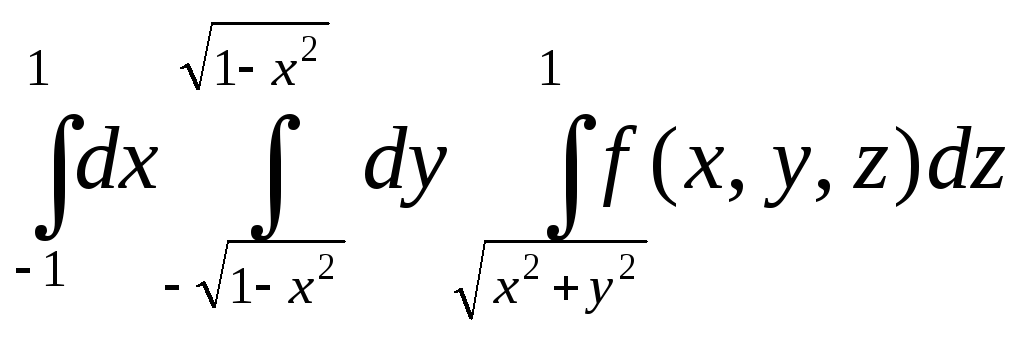
4083.Различными способами расставить пределы интегрирования:

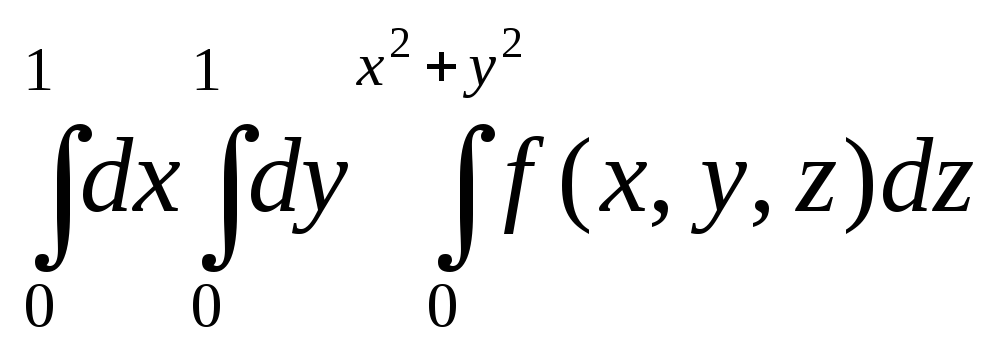
Вычислить:

4091..

Указание: перейти в цилиндрическую систему координат.

4092.

Вычислить объёмы:

4102. z = x + y, z = xy, x + y =1, x = 0, y = 0.

4103.

4106..

4107. x² + y²+ z² = 2az; x² + y²  z².

Найти координаты центра тяжести тел, ограниченных поверхностями:

4133. ; z = c.4137. x² + z² = a², y² + z² = a², z 0.

4159. Найти силу притяжения однородным цилиндром ² + ²  a², 0  h плотности ₀ точки Р(0,0,z) c единичной массой.

Для заметок:

22

*** ДОП. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ И

КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

1.

Демидович. 41(61, 63, 74,76,79,96,97,98), 42(04,09,10).

Исследовать на сходимость несобственные интегралы с бесконечной областью интеграции(0m(x,y)M +);

4161..4163..

4174.Вычислить интеграл:.

4176.Переходя к полярным координатам вычислить:

.

Вычислить:

4179.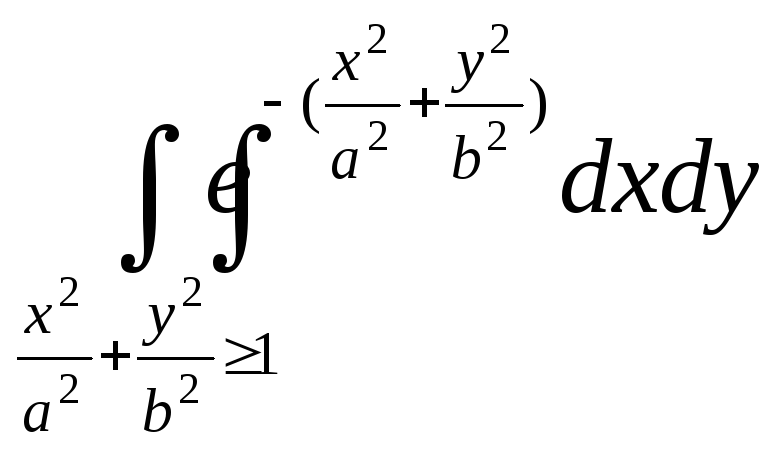.4196..4197..4198..

Вычислить следующие многократные интегралы:

4204. a);

б).

4209.Найти объём n-мерной пирамиды:, (a_i > 0,i= 1, 2,,n).

4210.Найти объём n-мерного конуса, ограниченного поверхностями:

; .

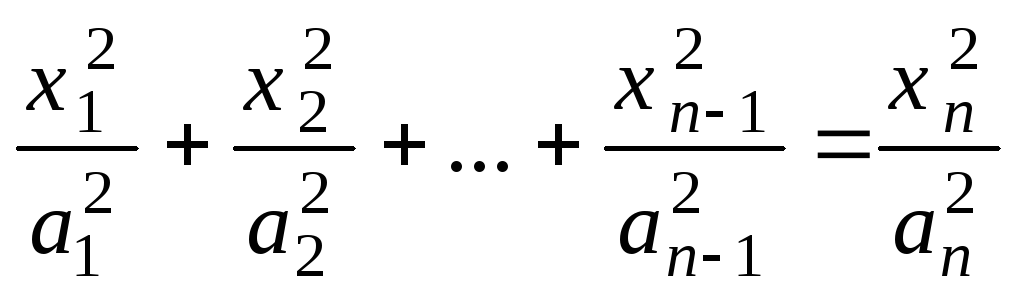23