
Лекции Word Часть1
.pdf1
Уральский федеральный технический университет - УПИ Кафедра “Инженерная графика”
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ ЛЕКЦИИ
Кириллова Татьяна Ивановна
PDF created with pdfFactory Pro trial version www.pdffactory.com
2
ВВЕДЕНИЕ
ИНЖЕНЕРНАЯ ГРАФИКА – общеобразовательная дисциплина состоящая из трех взаимосвязанных разделов: начертательной геометрии, инженерной графики, компьютерной графики.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ - раздел геометрии, который занимается
построением и изучением изображений объектов расположенных в пространстве, графическими методами.
ОБОЗНАЧЕНИЯ И СИМВОЛИКА
Символы обозначающие геометрические фигуры и отношения между ними
1.Геометрическая фигура – Ф;
2.Точки пространства – А, В, С, D, L, M,… 1, 2, 3, 4…; Проекции точек пространства – А1, В2, …11, 12, 13;
3.Линии – а, b, c, d, l, m, n…;
Линии уровня обозначаются –
h – горизонтальная прямая; f – фронтальная прямая;
w – профильная прямая.
Проекции линий – А1В1, А2В2, А3В3; Используются так же обозначения:
AB – прямая, проходящая через точки A и B;
IABI - натуральная величина отрезка или расстояние от точки А до точки В.
4.Плоскости проекций – П1, П2,…Пп;
5.Оси координат – ОX, ОY, ОZ где
X – ось абсцисс, Y – ось ординат, Z – ось аппликат;
6.Плоскости - a, b, g, l, m, h…; проекции плоскостей aП1, bП2, gП3…;
7.Угол – АВС, w°; b°; g°…;
Угловая величина АВС, w - величина угла АВС, w
Символы, обозначающие отношения между геометрическими фигурами
1.= Равны;
2.|| Параллельны;
3.~ Подобны;
4.^ Перпендикулярны;
5.@ Конгруентны;
6.® Отображается;
7.Ç Пересекаются;
PDF created with pdfFactory Pro trial version www.pdffactory.com
3
8. =>Если…..то;
9.X Принадлежит;
10. ÷ Скрещиваются
ОСНОВНЫЕ ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
1.Создание плоской геометрической модели пространственного объекта – чертежа или эпюра). Эпюр – в переводе с греческого – чертеж или проект.
2.Решение задач на плоскости.
3.Создание пространственного объекта - чтение чертежа (эпюра).
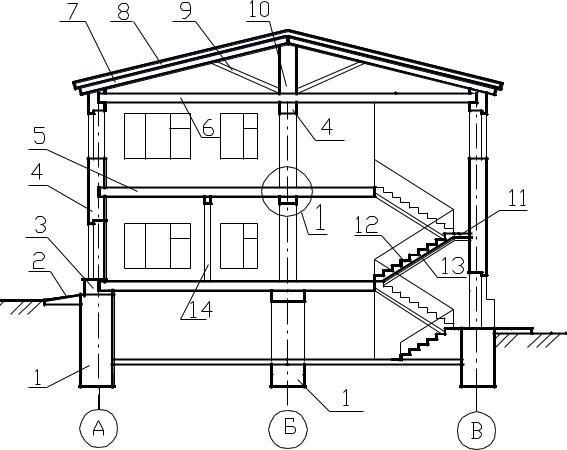
Рис. 1. Пример первой задачи “Начертательной геометрии” |
На чертеже представлен чертеж двухэтажного здания с окнами, дверями, |
лестницами. Представленный чертеж является плоской моделью пространст- |
венного объекта. |
PDF created with pdfFactory Pro trial version www.pdffactory.com
4
ВИДЫ ПРОЕЦИРОВАНИЯ
Графический метод построения изображений пространственных объектов - проецирование. В результате проецирования получаются проекции объектов.
Проецирование – процесс получения на чертеже достоверного изображения, по которому можно представить форму и размеры объекта.
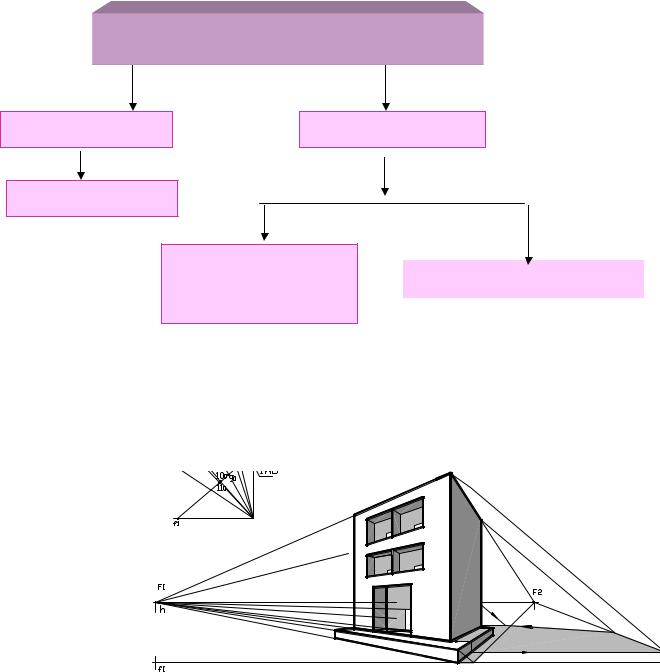
Виды проецирования
Центральное Параллельное
Перспектива
Ортогональное лучи плоскости Аксонометрическое
проекций
Рис. 1. Виды проецирования
Проекция – изображение, полученное проецированием объекта на плоскость или какую-либо другую поверхность. Проекция объекта представляет собой совокупность проекций всех его точек.
Рис. 2 Центральная проекция здания. Перспектива здания
PDF created with pdfFactory Pro trial version www.pdffactory.com
5
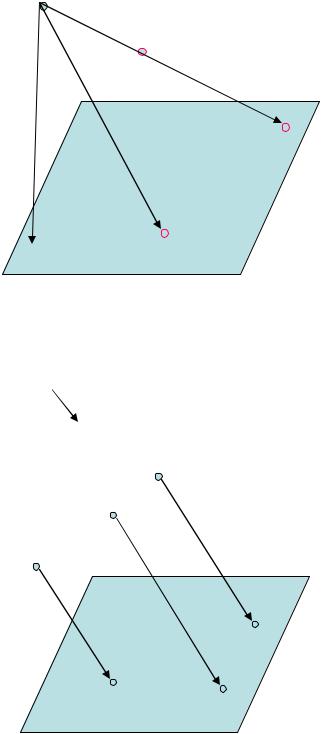
Центральное проецирование
S
А
С 
 В
В
П Ап
 Вп Сп
Вп Сп
Рис. 3. Аппарат центрального проецирования
Параллельное проецирование
s
А
В
С
П
Ап
Сп Вп
Рис. 4. Аппарат параллельного проецирования
1.S – центр проецирования;
2.П – плоскость проекций;
3.А, В, С – точки пространства;
4.SA, SB, SC – проецирующие лучи;
5.Ап, Вп, Сп – проекции точек на плоскости П.
Перспективные изображения получают используя центральное проецирование
1.s – направление проецирования;
2.П – плоскость проекций;
3.А, В, С – точки пространства;
4.ААп, ВВп, ССп – проецирую- щие лучи;
5.Ап, Вп, Сп – проекции точек.
Если проецирующие лучи S перпендикулярны плоскости проекций -
проецирование называется - прямоугольное или ортогональное. -ОРТО- с
древнегреческого переводится как прямой угол. Если проецирующие лучи S
PDF created with pdfFactory Pro trial version www.pdffactory.com
6
наклонены к плоскости проекций под произвольным углом проецирование называется – косоугольное.
Центральное и параллельное проецирование на одну плоскость имеет недостаток:
по одной проекции невозможно однозначно определить положение объекта в пространстве. Для однозначного определения объекта в пространстве Гаспар Монж предложил проецировать на три взаимно перпендикулярные плоскости.
Формирование ортогональной системы плоскостей и координат
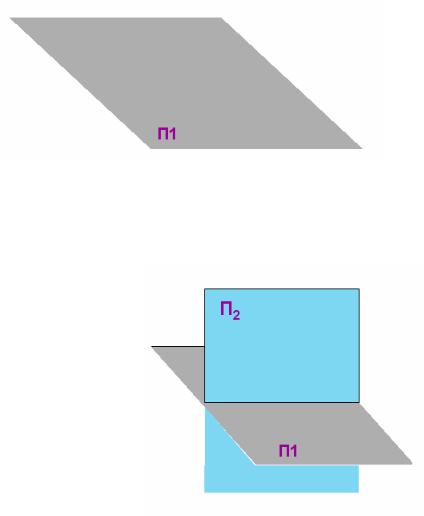
Первая плоскость располагается горизонтально и называется ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ ПРОЕКЦИЙ. Обозначение плоскости - П1
Рис. 5. Горизонтальная плоскость проекций
Вторая плоскость располагается вертикально перед наблюдателем и называется
– ФРОНТАЛЬНАЯ ПЛОСКОСТЬ ПРОЕКЦИЙ. Обозначение плоскости – П2
Рис. 6. Горизонтальная и фронтальная плоскость проекций
Третья плоскость располагается вертикально справа и называется – ПРОФИЛЬНАЯ ПЛОСКОСТЬ ПРОЕКЦИЙ. Обозначение плоскости - П3
PDF created with pdfFactory Pro trial version www.pdffactory.com
7
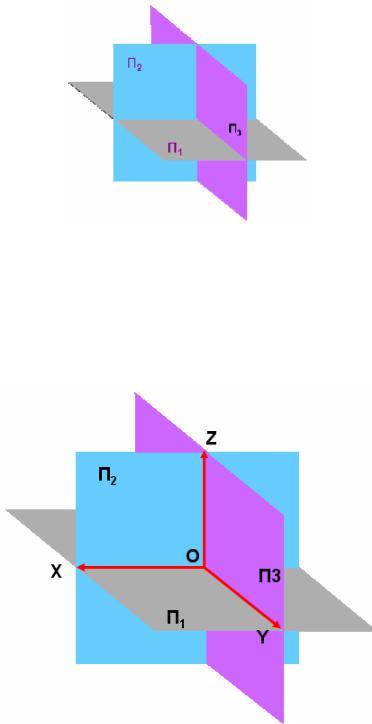
Рис. 7. Горизонтальная, фронтальная и профильная плоскость проекций
Пересекаясь плоскости проекций образуют оси координат: ОX – ось абсцисс;
ОY – ось ординат;
ОZ – ось аппликат.
Точка пересечения осей О - называется начало координат. Место расположе- ния точки в пространстве определяют три координаты (X, Y, Z).
Рис. 8. Ортогональная система плоскостей и осей координат
Введенные плоскости проекций разделяют пространство на восемь октантов: І, ІІ, ІІІ, ІV, V, VІ, VІІ,VІІІ. В первой четверти пространства оси координат имеют положительное направление, поэтому в начертательной геометрии объекты располагают, преимущественно, в первой четверти пространства.
PDF created with pdfFactory Pro trial version www.pdffactory.com
8
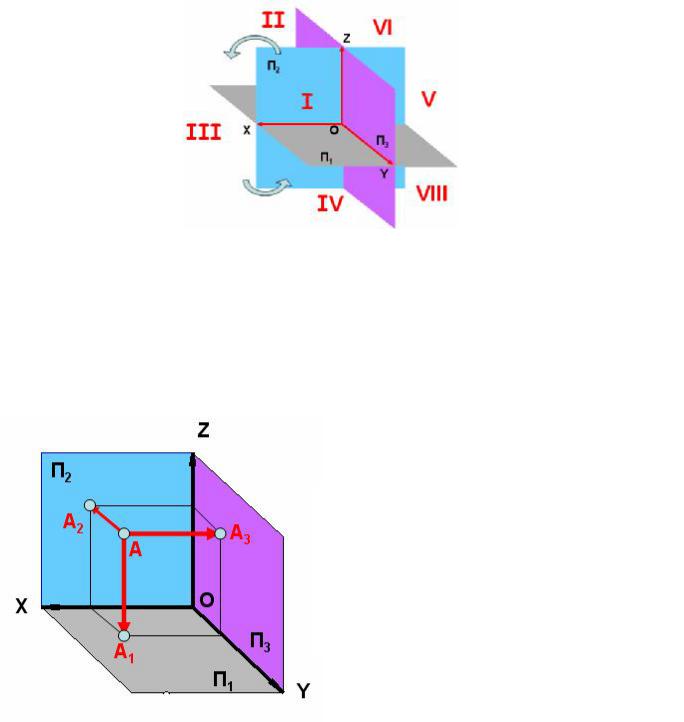
Рис. 9. Октанты пространства
Ортогональные проекции точки
Точка простейший примитив пространства. Проведем проецирующие, перпендикулярные (ортогональные) плоскостям проекций лучи, до пересечения с ними. Точки пересечения ортогональных, проецирующих лучей с плоскостями проекций – ортогональные проекции точек.
А1 - горизонтальная проекция точки А; А2 – фронтальная проекция точки А; А3 – профильная проекция точки А.
Рис. 10. Ортогональные проекции точки
Координаты точки
Координаты точки – это расстояния от точки до плоскости проекций (АА3, АА2, АА1) или от оси координат до проекции точки (AZA2, AXA1, AXA2) как показано на рис. 11. Координаты точки записывают так А(X, Y, Z)
Расстояние АА3 – координата X точки А (XA);
Расстояние AА2 – координата Y точки А (YA);
Расстояние AА1 – координата Z точки А (ZA).
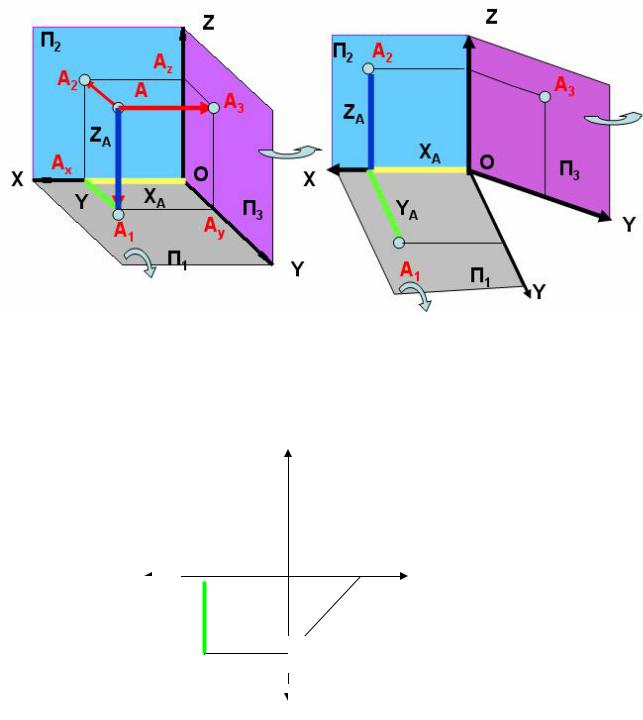
Развернем горизонтальную плоскость П1 и профильную плоскость П3 до совмещения с фронтальной плоскостью П2 (см. рис. 11).
PDF created with pdfFactory Pro trial version www.pdffactory.com
9
Рис. 11. Формирование ортогонального чертежа точки
Фронтальная плоскость П2 не меняет своего положения. Горизонтальная плоскость П1 располагается ниже фронтальной плоскости проекций. Профильная плоскость П3 располагается справа от фронтальной плоскости проекций.
П2
П1X
A2 |
|
|
Z |
|
|
|
||
|
|
|
A3 |
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П3 |
|
|
|
|
|
|
|
|
||
|
|
|
XA |
|
|
|
||
|
|
|
|
|
Y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AY |
|
A |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
АY
A1
Y
Рис. 12. Ортогональный чертеж или эпюр точки
Используя координаты точки XA, YA, ZA строим проекции точки А. По трем координатам строятся горизонтальная и фронтальная проекции точки А. Две проекции, как и три координаты, определяют положение точки в пространстве. Для построения профильной проекции точки нужно провести линии связи: А2А3 , A1А2, АYA3. Построенный чертеж называется ортогональный чертеж точки, или эпюр точки (рис. 12).
Ортогональный чертеж – Эпюр – изображение заданного объекта полученное
путем параллельного прямоугольного проецирования его на две или три взаимно перпендикулярные плоскости проекций (рис. 12).
PDF created with pdfFactory Pro trial version www.pdffactory.com
10
Инвариантные свойства ортогонального проецирования
Инвариантные свойства, это свойства как данного объекта, так и его ортогональных проекций.
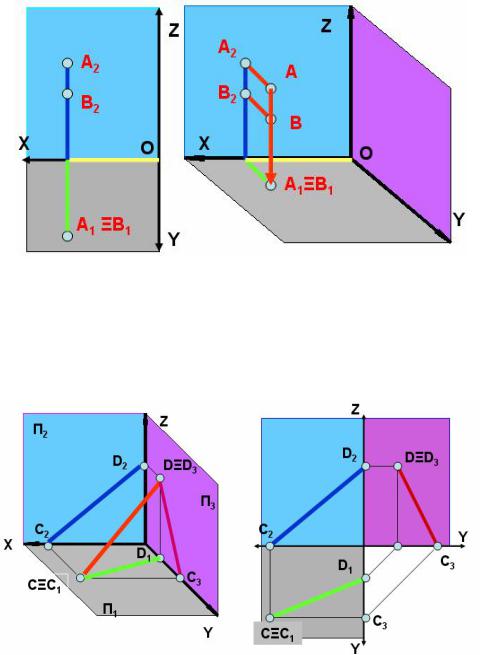
1.Проекция точки есть точка: А → А1, А → А2 (см. рис. 13).
2.Проекции точек лежащих на проецирующем луче совпадают
АВ П1=> А1LВ1 (см. рис. 13).
3.Точка принадлежащая прямой проецируется в точку принадлежащую про- екции этой прямой: А є АВ => А2 є А2В2 (см. рис. 13).
Рис. 13. Инвариантные свойства 1, 2, 3
4.Точки совпадающие с плоскостями проекций проецируютcя сами на себя:
С є П1 => С ≡ С1, D є П3 => D ≡ D3 (см. рис. 14).
5.Проекция прямой есть прямая: СD → C1D1; СD → C2D2, исключение предс- тавляют прямые перпендикулярные плоскостям проекций (см. рис. 14).
Рис. 14. Инвариантные свойства 4 и 5
PDF created with pdfFactory Pro trial version www.pdffactory.com
