
Замятин, задачник по матлогике
.pdfЯсно, что если функция f задана некоторой ДНФ, всякая элементарная конъюнкция этой ДНФ является импликантой функции f.
Если g – элементарная конъюнкция ( не являющаяся литералом), содержащая литерал L, то элементарную конъюнкцию, которая получается из g удалением литерала L, будем обозначать через gL .
Определение. Импликанта g функции f называется простой, если для любого ее литерала L элементарная конъюнкция gL не является импликантой функции f.
Другими словами, простая импликанта – это такая импликанта функции f, которая после удаления любого литерала перестает быть импликантой функции f.
Пример 1 . Пусть функция f задается ДНФ x1 x2 x1 x2 x3 . Убедимся в том, что элементарная конъюнкция g = x1 x2 является простой импликантой функции f. Ясно, что она является импликантой функции f. Если же удалить одну из переменных конъюнкции g, скажем x1 , то получившаяся элементарная конъюнкция g1 = x2 уже не будет импликантой функции f. Действительно, если x1 = 0, x2 = 1, x3 = 0, то g1 = 1 и f = 0 . Итак, g − простая импликанта функции f. Другая импликанта функции f – элементарная конъюнкция h = x1 x2 x3 не является простой, так как после удаления переменной x3 « превращается» в импликанту g.
Импликант у данной функции ( которая не является тождественно ложной) бесконечно много. Действительно, если f – функция от переменных x1 , x2 , … , xn и f( a1 , a2 , … , an ) = 1 для a1 , a2 , … , an {0, 1}, то элементарная конъюнкция x1 a 1 x2 a 2 … xn a n является импликантой функции f. С другой стороны, если g – импликанта функции f и xl – переменная, отличная от переменных функции f и не содержащаяся в элементарной конъюнкции g, то элементарная конъюнкция gxl − импликанта функции f. Осталось напомнить, что множество переменных бесконечно. В то же время множество простых импликант булевой функции конечно, поскольку простая импликанта должна содержать только существенные переменные булевой функции.
Введем основное понятие данного параграфа. Определение. ДНФ называется сокращенной, если она
является дизъюнкцией всех своих простых импликант. Пример 2 . ДНФ g1 = x1 x2 x3 является сокращенной,
так как она имеет только две простых импликанты x1 и x2 x3
160
и является их дизъюнкцией. ДНФ g2 = x1 x2 x1x2 x3 сокра-
щенной не является. Нетрудно проверить, что g2 имеет единственную простую импликанту – переменную x2 .
Как было сказано, цель данного и следующего параграфов – изучить способ нахождения ДНФ, которая задает эту функцию и содержит наименее возможное количество литералов. В качестве первого ( и основного) шага изучим способ построения сокращенной ДНФ по данной булевой функции f.
Мы будем предполагать, что f не является тождест-
венно ложной и задается СДНФ.
Рассмотрим следующие преобразования, применяемые к паре элементарных конъюнкций:
1) xg x g → xg x g g ( неполное склеивание),
2)xg g → g ( поглощение),
3)x g g → g ( поглощение),
где g – элементарная конъюнкция, x − переменная. Применять эти преобразования будем следующим обра-
зом. Пусть исходная СДНФ содержит n переменных. Применяем преобразования 1 – 3 в указанном порядке к элементарным конъюнкциям ранга n до тех пор, пока эти преобразования применимы. Затем их применяем к элементарным конъюнкциям ранга n − 1 и т. д.
Следующее утверждение в литературе называется теоремой Куайна.
Теорема 5 . 7 . Пусть булева функция представлена СДНФ f. Тогда в результате применения к f описанной выше процедуры получается сокращенная ДНФ.
Рассмотрим примеры.
Пример 3 . Пусть
f = x1 x2 x3 x1x2 x3 x1 x2 x3 x1x2 x3 x1 x2 x3 .
Применяя преобразование 1, получаем
f1 = f x2 x3 x1 x2 x1x2 x2 x3 x1 x3 .
Так как элементарные конъюнкции формулы f участвовали в преобразовании 1, после применения преобразований 2 и 3 получим ДНФ
f2 = x2 x3 x1 x2 x1x2 x2 x3 x1 x3 .
Действуем преобразованием 1 на формулу f2 , получим f3 = f2 x2 .
161
После преобразований 2 и 3 формула f3 превратится в формулу
f4 = x1 x3 x2 .
К формуле f4 не применимо ни одно из преобразований
1– 3 . Следовательно, f4 − сокращенная ДНФ формулы f1 .
Пример 4 . Пусть
f = x1 x2 x3 x1x2 x3 x1 x2 x3 x1 x2 x3 .
Применим к формуле f последовательно преобразования 1, 2 и 3, получим формулы
f1 = f x2 x3 x1 x3 x1 x2 , f2 = x2 x3 x1 x3 x1 x2 .
К формуле f2 не применимо ни одно из преобразований
1– 3, следовательно, f2 − сокращенная ДНФ формулы f1 . Этот пример показывает, что преобразование 1 ( непол-
ное склеивание) нельзя заменить на преобразование 1 ′: xg x g → g ( полное склеивание) . Действительно, после проведения преобразования 1 ′, формула f превратилась бы в формулу x2 x3 x1 x2 x3 x1 x2 x3 и дальнейшее применение преоб-
разований 1 ′, 2 и 3 стало бы невозможным.
Напомним, что для проведения преобразований 1 – 3 исходная ДНФ должна быть совершенной. Следующий пример показывает, что это условие существенно.
Пример 5 . Рассмотрим ДНФ
g = x1 x2 x3 x1 x4 x2 x4 .
К ней преобразования 1 – 3 неприменимы. Тем не менее она сокращенной не является, поскольку импликанта x1 x2 x3 не является простой ( можно вычеркнуть переменную x3 ) . Для того, чтобы получить сокращенную ДНФ, эквивалентную g, надо взять СДНФ
h = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4x1 x2 x3 x4 x1x2 x3 x4 x1 x2 x3 x4 x1x2 x3 x4 ,
эквивалентную g, и преобразования 1 – 3 применить к h. В результате получается сокращенная ДНФ x1 x2 x1 x4 x2 x4
эквивалентная g.
Покажем на примерах, как найти сокращенную ДНФ, если исходная булева функция задана картой Карно и на n- мерном кубе
Пример 6 . Пусть булева функция f задана картой Карно на рис. 5 . 9 .
162

|
x3x4 |
|
|
|
|
|
x1x2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
|
|
|
|
|
|
0 0 |
1 |
1 |
|
1 |
|
0 1 |
|
1 |
1 |
|
|
1 1 |
1 |
1 |
1 |
|
|
1 0 |
|
1 |
|
|
Рис. 5.9
Выделим на этой карте максимальные прямоугольники, состоящие из « единиц» и имеющие площадь 2 l клеток для некоторого l. В нашем случае таких прямоугольников будет пять ( см. рис. 5 . 10) .
Напомним, что карта Карно представляет из себя тор, поэтому две « единицы» с « координатами» 0000 и 0010 образуют максимальный прямоугольник требуемой площади. На рисунке он отмечен двумя прямоугольниками « без стороны» . Каждый из максимальных прямоугольников определяет элементарную конъюнкцию, которая указана на рисунке. Этими элементарными конъюнкциями исчерпываются
|
g1=x1x2x4 |
g2=x1x2x3 |
|
Это один |
|
|
|
|
|
|
прямоугольник |
|
x3x4 |
|
|
|
|
|
x1x2 |
0 0 |
0 1 |
1 1 |
1 0 |
g3=x3x4 |
0 0 |
1 |
1 |
|
1 |
0 1 |
|
1 |
1 |
|
|
|
|
g4=x2x4 |
|||
g2=x1x2x3 |
1 1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
1 0 |
|
1 |
|
|
|
|
|
Рис. 5.10 |
|
|
все простые импликанты функции f. Удалим, например, у |
|||||
элементарной конъюнкции g1 = x1 x2 x4 |
последний литерал x4 . |
||||
Получим элементарную конъюнкцию h = x1 x2 , которая уже не |
|||||
будет импликантой функции f. Действительно, если x1 = 0, |
|||||
x2 = 0, x3 = 1, x4 = 1, то h = 1, но f = 0 . Итак, сокращенная |
|||||
ДНФ функции, заданной на рис. 5 . 9, есть дизъюнкция g1 |
|||||
g2 g3 g4 g5 ( см. рис. 5 . 10) . |
|
|
|||
Пример 7 . Функцию f, рассмотренную в предыдущем |
|||||
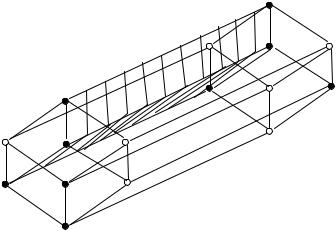
примере, зададим на 4 - х мерном кубе ( см. рис. 5 . 11) . |
|||||
163
|
|
|
1111 |
|
|
|
1011 |
1101 |
1110 |
|
0111 |
1001 |
1010 |
1100 |
|
|
|||
|
|
|
|
|
0011 |
0101 |
0110 |
1000 |
|
|
|
|||
0001 |
0010 |
0100 |
|
|
|
|
|
||
|
0000 |
Рис. 5.11 |
|
|
Пусть Nf = |
{( x1 , x2 , |
x3 , x4 )| f( x1 , x2 , |
x3 , x4 ) |
= 1} . Выделим |
в Nf грани максимальной размерности. Одномерные грани максимальной размерности на рис. 5 . 11 изображены прерывистой линией, двумерные грани максимальной размерности, содержащиеся в Nf , заштрихованы пунктирными линиями. Грани максимальной размерности определяют элементарные конъюнкции, входящие в сокращенную ДНФ.
§ 8. Минимальные ДНФ
Сформулируем, наконец, в явном виде определение минимальной ДНФ, о котором неявно говорилось в предыдущем параграфе.
Определение. ДНФ называется минимальной, если она содержит наименьшее число литералов среди всех ДНФ, ей эквивалентных.
Пример 1 . ДНФ g1 = x1 x2 x3 является минимальной. Убедимся в этом. ДНФ g содержит два литерала. Пусть ДНФ h эквивалентна g1 . Все три переменные ДНФ g1 существенны. Следовательно, h должна содержать эти переменные. Но это означает, что h содержит, по крайней мере, три литерала. Итак, ДНФ g1 является минимальной.
ДНФ g2 = x1 x1x2 минимальной не является, так как она эквивалентна ДНФ x1 x2 , содержащей меньше литералов.
Предложение. Минимальная ДНФ состоит из простых импликант.
Доказательство. Докажем, что всякая минимальная ДНФ является дизъюнкцией своих простых импликант. Пусть минимальная ДНФ f равна g1 g2 … gk , где g1 , g2 ,
164
… , gk – элементарные конъюнкции, и одна из этих элементарных конъюнкций, скажем g1 , не является простой импликантой функции, определяемой формой f. Тогда существует литерал, после вычеркивания которого g1 остается импликантой функции f. Можно считать, что этот литерал является переменой x. Это означает, что g1 = g1 ′x и g1 ′ – импликанта функции f. Рассмотрим ДНФ f′ = g1 ′ g2 … gk . Убедимся в том, что и f эквивалентны. Переменным ДНФ f придадим некоторые значения. Если f = 1 при этих значениях переменных, то очевидно, что f′ = 1 при тех же значениях переменных. Пусть теперь f′ = 1 . Тогда одна из элементарных конъюнкций g1 ′, g2 , … или gk принимает значение 1 . Если gi = 1 при 2 ≤ i ≤ k, то f = 1, так как f содержит gi . Если же g1 ′ = 1, то попрежнему f = 1, поскольку g1 ′ – импликанта f. Итак, ДНФ f и f′ эквивалентны. Это противоречит тому, что f − минимальная ДНФ, так как f′ содержит на один литерал меньше. Следовательно, все элементарные конъюнкции ДНФ f являются ее простыми импликантами.
В предыдущем параграфе мы отмечали, что первым шагом к получению минимальной ДНФ, задающей данную функцию, является нахождение сокращенной ДНФ. Вторым шагом к этому является нахождение ядра сокращенной ДНФ. Дадим соответствующие определения.
Определение. Пусть g и h элементарные конъюнкции. Будем говорить, что g покрывает h, если любой литерал из g содержится в h.
Другими словами, элементарная конъюнкция g покрывает элементарную конъюнкцию h, если g является импли-
кантой h. Например, g1 = x1 x2 покрывает h = x1 x2 x3 , а g1 = x1x2 не покрывает h.
Определение. Простая импликанта называется ядровой, если она покрывает некоторую элементарную конъюнкцию исходной СДНФ, не покрываемую другой простой импликантой. Множество ядровых импликант называется ядром сокращенной ДНФ.
Из пяти простых импликант сокращенной ДНФ, заданной на рис. 5 . 10, все, кроме g2 , являются ядровыми.
Отметим, что ядро сокращенной ДНФ может быть пустым, а может содержать все простые импликанты ( см. рис. 5 . 12 и 5 . 13) .
165

x2x3 |
0 0 |
0 1 |
1 1 |
1 0 |
|
x1 |
|||||
|
|
|
|
||
0 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
|
|
Рис. 5.12 |
|
|
||
x2x3 |
0 0 |
0 1 |
1 1 |
1 0 |
|
x1 |
|||||
|
|
|
|
||
0 |
|
1 |
1 |
1 |
|
1 |
|
|
1 |
|
|
Рис. 5.13
Изложим третий, завершающий шаг способа нахождения минимальных ДНФ. Покажем, как находятся так называемые тупиковые ДНФ, а из них уже простым перебором – минимальные ДНФ.
Определение. Простая импликанта называется избыточной, если ее можно удалить без потери эквивалентности исходной СДНФ.
Пример 2 . Рассмотрим функцию f, задаваемую картой Карно на рис. 5 . 14 .
|
g2=x2x3x4 |
g5=x1x2 |
|
g4=x3x4 |
g3=x1x2x4 |
|
|
x3x4 |
|
|
|
|
|
|
|
|
|
|
|
|
g1=x1x3x4 |
x1x2 |
0 0 |
0 1 |
1 1 |
1 0 |
|
|
0 0 |
1 |
|
|
1 |
|
|
0 1 |
1 |
1 |
1 |
1 |
|
|
1 1 |
|
|
1 |
1 |
|
|
1 0 |
1 |
1 |
|
1 |
g8=x1x2x4 |
|
g7=x1x2x3 |
|
Рис. 5.14 |
g6=x2x3 |
|
|
Как видно на рисунке, сокращенная ДНФ содержит 8 простых импликант. Ядро сокращенной ДНФ состоит из трех простых импликант: g5 , g6 и g7 . Остальные импликанты являются избыточными. Каждую из них можно удалить без потери эквивалентности СДНФ, задающей функцию f.
166
Определение. ДНФ, состоящая из простых импликант исходной СДНФ, содержащая все ядровые импликанты и не содержащая ( своих) избыточных импликант, называется ту-
пиковой.
Например, ДНФ g1 g4 g5 g6 g7 и g3 g5 g6 g7g8 являются тупиковыми ( см. рис. 5 . 14) .
Сформулируем очевидное Предложение 2 . Всякая минимальная ДНФ является ту-
пиковой.
Задачу нахождения минимальных ДНФ, задающих данную булеву функцию можно решить следующим образом. Сначала найти все тупиковые ДНФ ( их, как правило, оказывается немного) . Затем простым просмотром выбрать их них минимальные.
Тупиковая ДНФ получается из сокращенной удалением максимального количества избыточных импликант сокращенной ДНФ так, чтобы сохранилась эквивалентность исходной СДНФ.
На примере булевой функции f, заданной картой Карно на рис. 5 . 14, покажем, как это можно сделать. Тупиковая ДНФ должна содержать дизъюнкцию ядровых импликант, т. е. g5 g6 g7 . Этой дизъюнкцией не покрываются три единицы карты, которые получаются при следующих наборах значений аргументов: 0000, 0010, 1010 . Составим таблицу, строки которой индексируются этими наборами, а столбцы
– избыточными импликантами сокращенной ДНФ ( см. таб-
лицу 5 . 7) .
Таблица 5 . 7
|
g 1 |
g 2 |
g 3 |
g 4 |
g 8 |
0 0 0 0 |
+ |
+ |
+ |
|
|
0 0 1 0 |
|
|
+ |
+ |
|
1 0 1 0 |
|
|
|
+ |
+ |
В клетках таблицы ставим знак «+», если единица карты покрывается импликантой. В противном случае клетку оставляем пустой. Надо найти все минимальные подмножества столбцов, « плюсы» которых покрывают все строки. В нашем примере такими подмножествами будут следующие: { g1 , g4 }, { g2 , g4 }, { g3 , g4 }, { g3 , g8 } . Следовательно, булева функция имеет четыре тупиковых ДНФ:
h1 = g5 g6 g7 g1 g4 , h2 = g5 g6 g7 g2 g4 , h3 = g5 g6 g7 g3 g4 , h4 = g5 g6 g7 g3 g8 .
167
ДНФ h1 , h2 , h4 являются минимальными, все они содержат по 12 литералов. ДНФ h3 содержит 13 литералов, и поэтому не является минимальной.
§ 9. Функции k-значной логики. Способы задания
Напомним, что k – натуральное число, большее 1 ( число истинностных значений), и Bk = {0, 1, … , k– 1} .
Определение. Функцией k-значной логики называется
( всюду определенная) функция вида
f: Bk n → Bk ,
где n – число аргументов ( переменных), Bk n – декартова степень множества Bk .
Другими словами, функция k- значной логики – это отображение множества n- элементных последовательностей, составленных из элементов множества {0, 1, … , k– 1}, в это множество. Допускается случай n = 0; такие функции называются константами. Класс всех функций k- значной логики обозначается через Pk .
Как и в случае булевых функций, будем считать, что − зафиксировано бесконечное множество переменных
( аргументов),
− если дана функция k- значной логики, то зафиксировано обозначение ее переменных.
Функцию из Pk от n переменных можно задать таблицей, содержащей n+1 столбец. В первых n строках таблицы записываются всевозможные наборы значений аргументов. Нетрудно понять, что таких наборов будет kn . Следовательно, число всех функций от переменных x1 , x2 , … , xn равно km , где m = kn . Указанное число является очень большим. Например, число функций от переменных x1 , x2 3 - значной логики равно 3 9 = 19683 . В силу этого, возникают ( в отличие от булева случая) трудности при использовании табличного задания функций, и такой способ задания обычно не применяется.
Функции k- значной логики мы будем задавать термами некоторой сигнатуры. Приведем список конкретных функций из Pk , которые можно считать элементарными функциями. Функции, которые мы будем рассматривать в дальнейшем, будут суперпозициями элементарных функций. Та-
168

ким образом, имена функций из списка и составят сигнатуру.
1 . ¬x = x + 1 ( mod k) . При k = 2 функция ¬x совпадает с обычным отрицанием, т. е. функция является обобщением отрицания в двузначной логике. Мы будем называть ее цик-
лическим отрицанием.
2 . x = ( k – 1) – x. Как и предыдущая, функция x является обобщением обычного отрицания. Она называется от-
рицанием Лукасевича.
На рисунках 5 . 15 и 5 . 16 приведены графики функций ¬x
и x соответственно при k =6 . |
x |
¬x |
|
5 |
5 |
1 |
|
|
1 |
|
|
0 1 |
5 |
x |
0 1 |
5 |
x |
Рис. 5.15 |
|
Рис. 5.16 |
|
|
|
3 . Пусть 0 ≤ l ≤ k. Следующую функцию будем называть |
|||||
малой характеристической функцией числа l: |
|
|
|||
1, если x = l, |
|
|
|
||
jl ( x) = |
если x |
≠ l. |
|
|
|
0, |
|
|
|
||
4 . Пусть, как и выше, 0 ≤ l ≤ k. Функцию Jl ( x), определенную ниже, будем называть большой характерис-
тической функцией числа l:
k- 1, если x = l, |
|
Jl ( x) = |
|
0, если x ≠ l. |
|
На рисунках 5 . 17 и 5 . 18 |
приведены графики функций |
j2 ( x) и J2 ( x) соответственно при k =6 . |
|
j 2 ( x ) |
J 2 ( x ) |
5 |
5 |
1 |
|
|
|
1 |
|
|
|
0 |
1 |
5 |
x |
0 |
1 |
5 |
x |
|
|
Рис. 5.17 |
|
|
|
Рис. 5.18 |
|
5 . min( x1 , x2 ) . Функцию можно считать обобщением конъюнкции. Иногда будем ее обозначать через x1 & x2 .
169
