
Chast_8_Teoria_polya
.pdfМинистерство образования и науки Российской Федерации Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина
МАТЕМАТИКА
Часть 8. ТЕОРИЯ ПОЛЯ
Екатеринбург
УрФУ
2012
Министерство образования и науки Российской Федерации Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина
МАТЕМАТИКА
Часть 8. ТЕОРИЯ ПОЛЯ
Научный редактор – доц., канд. физ.-мат. наук Л.П. Мохрачева
Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов специальностей направления 270800 «Строительство» всех форм обучения
УДК 511.236(075.8) ББК 22.132 я 73 Т 11
Рецензенты:
кафедра физики Уральского государственного лесотехнического университета; доктор физ-мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН
Авторы: М.А. Вигура, О.А. Кеда, Е.М. Пампура, А.Ф. Рыбалко, Н.М. Рыбалко
Часть 8. ТЕОРИЯ ПОЛЯ: учебное пособие / М.А. Вигура, О.А. Кеда, Е.М. Пампура, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2008. 118 с.
ISBN
Данное пособие представляет собой восьмую часть курса высшей математики и предназначено для бакалавров, программа обучения которых предусматривает равные количества аудиторных часов и часов для самостоятельной работы студентов.
В пособии излагаются основные положения теории поля (векторного анализа) и ее приложений, в которых изучаются скалярные и векторные поля. Пособие включает также примеры решения задач, текст домашних заданий, пример оформления и задания индивидуальных расчетных работ, образец контрольной работы и справочный материал по теме.
Подготовлено кафедрой высшей математики
УДК 517.37(075.8) ББК 22.161.1 я 73
ISBN |
© УРФУ, 2012 |
ОГЛАВЛЕНИЕ |
|
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ПОЛЯ |
|
(ВЕКТОРНОГО АНАЛИЗА) .............................................................................. |
4 |
1.1. Скалярное поле.............................................................................................. |
5 |
1.2. Поверхности и линии уровня........................................................................ |
5 |
1.3. Производная по направлению ...................................................................... |
6 |
1.4. Градиент скалярного поля ............................................................................ |
7 |
1.4.1. Оператор Гамильтона (набла) ........................................................... |
7 |
1.4.2. Связь производной по направлению с градиентом.......................... |
8 |
1.4.3. Свойства градиента............................................................................ |
8 |
1.5. Векторное поле............................................................................................ |
10 |
1.5.1. Векторные линии ............................................................................. |
11 |
1.5.2. Плоское векторное поле .................................................................. |
11 |
2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.................................................................. |
12 |
2.1. Односторонние и двусторонние поверхности ........................................... |
12 |
2.2. Площадь поверхности................................................................................. |
13 |
2.3. Система координат и ориентация поверхности......................................... |
14 |
2.4. Поверхностный интеграл 1-го рода............................................................ |
15 |
2.4.1. Вычисление поверхностных интегралов 1-го рода........................ |
15 |
2.5. Поверхностный интеграл 2-го рода............................................................ |
17 |
3. ПОТОК ВЕКТОРНОГО ПОЛЯ ......................................................................... |
18 |
3.1. Определение потока векторного поля........................................................ |
18 |
3.2. Свойства потока .......................................................................................... |
19 |
3.3. Вычисление потока ..................................................................................... |
19 |
3.3.1. Проектирование на одну координатную плоскость....................... |
20 |
3.3.2. Проектирование на три координатные плоскости ......................... |
20 |
3.4. Физический смысл потока .......................................................................... |
22 |
3.5. Дивергенция векторного поля .................................................................... |
24 |
3.5.1. Свойства дивергенции..................................................................... |
24 |
3.5.2. Физический смысл дивергенции..................................................... |
25 |
3.6. Физический смысл потока через замкнутую поверхность ....................... |
25 |
3.7. Теорема Остроградского - Гаусса .............................................................. |
26 |
3.8. Инвариантное определение дивергенции .................................................. |
29 |
4. ЛИНЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛЕ ......................................... |
29 |
4.1. Понятие линейного интеграла .................................................................... |
29 |
4.2. Свойства линейного интеграла................................................................... |
30 |
4.3. Вычисление линейного интеграла.............................................................. |
30 |
4.4. Физический смысл линейного интеграла .................................................. |
31 |
4.5. Ротор (вихрь) векторного поля................................................................... |
31 |
4.6. Свойства ротора (вихря) ............................................................................. |
32 |
4.7. Теорема Стокса............................................................................................ |
33 |
4.8. Инвариантное определение ротора ............................................................ |
35 |
3
|
4.9. Физический смысл ротора .......................................................................... |
36 |
|
4.10. Формула Грина .......................................................................................... |
37 |
5. |
СПЕЦИАЛЬНЫЕ ВИДЫ ВЕКТОРНЫХ ПОЛЕЙ............................................ |
38 |
|
5.1. Потенциальное векторное поле .................................................................. |
38 |
|
5.1.1. Условия потенциальности поля ...................................................... |
38 |
|
5.1.2. Вычисление потенциала поля ......................................................... |
40 |
|
5.2. Соленоидальное поле.................................................................................. |
41 |
|
5.2.1. Свойства соленоидального поля ..................................................... |
41 |
|
5.3. Операторы Гамильтона и Лапласа ............................................................. |
42 |
|
5.3.1. Оператор Гамильтона (набла) ......................................................... |
42 |
|
5.3.2. Оператор Лапласа ............................................................................ |
43 |
6. |
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ........................................................................... |
45 |
7. |
ДОМАШНИЕ ЗАДАНИЯ.................................................................................. |
72 |
8. |
РАСЧЕТНАЯ РАБОТА ..................................................................................... |
76 |
9. |
ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ........................................................ |
108 |
10. БИБЛИОГРАФИЧЕСКИЙ СПИСОК ........................................................... |
114 |
|
4

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ПОЛЯ (ВЕКТОРНОГО АНАЛИЗА)
1.1. Скалярное поле
ОПРЕДЕЛЕНИЕ. Если с каждой точкой P(x, y, z) некоторой пространственной области G связана скалярная величина, то говорят, что в области G задано скалярное поле: u f (x, y, z) , где f (x, y, z) - скалярная функция, называемая
функцией поля.
Примеры скалярных полей: поле температур, поле давления, поле плотности, поле концентраций, поле электрического потенциала. Рассмотрим подробнее последний пример.
Пусть речь идет о точечном заряде q. Потенциал электростатического поля заряда q, помещенного в начало координат, задается в каждой точке простран-
ства r(x, y, z) , за исключением начала координат, функцией поля вида:
|
|
|
|
u |
|
q |
|
|
q |
|
|
q |
||
|
|
|
|
|
|
|
|
|
|
. |
||||
r |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
r |
|
|
x2 y2 z2 |
|||
Заметим, что если |
|
r |
|
const , |
x2 |
y2 |
z2 |
const - уравнение сферы. Следова- |
||||||
|
|
|||||||||||||
тельно, в точках, принадлежащих сфере, потенциал электростатического поля сохраняет свое значение, или u const .
Ограничимся рассмотрением так называемых стационарных полей, т.е. полей, не зависящих от времени.
1.2. Поверхности и линии уровня
В дальнейшем, если не оговорено особо, предполагаем функцию однозначной и непрерывно-дифференцируемой.
Рассмотрим точки области, в которой функция u f (x, y, z) принимает постоянные значения: f (x, y, z) c (c const) . Это уравнение можно рассматривать как уравнение некоторой поверхности в пространстве.
ОПРЕДЕЛЕНИЕ. Геометрические места точек P(x, y, z) , где скалярное поле принимает одно и то же значение f (x, y, z) c , называются поверхностями уровня или эквипотенциальными поверхностями.
В силу однозначности функции u f (x, y, z) поверхности уровня, соответствующие различным значениям c, не пересекаются между собой.
Скалярное поле называется плоским, если при подходящем выборе системы координат функция поля зависит только от двух переменных. Множество точек плоскости P(x, y) , для которых f (x, y) c , называется линией уровня плоского скалярного поля.
5
Например, линиями уровня поля температур бесконечной равномерно нагретой нити являются окружности
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
|
1.3. Производная по направлению |
|
|
|
|
||||||||||
Пусть в |
пространственной |
|
области |
|
|
|
G |
задано |
скалярное |
поле: |
||||||
u u(x, y, z) u(P) . |
Рассмотрим точку P1(x, y, z) |
и исходящий из нее вектор |
||||||||||||||
l lx ;ly ;lz . Найдем, |
как изменяется поле в направлении вектора l . Сместимся |
|||||||||||||||
из точки P1(x, y, z) в направлении вектора l |
|
в точку |
P2 (x x, y y, z z). |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Обозначим за |
длину вектора |
PP : ρ |
|
PP |
|
, тогда |
ρ |
|
x2 y2 |
z2 . |
||||||
|
|
|||||||||||||||
|
|
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
При этом функция поля получит приращение
u u(P2 ) u(P1) u(x x, y y, z z) u(x, y, z)
|
du ε x ε |
y ε |
z |
u |
|
x |
u |
y |
u |
z θ( ρ) |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 |
|
|
2 |
|
3 |
|
|
x |
|
|
y |
|
|
|
z |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где θ( ρ) - бесконечно малая более высокого по- |
x |
||||||||||||||||||||||||||||||||
рядка по ρ, |
ε1,ε2 ,ε3 0 при x, y, |
z 0 |
, а ве- |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
личина |
|
u |
|
V - средняя скорость изменения ска- |
|
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
ρ |
cp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
лярной функции u(P) в направлении вектора l . |
|
||||||||||||||||||||||||||||||||
|
u |
|
u |
|
x |
|
u |
|
y |
|
u |
|
z |
|
x |
|
|
y |
|
|
z |
. |
|
||||||||||
|
|
|
|
y |
z |
|
|
|
|
||||||||||||||||||||||||
|
|
x |
|
1 |
2 |
3 |
|
||||||||||||||||||||||||||
Перейдем к пределу при 0,что соответствует стремлению
P1 P2  l
l

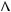 y
y
P P:
2 1
|
|
|
|
|
|
|
lim |
u |
|
u |
cosα |
u |
cosβ |
u |
cos γ |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|
x |
y |
z |
|
|
|
|
|
|
|
|||||||
где |
cos , |
cos , |
cos |
- |
направляющие косинусы вектора |
PP . |
|
Поскольку |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
PP |
|
l , то |
их направляющие косинусы равны. |
Так как |
l l |
i l |
y |
j l |
k , то |
|||||||||||||||||
|
||||||||||||||||||||||||||
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
z |
|
|
|
|
|
l |
x |
|
ly |
|
|
|
l |
z |
|
|
|
|
|
|
|
|
|
|
|
||||
cos |
|
, cos |
|
, cos |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
| l | |
|
| l | |
|
| l | |
|
|
|
|
|
|
|
|
|
|
|
||||||||
6

ОПРЕДЕЛЕНИЕ. Производной функции u в точке P(x, y, z) (обозначение u )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
по направлению вектора l |
|
|
|
|
|
|
|
|
u |
||||||||||
называется предел lim |
|
(если он существует), |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 0 |
l |
||||
равный |
u |
lim |
u |
|
u |
cos |
u |
cos |
u |
cos . |
|
|
|
|
|||||
l |
l |
|
|
|
|
|
|
|
|||||||||||
|
l 0 |
|
x |
|
y |
|
|
z |
|
|
|
|
|||||||
Производная по направлению l : |
u |
- определяет скорость изменения ска- |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
u |
|
|||||
лярного поля в направлении вектора l , |
в частности, если |
>0, поле возраста- |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
||
ет, если u <0, поле убывает.
l
ПРИМЕР. Найдите производную u в точке Р (1,1,1) в направлении вектора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
||
i j k , |
если u x2 |
y2 z 2 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ux |
|
P 2 x |
|
P 2, uy |
|
|
P 2 y |
|
|
P 2, uz |
|
P 2 z |
|
P 2 ; |
|
|
|
|
|
, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||
cos α |
1 |
|
;cosβ |
|
1 |
|
;cos γ |
1 |
|
|
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
1 |
2 |
1 |
2 |
1 |
|
|
|
6 |
|
0 , следовательно, скалярное поле возрастает. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
3 |
3 |
3 |
3 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1.4. Градиент скалярного поля
Пусть задано скалярное поле u(x,y,z)=u.
ОПРЕДЕЛЕНИЕ. Градиентом скалярного поля u в точке P(x, y, z) на-
зывается вектор, обозначаемый символом grad u и определяемый равенством
|
u |
u |
u |
|||
grad u |
|
i |
|
j |
|
k |
|
|
|
||||
|
x |
y |
z |
|||
1.4.1. Оператор Гамильтона (набла)
Введем символический вектор “набла” или оператор Гамильтона
|
|
|
|
|
|
|
|
|
|
|
|||
i |
|
j |
|
k |
|
|
|
; |
|
; |
|
. |
|
x |
y |
z |
|
|
|
||||||||
|
|
|
|
|
x y |
|
y |
||||||
Знак - используется для записи операций векторного анализа в сокращенной и удобной для расчётов форме.
7

Выражение вида u(x, y, z) понимается как результат действия оператора на соответствующую функцию.
Тогда
|
|
|
|
|
u |
u |
u |
|
|
|
|
||||||||
u(x, y,z) (i |
|
|
j |
|
|
k |
|
) u(x, y,z) |
|
i |
|
j |
|
k |
j |
||||
|
|
|
|
uxi |
uy |
uz k , |
|||||||||||||
|
|
x |
|
y |
|
z |
x |
y |
z |
|
|
|
|
||||||
grad u u .
1.4.2. Связь производной по направлению с градиентом
|
|
|
|
u |
|
|
u |
cos |
u |
cos |
u |
cos . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
y |
z |
|
|||||||||||||||||
|
|
Пусть l0 (cos ,cos ,cos ) - единичный вектор |
|
||||||||||||||||||||||||||||
(орт) в направлении l , тогда видно, что |
|
||||||||||||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( u l ) |
u |
|
l |
cos |
grad u |
cos , |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где - угол между единичным вектором l0 данного направления l |
и вектором |
||||||||||||||||||||||||||||||
градиента grad u . |
|
|
|
|
|
u |
|
|
|
|
u |
|
|
|
|
|
|
||||||||||||||
|
|
Если grad u 0 , то |
|
0. Если grad u 0 , то |
|
|
grad u |
|
|
для всех век- |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
l |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
торов l |
, за исключением вектора l , направленного в сторону grad u . |
||||||||||||||||||||||||||||||
|
|
Вывод: |
|
u |
|
|
grad u |
|
cos . Производная по направлению вектора l в точ- |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
ке P(x, y, z) |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
равна проекции градиента на данное направление. |
|
||||||||||||||||||||||||||||||
1.4.3. Свойства градиента
Пусть задан градиент поля и производная по направлению:
|
|
u |
|
u |
|
u |
|
|
|
u 2 |
|
u 2 |
|
u 2 |
|
||||
|
|
|
|
|
|||||||||||||||
u |
|
|
, |
|
, |
|
, |
u |
= |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
y |
|
z |
|
|
x |
|
y |
z |
|
||||||
|
|
|
|
|
|
||||||||||||||
1. Максимальное значение производной по направлению равно модулю гради-
ента: |
u |
|
|
gradu |
|
cos ; 0;cos 1 max |
u |
|
|
grad u |
|
. |
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.Вектор u направлен в сторону возрастания поля.
3.Вектор u всегда нормален к поверхности (линии) уровня поля (эквипотенциальной поверхности).
8
Доказательство:
Пусть u u(x, y, z) скалярное поле и u(x, y, z) c - уравнение поверхно-
сти уровня. Выберем P u(x, y, z) c , которую обозначим P(x, y, z) , и проведём касательную плоскость к поверхности, описываемой уравнением
F (x, y, z) u(x, y, z) c 0 ;
F (x x) F (y y) F (z z) 0 - уравнение касательной плоскости;
x |
y |
z |
|
|
|
|
|
|
|
||||
|
|
u |
(x |
|
) |
u |
(y |
|
) |
u |
(z |
|
) 0 . |
|
|
x |
y |
z |
|||||||||
|
|
x |
y |
|
|||||||||
|
|
|
|
|
|
|
|
z |
|||||
Тогда вектор нормали касательной плоскости имеет вид:
|
u |
|
u |
|
u |
u |
u |
u |
|
||||||
n |
|
, |
|
, |
|
|
, n |
|
i |
|
j |
|
k u . |
||
x |
|
|
|
|
|
||||||||||
|
|
y |
|
z |
|
x |
y |
z |
|
||||||
Свойства 1-3 дают инвариантное (не зависящее от системы координат) определение градиента, т.е. утверждают, что независимо от системы координат u указывает величину и направление наибольшего возрастания скалярного поля в
u
точке: grad u max .
l
Дифференциальные свойства градиента:
Если скалярное поле есть сумма двух полей
f(x, y, z) u(x, y, z) v(x, y, z) , то f (u v) u v .
(u v) ( u)v u( v) .
c u c u .
f (u) fu u - градиент сложной функции.
f (u,v) fu u fv v .
ПРИМЕР. Найдите наибольшую крутизну подъёма поверхности u x y
в точке Р (2,2,4).
Решение: grad u max u .
l
u ux i u y j uz k = yx y 1 i x y ln x j 0k . |
|
|
||
|
( yx y 1 )2 (xy ln x)2 |
(2 2)2 (4ln 2)2 |
4 |
1 ln2 2 . |
u |
||||
9
