9.10. Вычисление площади поверхности вращения

Пусть функция f(x) неотрицательна и непрерывна вместе со своей производной на отрезке [a,b]. Тогда площадь поверхности, образованная вращением графика этой функции вокруг оси Ox, будет вычисляться по формуле:

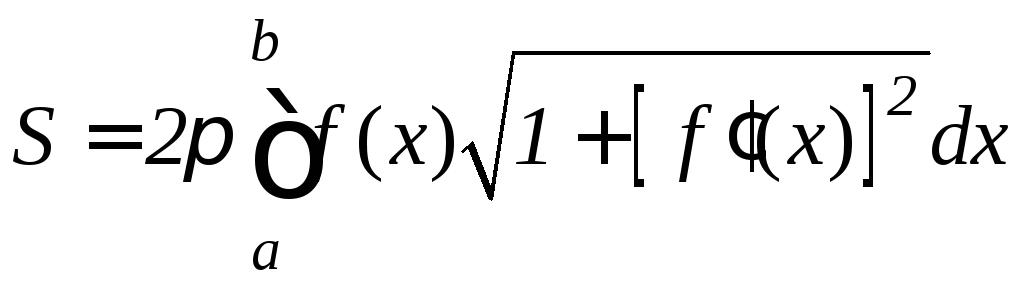. (9.14)

Пример 14. Вычислить площадь поверхности, образованной вращением вокруг оси Ox: а) отрезка прямой ; б) одной арки синусоидыy=sin x ; в) одной арки циклоиды x=a(t–sint), y=a(1–cost) ; г) параболы y²=2px, 0xa; д) дуги окружности x²+y²=R².

Решение. а) Вычислим площадь поверхности, полученной вращением отрезка прямой вокруг осиOx (рис. 9.16). Найдем производную: . Подставляя в формулу (9.14) получим:

.

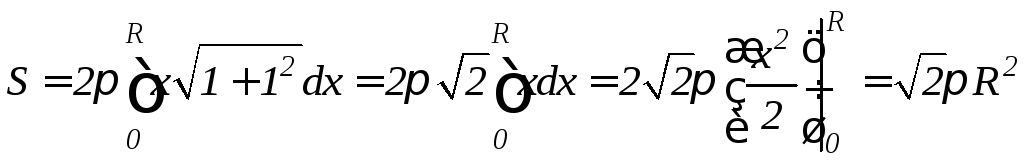б) Согласно формуле (9.14), получим

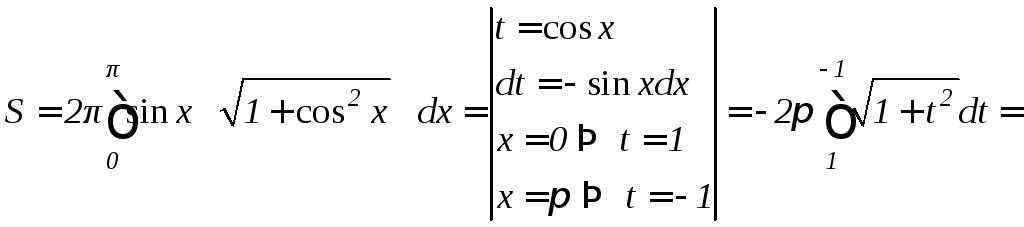
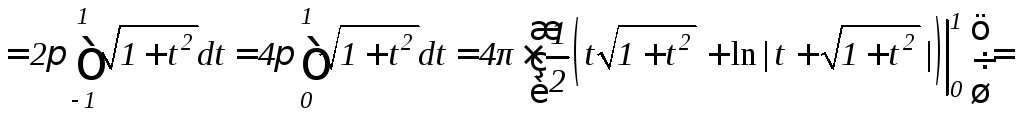
(ед.кв.).

Замечание. При вычислении интеграла 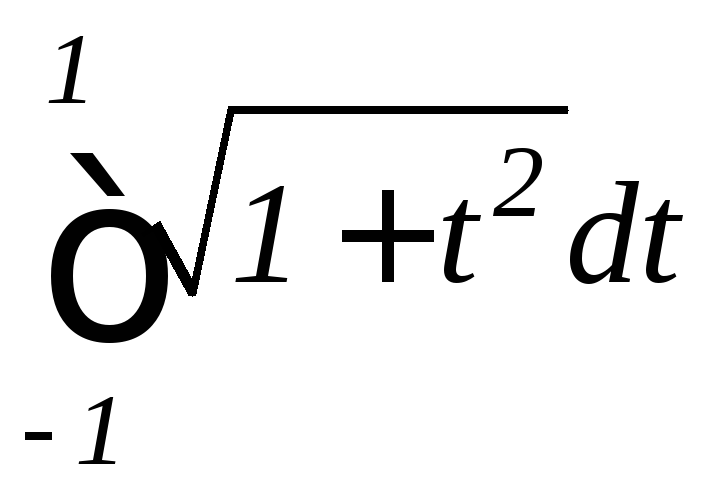было использовано свойство 4 определенного интеграла (см. 9.2) и табличный интеграл(отметим, что этот интеграл можно было найти и методом интегрирования по частям).

в) В параметрической форме формулу (9.14) можно записать в следующем виде:

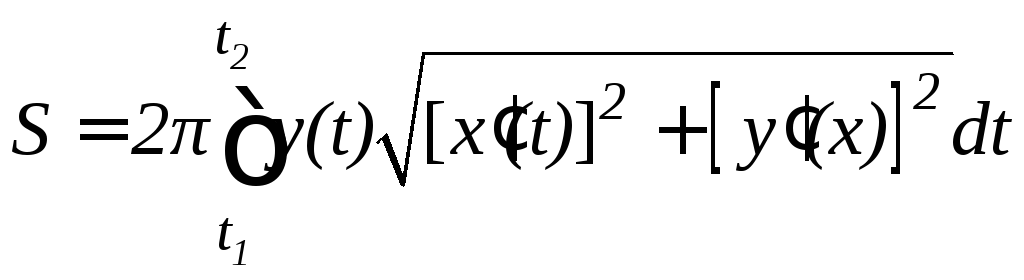. (9.15)

Тогда площадь поверхности, образованной вращением одной арки циклоиды вокруг оси Ox, будет равна

.

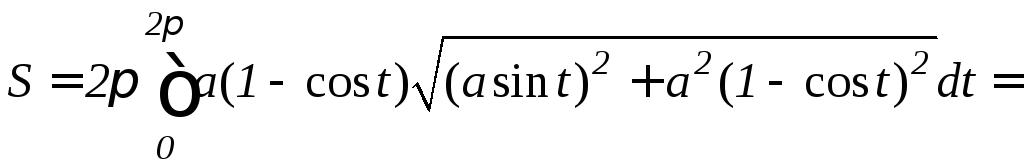
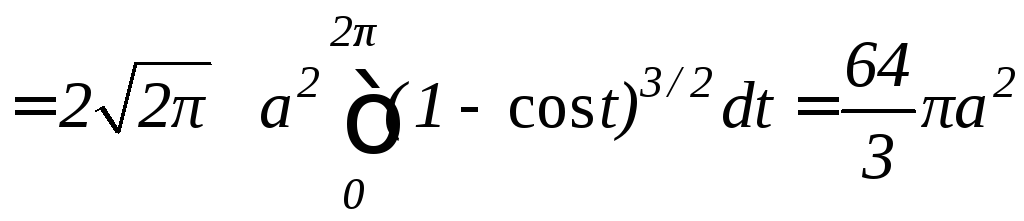г) Поскольку ,,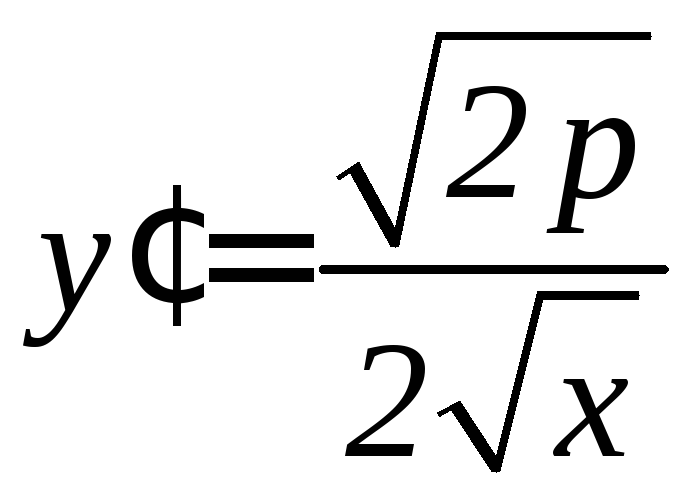, 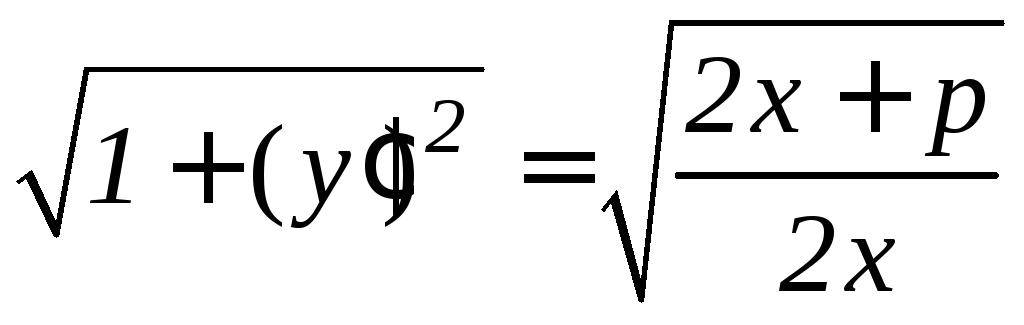то по формуле (9.14) получим

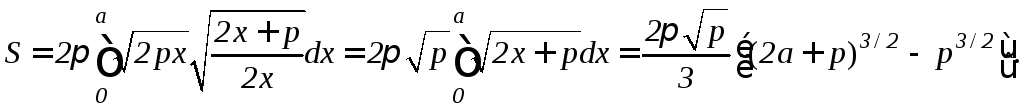
д) Пусть дуга окружности с центром в начале координат и радиусом R вращается вокруг оси Ox. Из уравнения окружности x²+y²=R² имеем y²=R²–x², yy= –x, значит

.

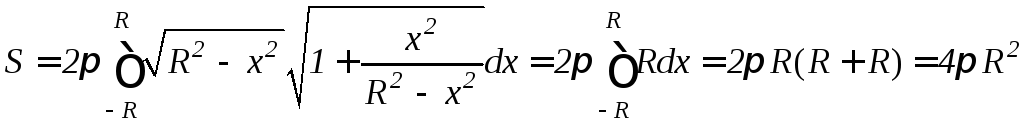Таким образом, площадь сферы S=4R².

9.11. Объем тела вращения

Если площадь сечения тела плоскостью, перпендикулярной осиOx, является непрерывной функцией на отрезке , то объем тела вычисляется по формуле:

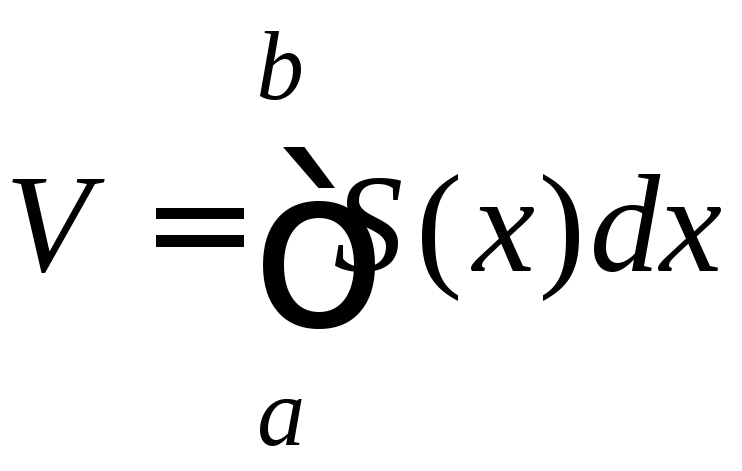. (9.16)

Выражение для функции получается достаточно просто в случае тел вращения. Если криволинейная трапеция, ограниченная кривой, вращается вокруг осиOx или оси Oy, то объемы тел вращения вычисляются по формулам:

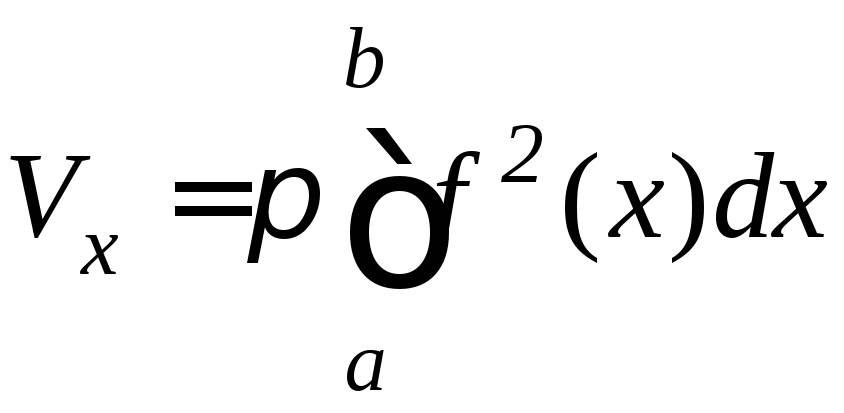
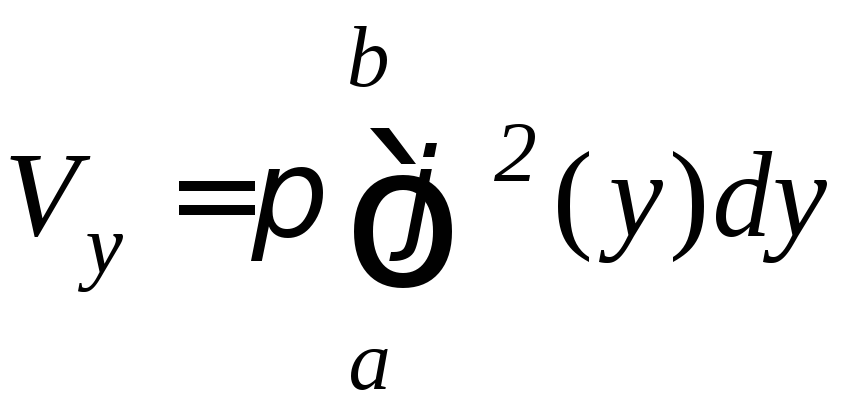или . (9.17)

Если криволинейный сектор, ограниченный кривой и лучами,, вращается вокруг полярной оси, то объем тела вращения равен:

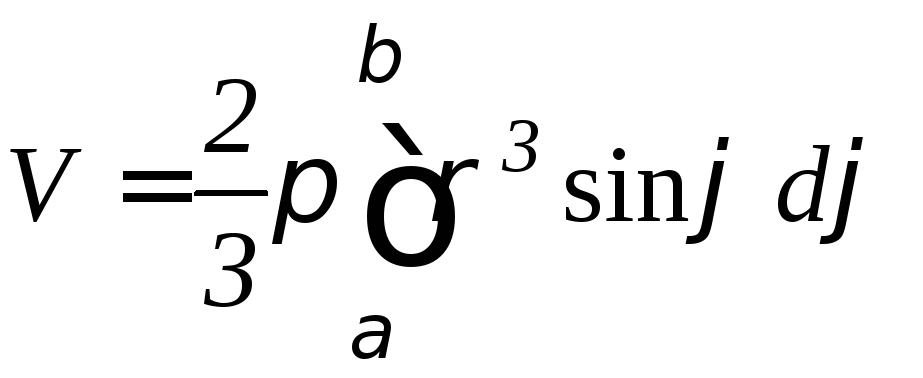. (9.18)

Отметим, что объемы тел значительно проще вычисляются при помощи кратных интегралов.

Пример 15. Найти объем тела, образованного вращением фигуры, ограниченной а) линиями 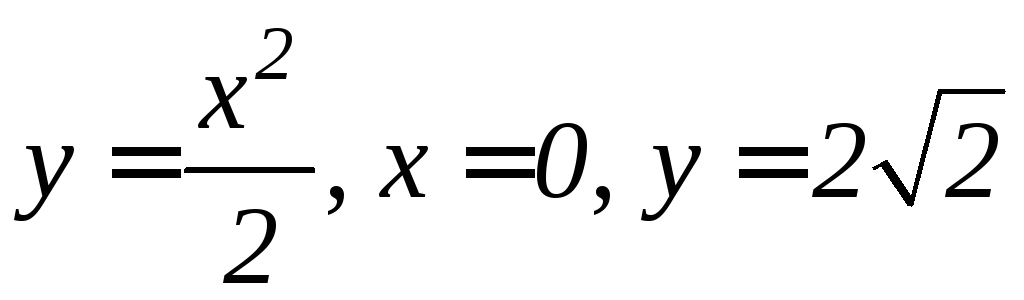вокруг осиOy;б)кардиоидой вокруг полярной оси.

Решение. а) Используя формулу (9.17),

найдем объем данного тела (рис. 9.17):

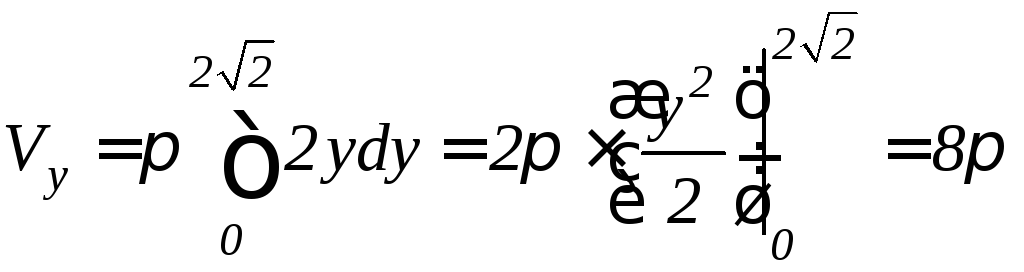(ед.³)

б) Используя формулу (9.18), найдем объем данного тела (рис. 9.18):

.

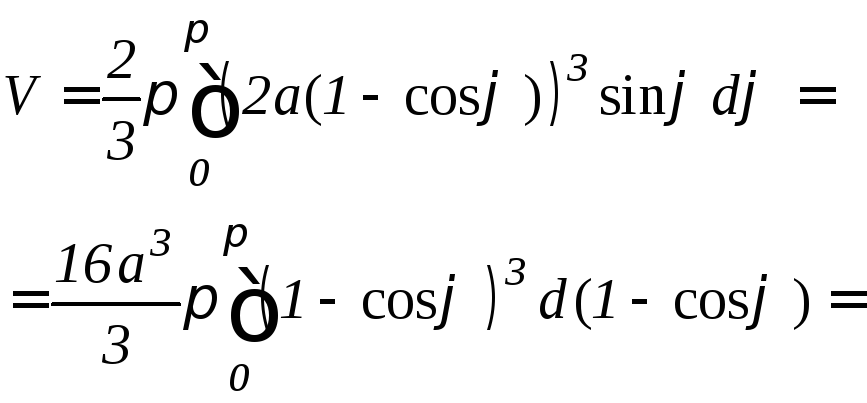
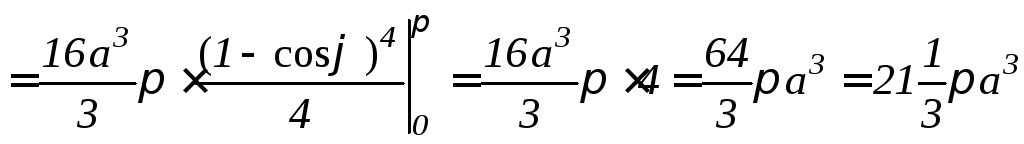9.12. Физические приложения. Вычисление работы с помощью определенного интеграла

Работа, совершаемая переменной силой F(x) при перемещении материальной точки вдоль оси Ox, равна

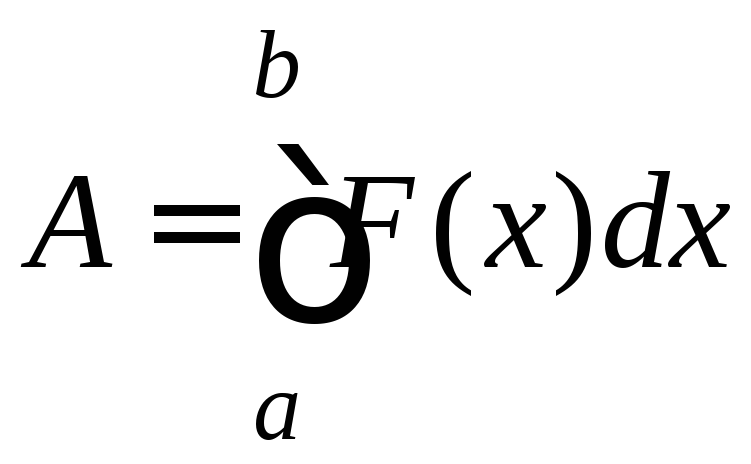. (9.19)

Рассмотрим пример нахождения работы, которую необходимо затратить, чтобы выкачать жидкость плотности  из резервуара, имеющего вид тела вращения, получающегося при вращении криволинейной трапеции вокруг оси Oy.

Пусть криволинейная трапеция в плоскости переменных ограничена линиямиx=f(y)>0, y=0, y=H, x=0. Элемент объема тела вращения равен ,

элемент веса равен .

Умножая элемент веса на (H–y_i) – высоту, на которую нужно поднять соответствующий вес при выкачивании жидкости – получим элемент работы:

.

Тогда работа по выкачиванию жидкости равна определенному интегралу по отрезку [0;H] :

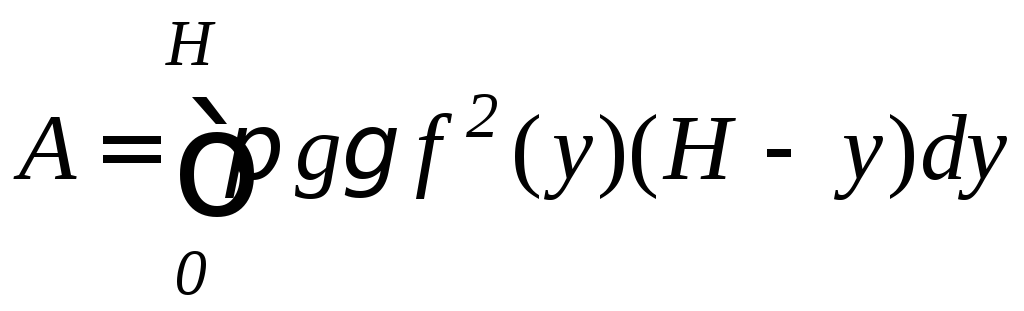. (9.20)

Пример 16. Вычислить работу, которую необходимо затратить, чтобы выкачать жидкость плотности  из резервуара, имеющего форму:

а) конуса вращения с вершиной, обращенной вниз и совпадающей с началом координат, высота которого H, а радиус основания R;

б) полусферы, обращенной выпуклостью вниз, радиус основания которой равен R;

в) цилиндра высоты H и радиуса основания R.

Решение. а) Данный конус получается в результате вращения прямой вокруг осиOy (см. рис. 9.19). По формуле (9.20) находим

.

б) Данная полусфера получается в результате вращения нижней четверти окружности вокруг осиOy (см. рис. 9.20). По формуле (9.20) находим

.

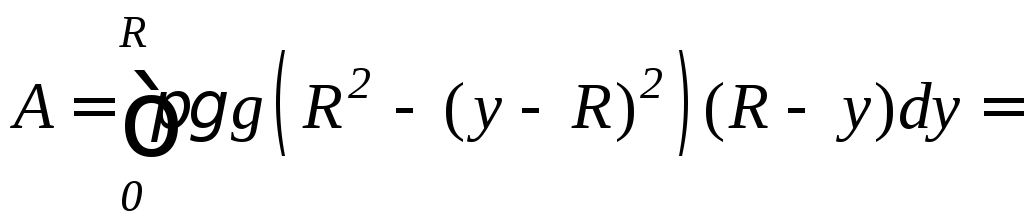
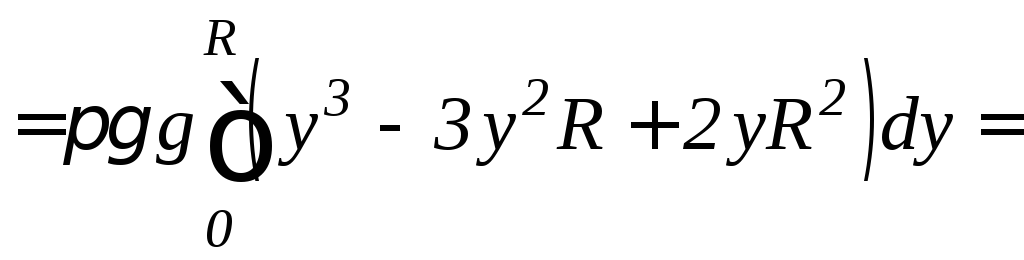
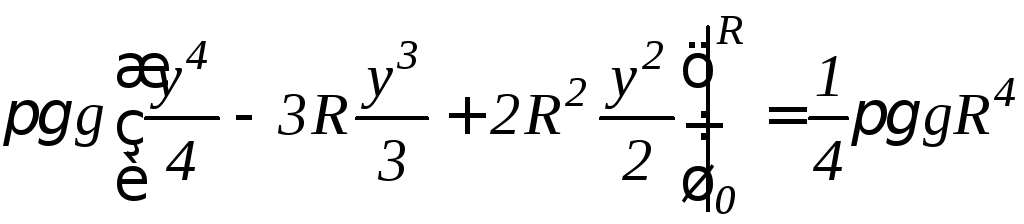в) Данный цилиндр получается в результате вращения отрезка прямой ,0yH вокруг оси Oy. Тогда

.

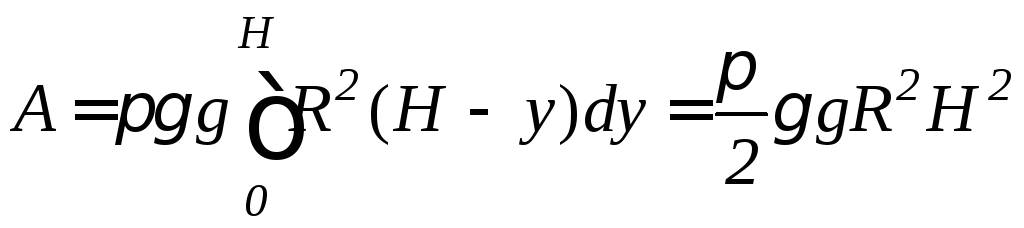9. 13. Вычисление координат центра тяжести, статических моментов и моментов инерции плоской кривой

Пусть дуга кривой задана уравнением , и имеет плотность. Тогдастатические моменты этой дуги относительно координатных осей Ox и Oy равны:

Рис. 9.20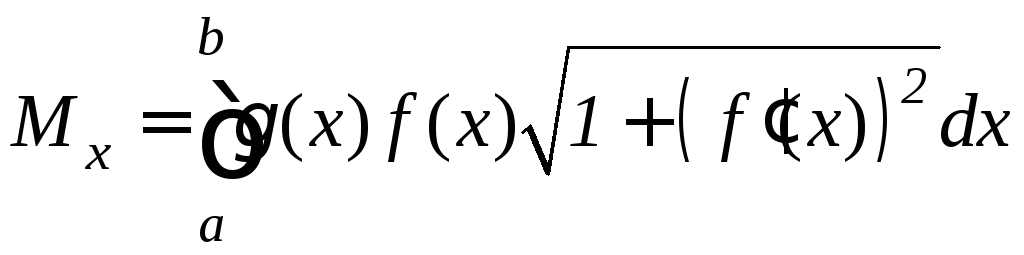

, (9.21)

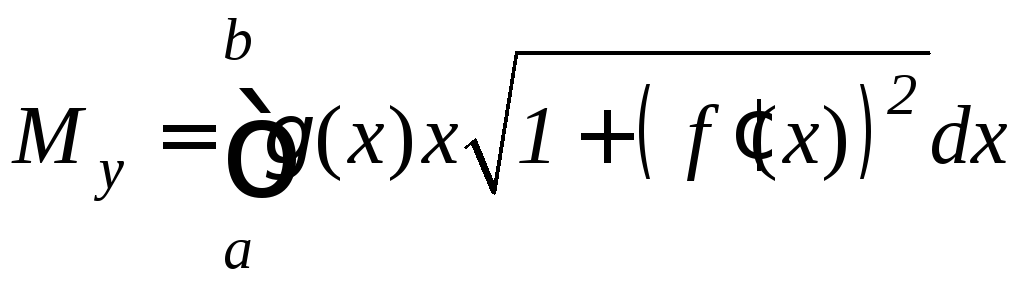. (9.22)

Моменты инерции дуги этой кривой относительно координатных осей Ox и Oy равны:

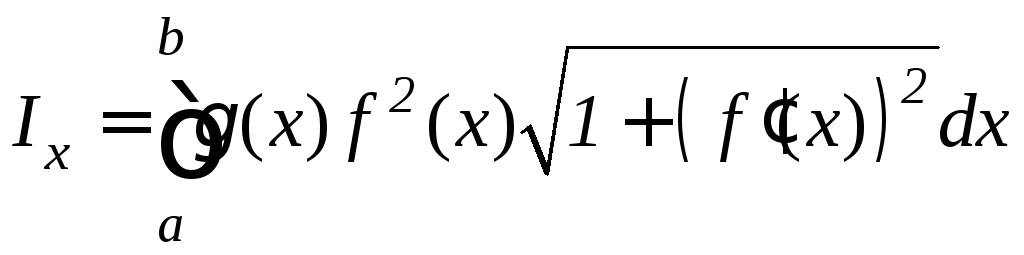, (9.23)

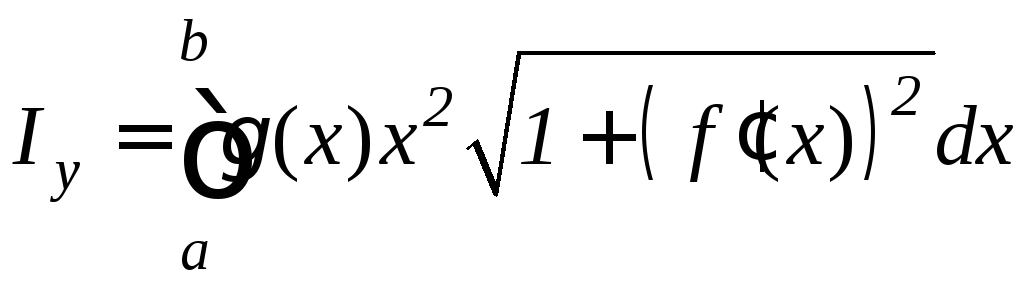. (9.24)

Координаты центра тяжестидуги этой кривой вычисляются по формулам:

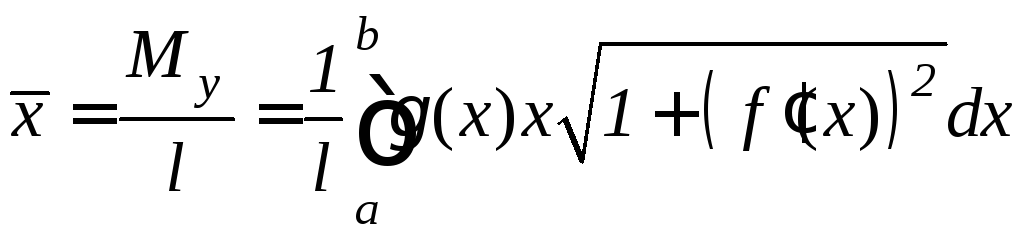, (9.25)

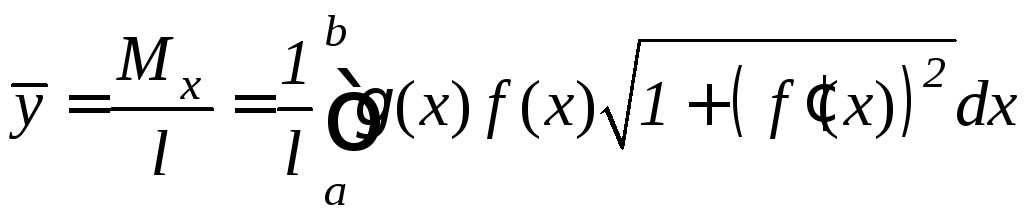, (9.26)

где l – масса дуги, определяемая по формуле:

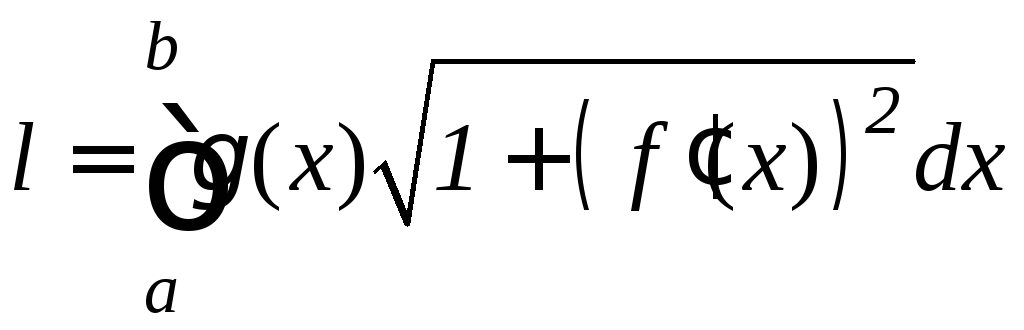. (9.27)

Пример 17. Найти координаты центра тяжести дуги окружности (рис. 9.21), при условии.

Решение. Длина дуги равна . Найдем массу этой дуги:. Используя формулу 9.21, найдем статический момент:

.

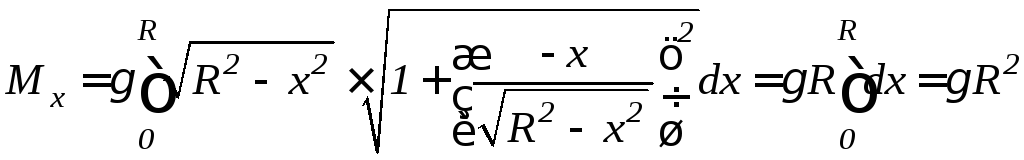Тогда 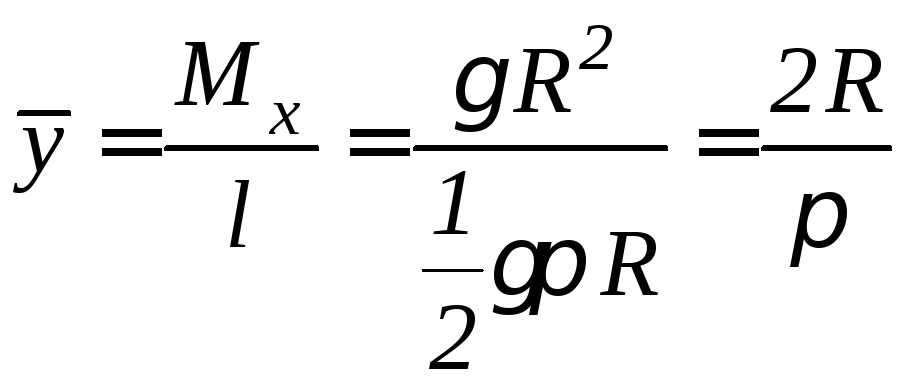. Учитывая симметричность дуги относительно биссектрисы координатного угла, получим. Центр тяжести имеет координаты.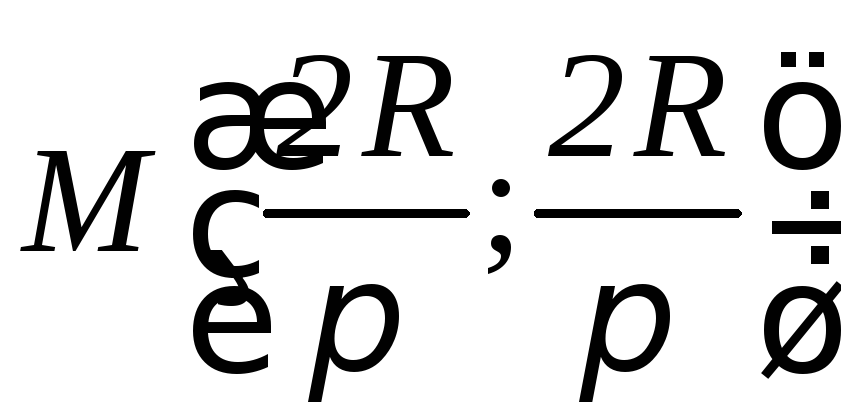

9. 14. Вычисление координат центра тяжести, статических моментов и моментов инерции плоской фигуры

Пусть плоская фигура ограничена кривой и прямыми, и имеет плотность. Тогдастатические моменты этой фигуры относительно координатных осей Ox и Oy равны:

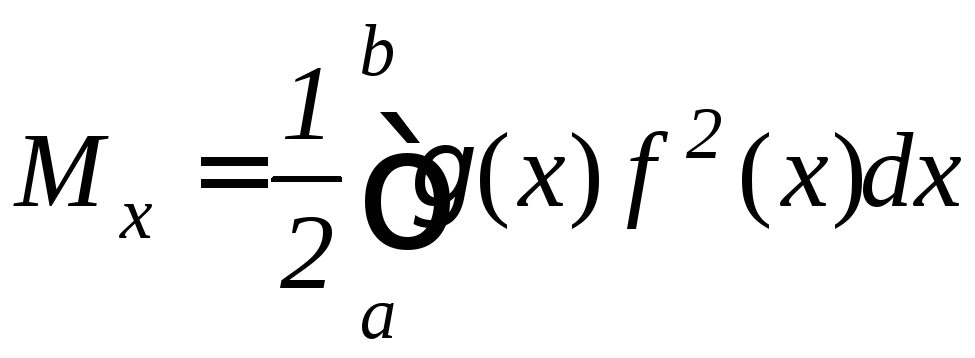, (9.28)

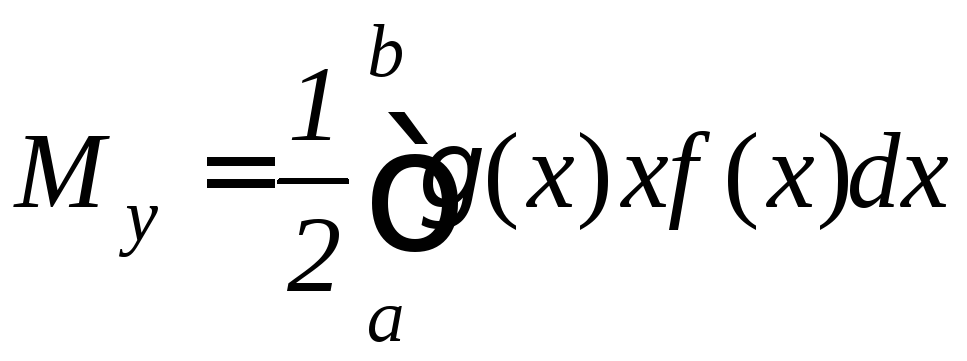. (9.29)

Моменты инерции этой фигуры относительно координатных осей Ox и Oy равны:

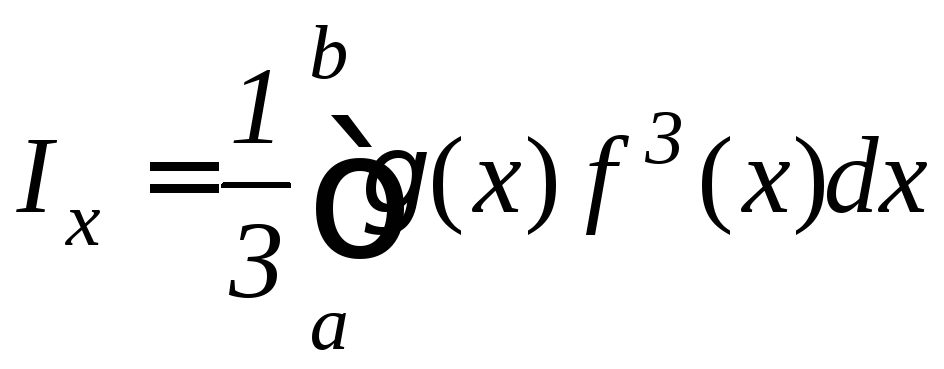, (9.30)

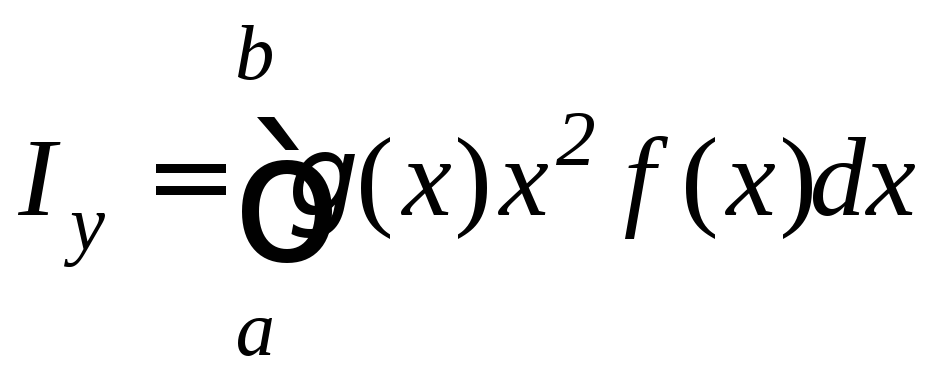. (9.31)

Координаты центра тяжести плоской фигуры вычисляются по формулам:

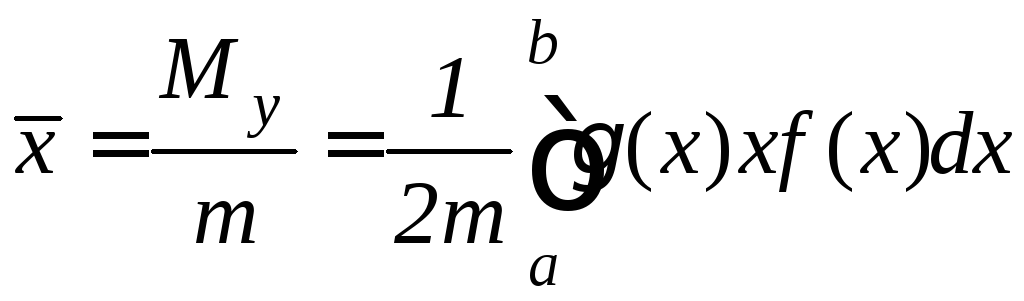, (9.32)

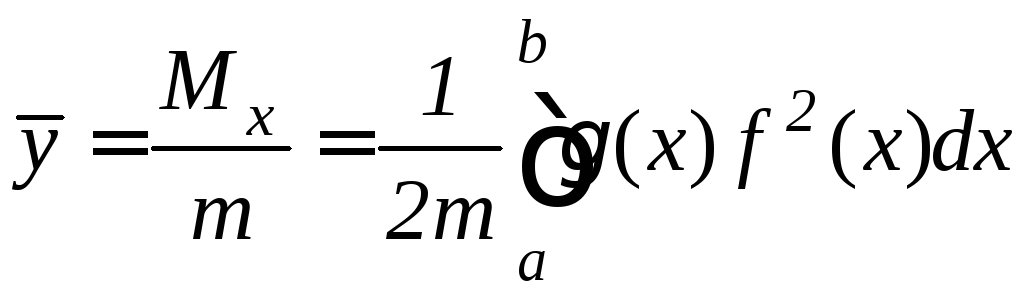, (9.33)

где m – масса фигуры, определяемая по формуле:

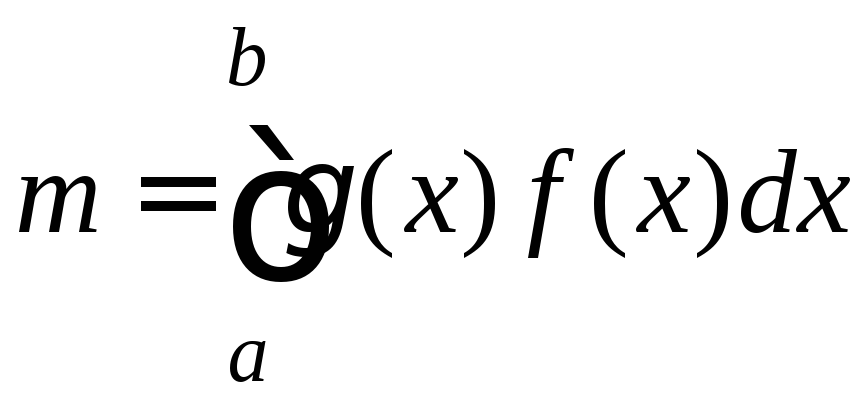. (9.34)

Пример 18. Найти координаты центра тяжести полукруга (рис. 9.22), при условии.

Решение. Площадь полукруга равна . Найдем массу этой фигуры:

.

Так как фигура симметрична относительно оси Oy, то . Используя формулу 9.28, найдем:

.

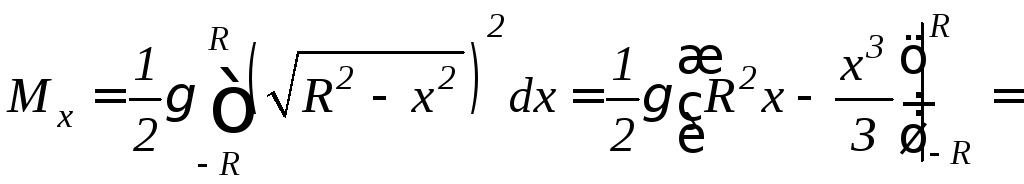
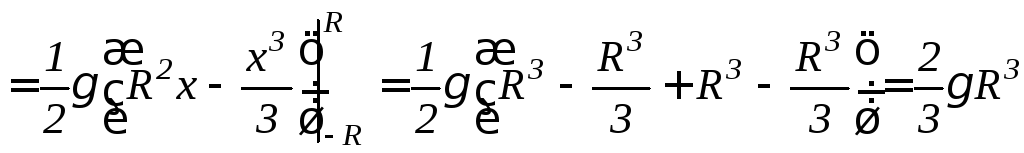По формуле 9.33, получаем:

.

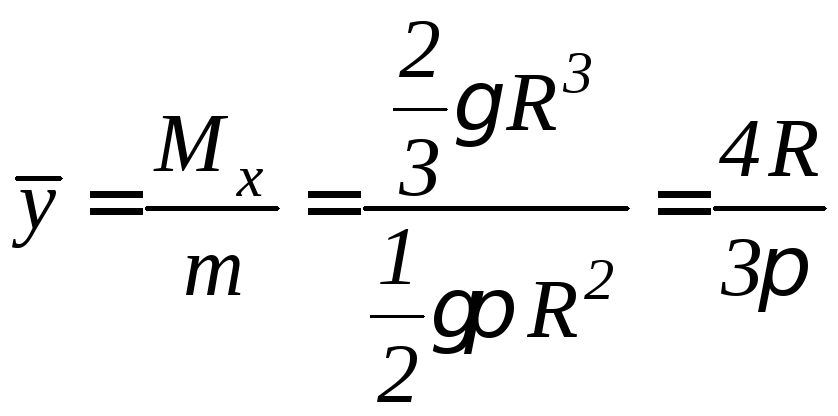Центр тяжести имеет координаты .
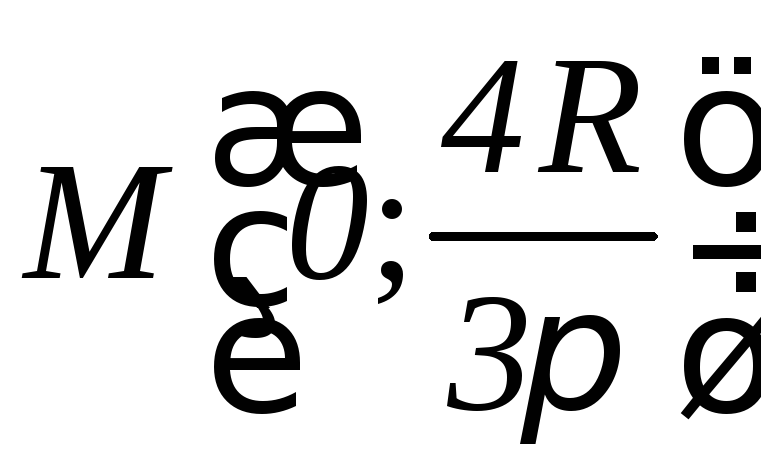