9.7. Параметрические функции

Пусть верхняя граница криволинейной трапеции задана параметрическими уравнениями: x=x(t), y=y(t), t₁ t t₂, причем x(t₁)=a, x(t₂)=b. Поскольку площадь криволинейной трапеции задается формулой S=(еслиy(x)0 на отрезке [a,b]), то, производя замену переменной, получим формулу для вычисления площади криволинейной трапеции, ограниченной кривой, заданной параметрически:

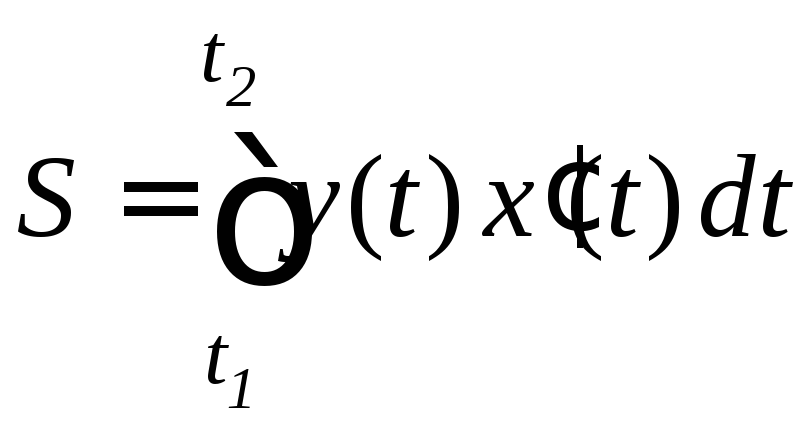(9.9)

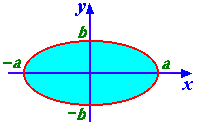
Пример 8. Вычислить площадь фигуры, ограниченной эллипсом ( рис. 9.9):

Рис. 9.9

.

Решение. Вычислим площадь верхней половины эллипса, а затем результат удвоим. Здесь x меняется от –a до a, следовательно, t должно изменяться от  до 0. Таким образом,

.

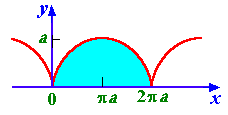
Пример 9. Вычислить площадь фигуры, ограниченной осью Oy и одной аркой циклоиды (см. рис. 9.10):

Рис. 9.10

Решение. Для получения одной арки циклоиды, достаточно чтобы t изменялось от 0 до 2. Тогда по формуле (9.9) получим

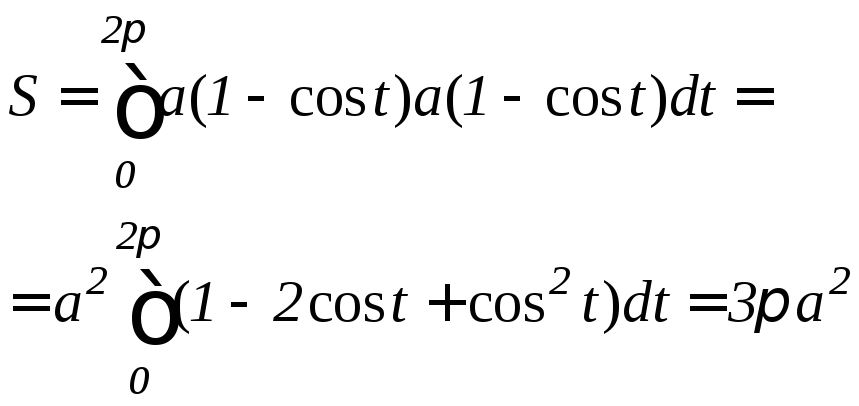
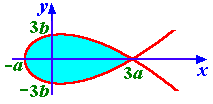
Пример 10. Вычислить площадь петли кривой (см. рис. 9.11):

Рис. 9.11

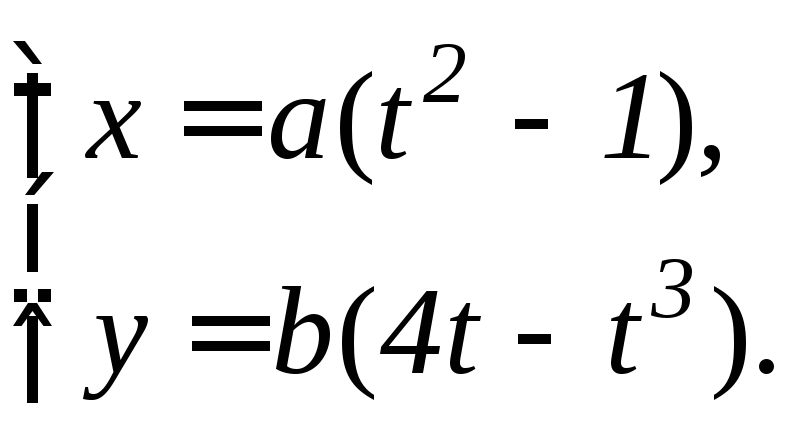
Решение. Кривая пересекается с осью Ox в двух точках: x₁= –a и x₂=3a при t₁=0 и t_2,3=2. Площадь петли находим как удвоенную площадь верхней ее половины:

.

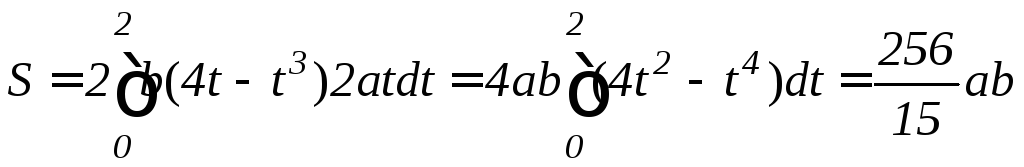9.8. Полярная система координат

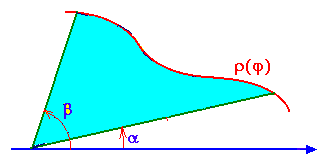
Пусть кривая задана в полярных координатах уравнением: =(), , причем функция () непрерывна и неотрицательна на отрезке []. Плоскую фигуру, ограниченную кривой () и двумя лучами, составляющими с полярной осью углы  и , будем называть криволинейным сектором (рис.9.12).

Рис. 9.12

Площадь криволинейного сектора вычисляется по формуле:

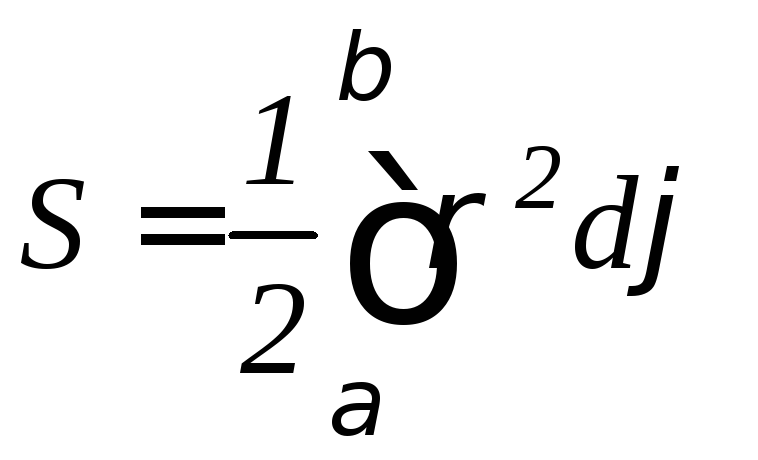. (9.10)

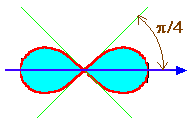
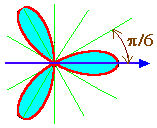
Пример 11. Вычислить площадь ограниченной: а) лемнискатой Бернулли ²=a²cos2 ; б) трехлепестковой розой =acos3.

Решение. а) Поскольку ²0, то cos20. Отсюда получаем

,

Рис. 9.13

где kZ. Таким образом, данная кривая расположена в двух секторах (см. рис. 9.13). Для нахождения искомой площади достаточно вычислить четверть площади, а затем умножить ее на 4. Воспользуемся формулой 9.10 :

.

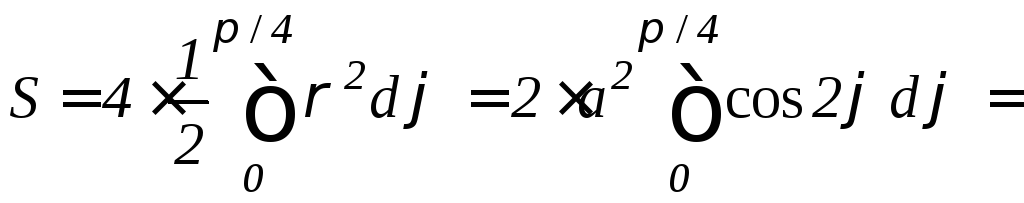
б) Поскольку 0, то cos30. Тогда получаем:

,

Рис. 9.14

где kZ. Таким образом, данная кривая будет расположена в трех секторах (см. рис. 9.14). Для нахождения искомой площади достаточно вычислить площадь половины одного "лепестка" и умножить ее на 6:

.

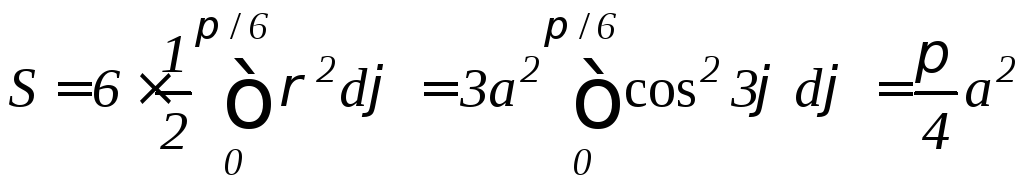9.9. Вычисление длины дуги плоской кривой

Если кривая на отрезке [a; b] – гладкая (т.е. производная – непрерывна), то длина соответствующей дуги этой кривой находится по формуле:

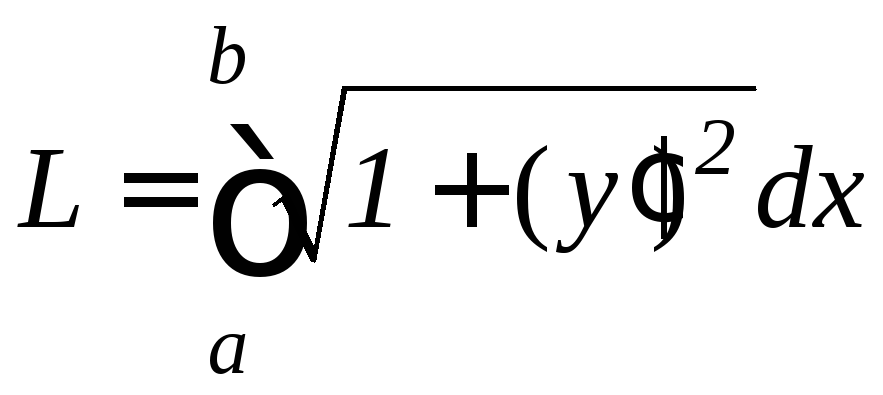. (9.11)

При параметрическом задании кривой (здесь– непрерывно дифференцируемые функции) длина дуги кривой, соответствующая монотонному изменению параметраt от t₁ до t₂, вычисляется по формуле:

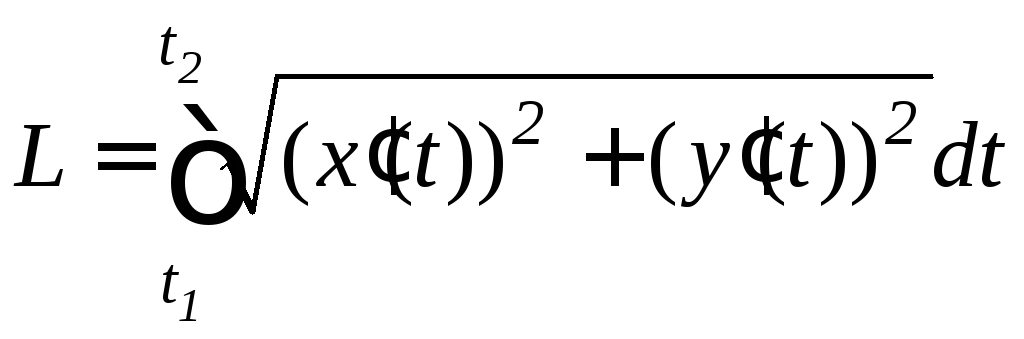. (9.12)

Если гладкая кривая задана в полярных координатах уравнением ,, то длина дуги равна:

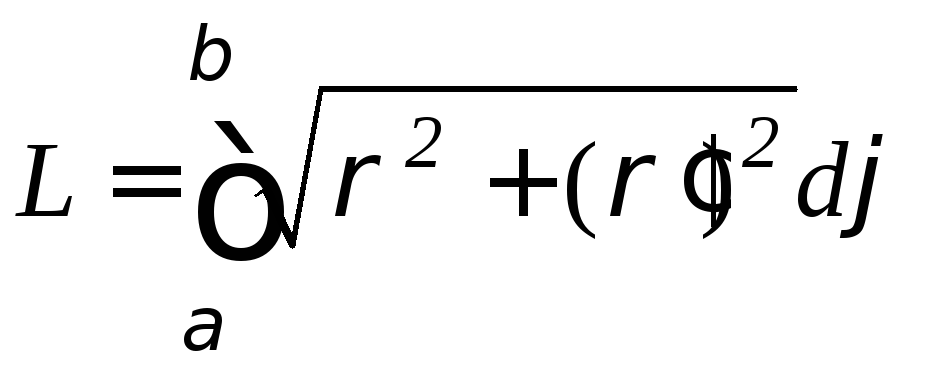
. (9.13)

Пример 13. Найти длину кардиоиды (рис. 9.15).

Решение. Найдем производную :

.Подставляя в формулу (9.13) получим:

.
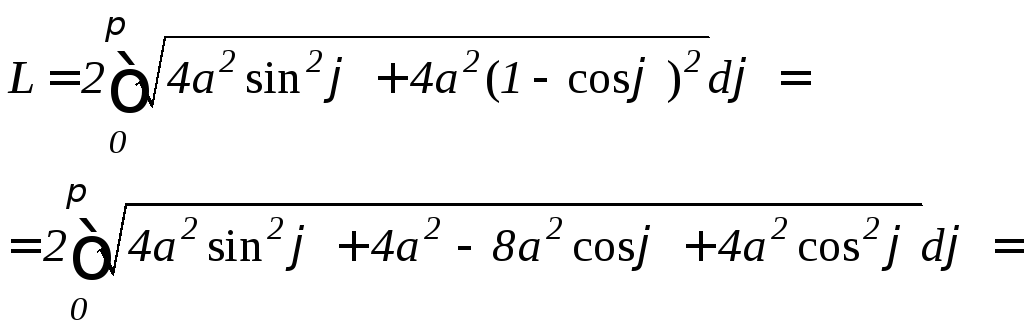
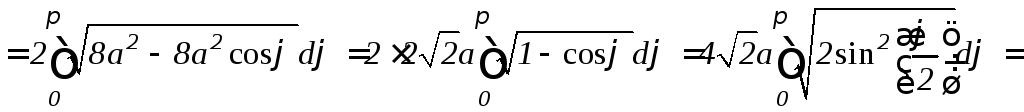
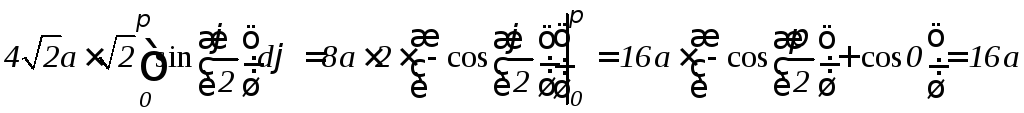