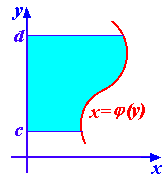
9.6. Вычисление площадей плоских фигур

Рис. 9.1.

Напомним геометрический смысл определенного интеграла

.

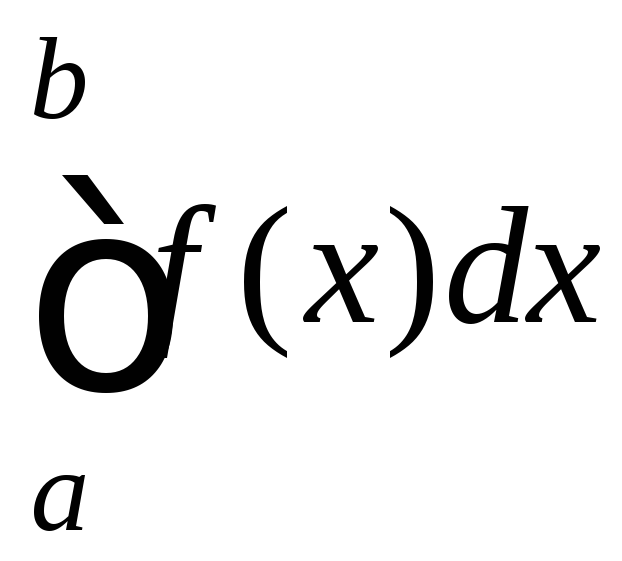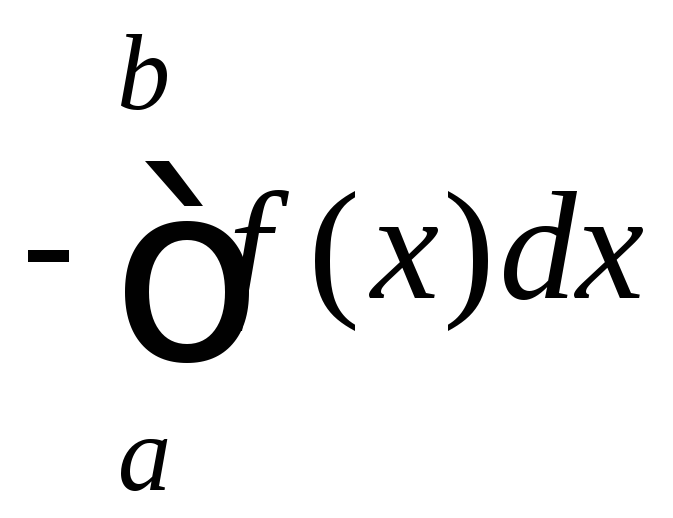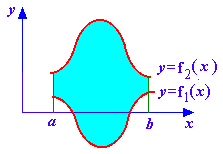
Если f(x)0, то определенный интеграл есть площадь криволинейной трапеции, ограниченной графиком функции f(x), прямыми x=a и x=b, а также осью Ox. Если же функция f(x) 0, то определенный интеграл будет меньше нуля. Знак минус означает, что криволинейная трапеция расположена ниже оси Ox и ее площадь будет равна S=. Может оказаться, что функцияf(x) на отрезке интегрирования несколько раз меняет знак. В этом случае интеграл нужно разбить на сумму интегралов по участкам, на которых подынтегральная функция имеет постоянный знак. Например, площадь фигуры на рис. 9.1 будет иметь вид

S=.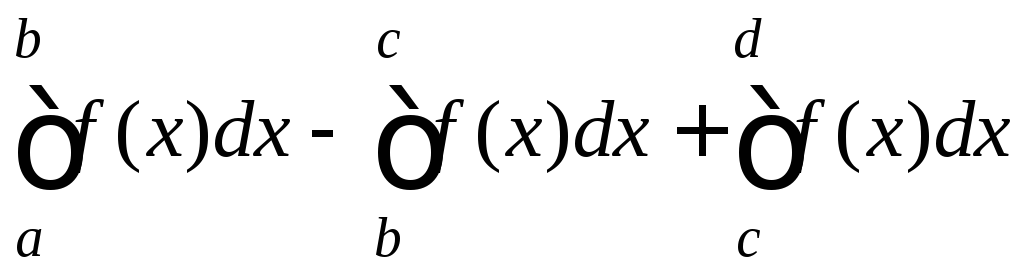

Пример 4. Вычислить площадь фигур, ограниченных линиями:

а) y=sinx, y=0, 0x2; б) y=x–x², y=0, 0x2.

Рис. 9.2

Решение. а) Сделаем чертеж (см.
рис. 9.2). Так как при0x sinx0 и при x2 sinx0, то

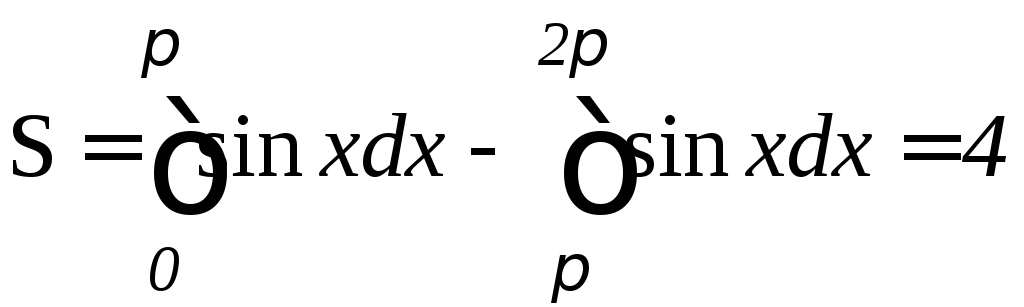(кв. ед.)

Рис. 9.3

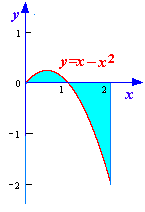
б) Сделаем чертеж (см. рис. 9.3). Найдем точки пересечения параболы с осью Ox:

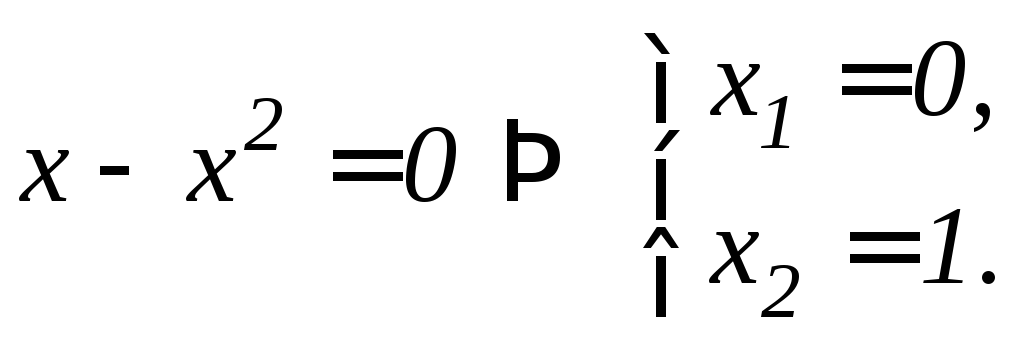
Из рисунка видно, что

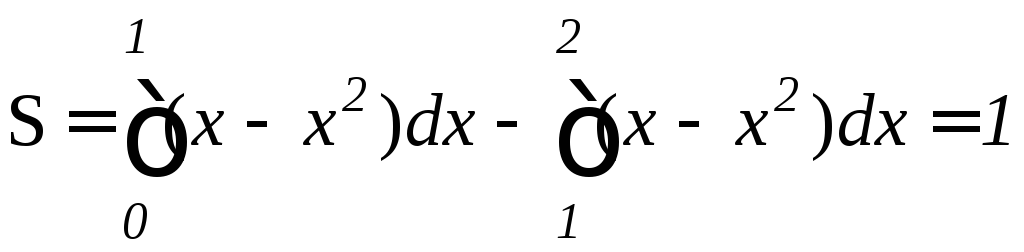(кв. ед.)

Рис. 9.4

Пусть плоская фигура на отрезке [a,b] ограничена графиками двух функций y=f₁(x) и y=f₂(x), причем f₂(x)f₁(x) (см. рис. 9.4). Тогда искомая площадь вычисляется по формуле:

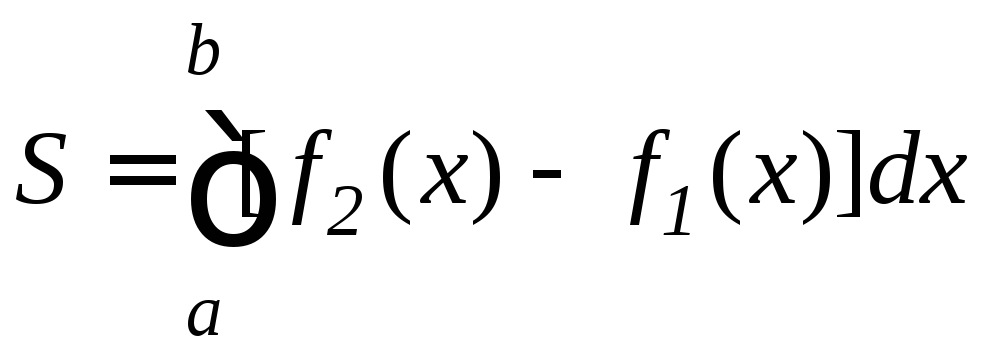. (9.7)

Рис. 9.5

Пример 5. Вычислить площадь фигуры, ограниченной линиями: y=x–x², y=–x.

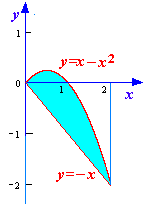
Решение. Сделаем чертеж (см. рис. 9.5). Найдем точки пересечения параболы и прямой:

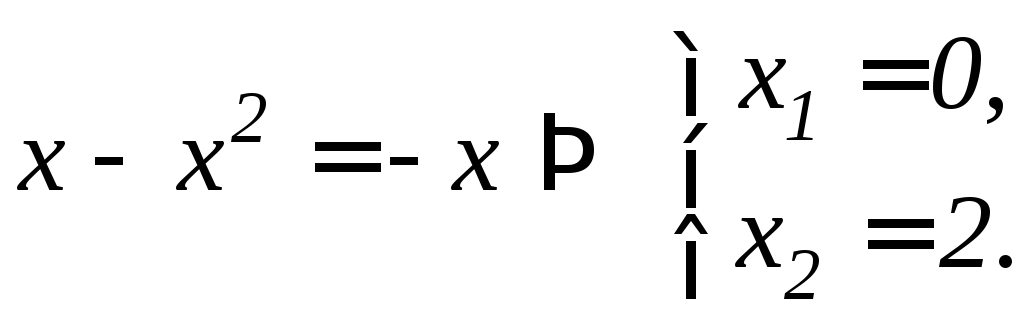
Поскольку на отрезке [0;2] x–x²  –x, то площадь заданной фигуры будет равна

.

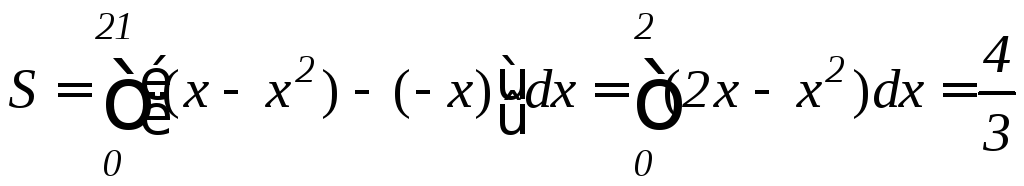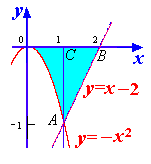
Пример 6. Вычислить площадь фигуры, ограниченной линиями: y=–x², y=x–2, y=0.

Рис. 9.6

Решение. Из чертежа (см. рис. 9.6) видно, что искомую площадь S фигуры OAB можно рассматривать как площадь над кривой OAB на отрезке [0;2]. Однако указанная кривая (ломаная) не задается одним уравнением. Поэтому для нахождения искомой площади разобьем фигуру OAB на две части: OAC и ACB. Найдем абсциссу точки A:

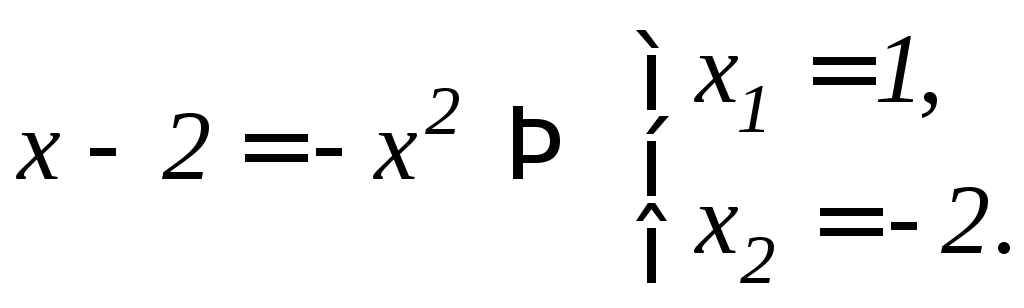
Таким образом, точка A имеет координаты (1;–1). После этого находим площадь заданной фигуры:

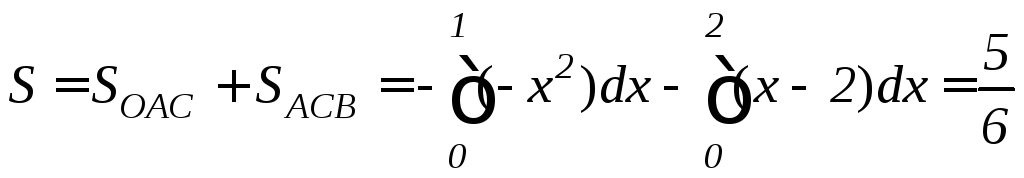(кв.ед.).

Рис. 9.7

Заметим, что криволинейная трапеция может образовываться графиком функции также и с осью Oy (см. рис. 9.7). Тогда площадь такой криволинейной трапеции можно записать в виде

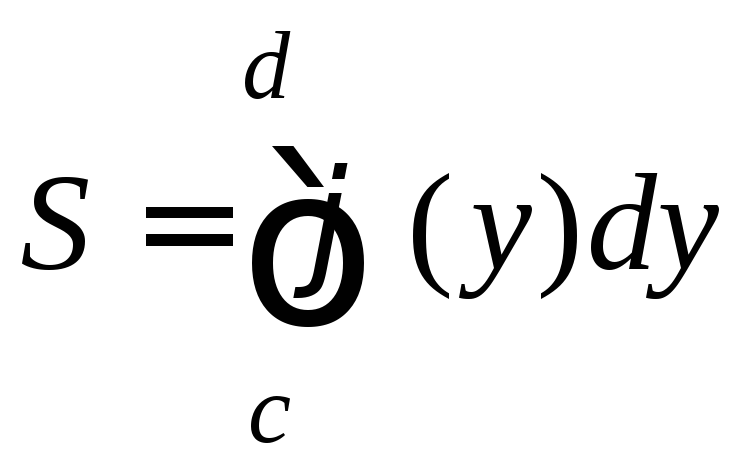. (9.8)

Такой случай следует иметь ввиду, поскольку это может сильно сократить вычисления.

В частности, последний пример можно решить относительно оси Oy (переменной y). В этом случае фигура OAB будет ограничена снизу кривой , а сверху – прямойx₂=y+2. В результате, площадь фигуры будет вычисляться следующим образом:

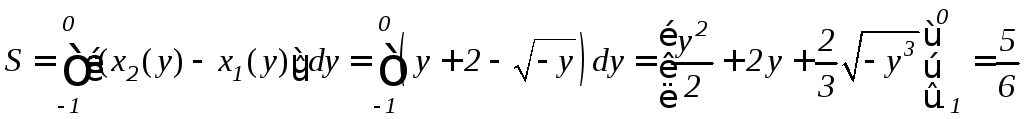(кв.ед.)

Рис. 9.8

Пример 7. Вычислить площадь фигуры, ограниченной параболами:

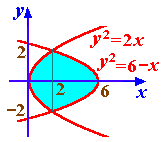
y²=2x и y²=6–x (см. рис. 9.8).

Решение. Будем искать площадь данной фигуры относительно оси Oy. Ординаты точек пересечения линий равны y₁=–2 и y₂=2. Следовательно,

(кв. ед.)