
- •1. Безнапорное движение жидкости. Особенности гидравлики безнапорных потоков.
- •9.1. Определения и расчетные зависимости
- •2. Равномерное движение в открытых руслах. Основные задачи при расчете равномерного движения.
- •3. Вывод дифференциального уравнения неравномерного движения в виде
- •4. Вывод дифференциального уравнения неравномерного движения для призматического русла из выражения (10.4)
- •5. Удельная энергия сечения и ее график. Критическая и нормальная глубины, критический уклон, их определение.
- •7. Виды кривых свободной поверхности при положительном уклоне дна.
- •8. Характер изменения удельной энергии и глубины потока при подходе к h0, hкр и h→∞. Определение критической глубины для прямоугольного русла.
- •11. Гидравлический прыжок в прямоугольном русле. Определение потерь энергии в прыжке. Основные определения и классификация
- •12. Вывод формулы гидравлического прыжка. Прыжковая функция. Графоаналичтический метод определения места расположения гидравлического прыжка.
- •13. Вывод формулы сопряженных глубин для прыжка в прямоугольном русле. Определение потерь энергии при возникновении прыжка.
- •14. Построение кривых свободной поверхности в естественных руслах. Особенности построения кривых свободной поверхности в естественных руслах
- •15. Типы водосливов. Водослив с тонкой стенкой. Водосливы практического профиля. Водослив с широким порогом. Постулаты Баланже и Бахметьева.
- •12.3. Водосливы с тонкой стенкой
- •12.4. Водосливы практического профиля
- •12.5. Водосливы с широким порогом
- •16. Определение глубины водобойного колодца и высоты водобойной стенки.
- •17. Виды, назначение и принцип действия гидравлических машин. Их основные параметры.
- •15.1. Насосы
- •15.1.1. Объемные насосы
- •15.1.2. Лопастные насосы
- •15.2. Гидротурбины
- •15.2.1. Активные турбины
- •15.2.2. Реактивные турбины
- •15.3. Гидропередача
- •15.3.1. Гидродинамическая передача
- •15.3.2. Объемная гидропередача
- •18. Устройство и принцип действия центробежных насосов. Баланс энергии и коэффициент полезного действия центробежных насосов. Характеристики работы насоса
- •19. Вывод основного уравнения для теоретического напора центробежного насоса.
- •20. Форма лопастей и их влияние на теоретический напор центробежного насоса.
- •21 Теоретическая и действительная характеристика центробежного насоса
- •22 Работа центробежного насоса на трубопровод
- •24 Последовательное и параллельное соединение центробежных насосов
8. Характер изменения удельной энергии и глубины потока при подходе к h0, hкр и h→∞. Определение критической глубины для прямоугольного русла.
При неравномерном движении воды кривые свободной поверхности могут приближаться к линиям нормальной (при I0 > 0) или критической глубины, которые для цилиндрических и призматических русел остаются постоянными на всем их протяжении. Рассмотрим особенности изменения глубин в этих случаях.
Если
глубина неравномерного движения
стремится к нормальной глубине
 ,
то модуль расхода стремится к нормальному
модулю
,
то модуль расхода стремится к нормальному
модулю .
Тогда из уравнения (10.8) следует, что
.
Тогда из уравнения (10.8) следует, что .
Это значит, что глубина стремится не
изменяться вдоль потока, стать постоянной,
т. е. кривая свободной поверхности
асимптотически приближается к линии
нормальных глубин (рис. 10.11.а).
.
Это значит, что глубина стремится не
изменяться вдоль потока, стать постоянной,
т. е. кривая свободной поверхности
асимптотически приближается к линии
нормальных глубин (рис. 10.11.а).
Пусть
глубина неравномерного движения
приближается к линии критических глубин
 .
Из определения критической глубины
это означает, что удельная энергия
сечения стремится к минимуму и
.
Из определения критической глубины
это означает, что удельная энергия
сечения стремится к минимуму и .
Тогда из уравнения (10.6) следует, что
.
Тогда из уравнения (10.6) следует, что
 ,
,
и
знаменатель выражения (10.8) стремится
к нулю, а, следовательно,
 .
Это означает, что кривая свободной
поверхности стремится подойти к линии
критических глубин перпендикулярно.
.
Это означает, что кривая свободной
поверхности стремится подойти к линии
критических глубин перпендикулярно.

Рис. 10.11
Результаты исследований на натурных потоках показывают, что на самом деле в этом случае кривая свободной поверхности подходит к линии критических глубин не перпендикулярно, а под достаточно крутым углом (рис. 10.11.б). Это обстоятельство объясняется тем, что в области глубин, близких к критической, существенна кривизна потока, и не выполняется условие плавной изменяемости движения. В этом случае уравнение Бернулли и вытекающее из него уравнение (10.8) не достаточно соответствуют условиям движения воды.
При
больших глубинах, т. е. при
 ,
будет
,
будет и
и (см. рис. 10.8). Тогда из уравнения (10.8)
имеем
(см. рис. 10.8). Тогда из уравнения (10.8)
имеем
 .
.
Так
как и уклон дна равен
 ,
то в этом случае свободная поверхность
стремится стать горизонтальной. Обычно
такая ситуация наблюдается в
водохранилищах, прудах и других водоемах
с большими глубинами.
,
то в этом случае свободная поверхность
стремится стать горизонтальной. Обычно
такая ситуация наблюдается в
водохранилищах, прудах и других водоемах
с большими глубинами.
Таким образом, при неравномерном движении кривые свободной поверхности подходят асимптотически к линии нормальных глубин, под крутым углом к линии критических глубин и при больших глубинах линии свободной поверхности стремятся стать горизонтальными.
При
этих общих особенностях в зависимости
от уклона дна
 и соотношения глубины неравномерного
движенияh,
нормальной глубины
и соотношения глубины неравномерного
движенияh,
нормальной глубины
 и критической глубины
и критической глубины возникают различные формы кривых
свободной поверхности.
возникают различные формы кривых
свободной поверхности.
9 и 10. Интегрирование уравнения неравномерного движения для призматического русла при положительном, горизонтальном и отрицательном уклонах дна.
Интегрирование дифференциальных уравнений
неравномерного движения по методу Б. А. Бахметьева
Для построения кривой свободной поверхности проинтегрируем уравнение (10.8):
 .
.
Преобразуем
знаменатель этого уравнения. Так как
 ,
то получим
,
то получим
 .
.
Используя соотношения
 ,
,
будем иметь
 .
.
Обозначим
|
|
|
(10.14) |
и знаменатель уравнения (10.8) примет вид
 .
.
Подставляя его в уравнение, получим
|
|
|
(10.15) |
Используем показательную зависимость Б. А. Бахметьева в виде (10.12)
 .
.
Введем обозначение
 ,
,
величина
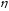 называется относительной глубиной.
называется относительной глубиной.
Из этого соотношения получим
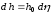 .
.
Тогда уравнение (10.15) запишется в виде
![]() .
.
Проинтегрируем полученное уравнение вдоль потока от сечения 1–1 до сечения 2–2, расположенного на некотором расстоянии от сечения 1–1 вниз по потоку. Будем отмечать гидравлические элементы сечения 1–1 индексом 1, элементы сечения 2–2 – индексом 2. В результате получим
 .
.
Допустим,
что величина j
мало меняется с изменением глубины
потока, специальные расчеты подтверждают
это. Тогда скобку
 можно вынести за знак интеграла, приняв
среднее значение величиныj
на расчетном участке. Это среднее
значение величины jср
можно вычислить по формуле
можно вынести за знак интеграла, приняв
среднее значение величиныj
на расчетном участке. Это среднее
значение величины jср
можно вычислить по формуле
![]() ,
,
где j1 и j2 рассчитываются по формуле (10.14) соответственно для глубин h1 и h2.
Величину jср можно также рассчитать по формуле (10.14)
 ,
,
где
величины
 вычисляются для глубины
вычисляются для глубины
 .
.
Тогда интегрируемое уравнение можно записать как
 .
.
Так
как мы считаем для данного русла величину
гидравлического показателя x
постоянной, то подынтегральная функция
этого уравнения зависит только от
 .
Введем обозначение
.
Введем обозначение
 ,
,
где С – произвольная константа интегрирования.
Тогда окончательно получим уравнение кривой свободной поверхности в виде
|
|
|
(10.16) |
Уравнение (10.16) называется уравнением Бахметьева для случая I0 > 0.
Функции
 для различных значений
для различных значений иx
вычислены и занесены в таблицы. Установив
величину гидравлического показателя
x
для
исследуемого русла по таким таблицам
можно определить значения функций
иx
вычислены и занесены в таблицы. Установив
величину гидравлического показателя
x
для
исследуемого русла по таким таблицам
можно определить значения функций
 и
и для предварительно вычисленных
для предварительно вычисленных и
и .
.
Пользуясь уравнением (10.16) можно решать следующие практические задачи:
задана глубина h1 (или h2), требуется определить глубину h2 (или h1) в сечении потока, расположенном на расстоянии
 от первого сечения;
от первого сечения;заданы две глубины в разных сечениях: h1 и h2, требуется определить расстояние
 между этими сечениями;
между этими сечениями;задана глубина h1 в некотором сечении, требуется построить кривую свободной поверхности.
Метод
Б. А. Бахметьева, использующий показательную
зависимость между глубинами и модулями
расхода потока, можно применять и для
расчета движения воды в русле с
горизонтальным уклоном ( )
и в русле с обратным уклоном (
)
и в русле с обратным уклоном ( ).
).
Для течения в горизонтальном русле показательная зависимость записывается в виде
|
|
|
(10.17) |
в котором действительные элементы потока h и K относятся к критическим элементам h к и K к.
Для русел с обратным уклоном показательную зависимость запишем так:
|
|
|
(10.18) |
Здесь
 – модуль расхода, отвечающий некоторой
воображаемой нормальной глубине
– модуль расхода, отвечающий некоторой
воображаемой нормальной глубине ,
которая получается, если представить,
что при заданном расходеQ
вода движется по
уклону,
т. е. в обратную сторону относительно
действительного течения, причем в русле
установился равномерный режим.
,
которая получается, если представить,
что при заданном расходеQ
вода движется по
уклону,
т. е. в обратную сторону относительно
действительного течения, причем в русле
установился равномерный режим.
Используя зависимости (10.17) или (10.18) и проведя преобразования, аналогичные вышеизложенным, получаем уравнения Б.А.Бахметьева для случаев горизонтального русла и русла с обратным уклоном.

 ,
, .
. .
. ,
, .
.