0

Федеральное агентство морского и речного

ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО

ОБРАЗОВАНИЯ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ

————————————————————————————————

Ястребов М.Ю.

МАТЕМАТИКА

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Санкт-Петербург

2007

УДК

ББК

Рецензент:

Кандидат физико-математических наук, доцент

Кузнецов В.О.

Ястребов М.Ю. Математика. Числовые и функциональные ряды. — Учебное пособие: СПб: СПГУВК, 2007 — 48 С.

Учебное пособие предназначено для студентов первого курса экономических и технических специальностей. Оно соответствует рабочей программе дисциплины «Математика» и может быть использовано как при подготовке к экзамену, так и для текущих учебных занятий.

УДК

ББК

© Санкт-Петербургский государственный

Университет водных коммуникаций, 2007

Введение

Понятие ряда связано с обобщением операции сложения на случай бесконечного числа слагаемых.

Математики прошлого спорили о том, чему равна бесконечная сумма

.

При одном способе расстановки скобок:

разумно считать, что эта сумма равна нулю. При другом способе:

разумным представляется, что эта сумма равна единице. Что же является верным?

С современной точки зрения правильным является не вопрос «чему равна эта сумма», а вопрос «как следует определить сумму бесконечного числа слагаемых». Затем, исходя из уже имеющегося определения суммы, следует выяснять, чему эта сумма равна в каждом отдельном случае.

Сумму бесконечного числа слагаемых называют рядом, а отдельные слагаемые — членами ряда. Важная теоретическая и прикладная роль рядов связана с тем, что они дают простой и наглядный способ представления функций и отдельных (прежде всего, иррациональных) чисел.

В школьной математике с суммой бесконечного числа слагаемых сталкиваются (правда, без точных формулировок) при изучении суммы бесконечно убывающей геометрической прогрессии, которая играет важную роль в теории рядов.

ГЛАВА 1. Числовые ряды

1.1. Сходимость числового ряда

Пусть задана числовая последовательность :

.

Определение. Числовым рядом называется выражение

(1)

Числа называются при этом членами ряда. Общий член последовательности, записанный как функция номера, называетсяобщим членом ряда.

Подчеркнем, что в данном определении, по существу, вводится пока только обозначение суммы бесконечного числа слагаемых. Что следует считать значением этой суммы — дело следующих определений.

Определение. –й частичной суммой ряда (1) называется сумма первыхчленов ряда:

.

Так,

;

;

…

;

. (2)

Частичные суммы образуют числовую последовательность; эта последовательность может иметь конечный или бесконечный предел, либо не иметь предела.

Определение. Если существует конечный предел последовательности частичных сумм:

,

то говорят, что ряд (1) сходится, а число — егосумма. Если предел бесконечен или не существует, то говорят, что ряд расходится.

Примеры. 1. Разделим отрезок , имеющий длину 1, пополам и в качествевозьмем длину левой части:.

Далее, оставшуюся правую часть разделим пополам и в качестве возьмем длину левой ее половины: и т.д. Продолжая процесс до бесконечности, получаем для длины отрезкапредставление в виде суммы бесконечного числа слагаемых, которые являются членами геометрической прогрессии с начальным членоми знаменателем:

(рис. 1). Здесь частичные суммы:

стремятся к длине исходного отрезка, то есть к :. Ряд сходится, и его сумма равна.

2. Рассмотрим ряд

у которого, очевидно, . Предел частичных сумм бесконечен; ряд расходится.

3. Рассмотрим ряд

.

Здесь последовательность частичных сумм

не имеет предела; ряд расходится.

Наряду с рядами вида , в которых нумерация слагаемых начинается с единицы, рассматривают также ряды, в которых нумерация начинается с произвольного целого числа:

После перенумерации членов по формуле такие ряды принимают вид (1), и для них сохраняются понятия сходимости и суммы ряда.

1.2. Необходимый признак сходимости ряда

Теорема. Если числовой ряд сходится, то предел его общего члена равен нулю:.

Доказательство. Пусть ряд сходится, и его сумма равна: . Тогда из равенства (2) следует:

.

Отсюда по свойствам предела:

. ■

Замечания. 1. Необходимый признак сходимости ряда не является достаточным: из стремления к нулю общего члена ряда не следует существование конечного предела последовательности частичных сумм. Так, для ряда с общим членомимеем:. В то же время последовательность частичных суммстремится к бесконечности. Действительно,

.

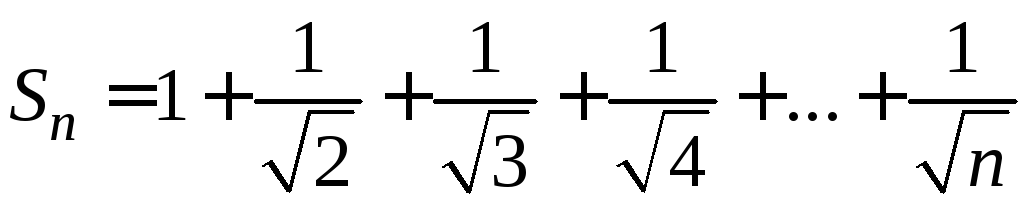Заменяя в сумме справа каждое из слагаемых наименьшим из них, получаем:

.

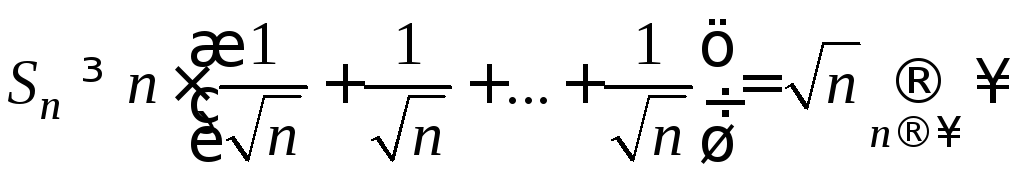2. Из теоремы следует, что если общий член ряда не стремится к нулю, то ряд заведомо расходится.