7. Виды кривых свободной поверхности при положительном уклоне дна.

Уклон дна меньше критического

В случае, когда уклон дна меньше критического , нормальная глубина будет больше критической –(рис. 10.12). Это означает, что линия нормальных глубинН–Н проходит выше линии критических глубин К–К. Неравномерное движение при этом может устанавливаться в трех зонах:

• зона a – при ;

• зона b – при ;

• зона c – при .

Рассмотрим особенности линий свободной поверхности в каждой из этих зон.

Рис. 10.12

Зона a

В этой зоне , а значит (см. рис. 10.5). Кроме того,и, значит (см. рис. 10.8),.

Следовательно, и числитель, и знаменатель производной в формуле (10.8) положительны, положительна и сама производная, т. е.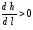. Это означает, что глубина потока вдоль движения возрастает. В зонеa глубина может изменяться от нормальной глубины до теоретически бесконечно большой. Вверх по потоку кривая свободной поверхности асимптотически приближается к линии нормальных глубин, т. е. к линии свободной поверхности равномерного потока. Вниз по течению линия свободной поверхности стремится к горизонтальной прямой и большим глубинам. Она имеет вогнутую форму. Такие кривые называютсякривой подпора типа a₁. Такую форму имеют кривые свободной поверхности перед плотиной или другой преградой в русле (рис. 10.1.а).

Зона b

В этой зоне , а значит. Но, следовательно,. Тогда производная, т. е. глубина потока вдоль движения уменьшается от нормальной до критической. Вверх по течению кривая сближается с линией нормальных глубин, а вниз по течению она подходит к линии критических глубин под углом, близким к прямому. Кривая свободной поверхности в этом случае имеет выпуклую форму и называетсякривой спада типа b₁. Такую форму свободной поверхности может иметь поток перед уступом или перепадом в дне русла (рис. 10.1.б).

Зона c

В этом случае и. Кроме того, в этой зоне. В соответствии с уравнением (10.8) производная. Следовательно, глубина вдоль течения возрастает от какой-то начальной глубиныh вверху по течению до критической глубины. Кривая свободной поверхности подходит к линии критической глубины под углом, близким к прямому, имеет вогнутый характер и называется кривой подпора типа c₁. Такая линия поверхности может устанавливаться непосредственно за плотиной или щитом (рис. 10.1.в). При падении воды с высоты в потоке устанавливаются большие скорости и малые глубины, которые возрастают при дальнейшем движении воды.

Заметим, что в случае, когда в потоке за плотиной на некотором расстоянии устанавливается равномерное движение, переход к нему в плавноизменяющемся режиме невозможен. Действительно, глубина потока должна увеличиться от малого значения h до критической глубины (в зонеc), а затем – до нормальной глубины h₀ в зоне b. Но в зоне b, согласно уравнению (10.8) и вышеизложенным рассуждениям, при плавноизменяющемся режиме течения устанавливается только кривая спада и глубина повышаться не может. В этом случае возможен не плавный, а резкий скачкообразный переход от бурного состояния потока к спокойному; такой переход называется гидравлическим прыжком.