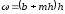2. Равномерное движение в открытых руслах. Основные задачи при расчете равномерного движения.

Движение в каналах трапецеидального поперечного сечения характеризуется двумя группами величин:

• величины, определяющие геометрические размеры живого сечения – b, h и m;

• величины, определяющие гидравлический режим течения – n, I и Q .

Условиями проектирования, как правило, задаются значения всех величин, кроме одной. Задача гидравлического расчета состоит в отыскании неизвестной характеристики.

Рассмотрим несколько типичных примеров гидравлического расчета, связанных с проектированием каналов.

1. Геометрия живого сечения задана.

1.1. Пусть заданы все размеры живого сечения, т. е. b, h и m и также уклон дна I₀ и коэффициент шероховатости n. Требуется определить расход Q воды в канале.

Задачу решаем следующим образом:

• зная размеры живого сечения, находим его площадь , величину смоченного периметраи гидравлический радиус;

• зная R и n, по формулам Павловского (4.8) или Маннинга (4.9) определяем C;

• зная C и R, определяем скорость течения ;

• зная и, находим искомый расход.

1.2. Пусть заданы размеры живого сечения, (т. е. b, h и m), а также коэффициент шероховатости n и расход Q. Необходимо найти уклон дна в канале I₀.

Ход решения:

• так же, как и выше, находим величины ,,R, C;

• зная , рассчитываем скорость течения;

• по формуле (9.3) вычисляем уклон .

2. Расчет элементов геометрии канала.

Задачи по определению геометрических размеров трапецеидального канала решаются путем подбора искомой величины.

Пусть заданы m, b, n, I₀, Q. Требуется найти глубину наполнения канала h. (Вариант – задана h, необходимо определить b).

Ход решения:

• рассчитываем модуль расхода K_треб, которым должен характеризоваться канал:;

• строим график зависимости модуля расхода K от глубины наполнения h: задаваясь рядом значений глубины h, рассчитываем для каждого h соответствующий модуль расхода; для этого удобно составить таблицу расчета:

• по данным такой таблицы (по строкам 1 и 6) строим график зависимости – рис. 9.5.а; кривая имеет выпуклость, обращенную в сторону оси h, и проходит через начало координат (при h = 0 значение K = 0);

• по этому графику, зная K_треб, находим искомую глубину наполнения канала h _иск;

• в случае если задана глубина наполнения h и требуется отыскать ширину по дну b, расчет производится с использованием тех же зависимостей таблично-графическим способом; строится график (рис. 9.5.б) и по нему определяется b _иск.

Рис. 9.5

3. Среди заданных величин – средняя скорость.

3.1. Пусть заданы размеры живого сечения, т. е. b, h и m, а также n и . Требуется найтиQ и I₀.

Ход решения:

• вычисляем площадь живого сечения , величину смоченного периметраи гидравлический радиус;

• находим расход ;

• зная R и n, определяем C;

• определяем уклон дна .

3.2. Пусть заданы m, n, Q, , а также одна из величин:h или b. Требуется определить: уклон дна I₀, а также неизвестный геометрический размер b или h.

Ход решения:

• вычисляем площадь живого сечения ;

• формула для площади живого сечения содержит одну неизвестную величинуb или h (в зависимости от условий задачи); решая это уравнение, находим неизвестный геометрический размер живого сечения;

• рассчитывая необходимые величины (R и C), определяем уклон дна .

Таблица 9.1

Расчет геометрических параметров канала

№	Величина	Задаваемые и расчетные значения
1.	h	h1	h2	. . .	. . .	. . .	hn
2.		. . .	. . .	. . .	. . .	. . .	. . .
3.		. . .	. . .	. . .	. . .	. . .	. . .
4.		. . .	. . .	. . .	. . .	. . .	. . .
5.	(формула Маннинга)	. . .	. . .	. . .	. . .	. . .	. . .
6.		. . .	. . .	. . .	. . .	. . .	. . .