4. Анализ простых электрических цепей постоянного тока

К простым электрическим цепям относятся неразветвленные цепи и такие разветвленные цепи, у которых один или несколько источников расположены в одной ветви. Анализ простых электрических цепей можно выполнять на основе закона Ома. Типичными примерами простых электрических цепей являются последовательное, параллельное и смешанное соединения пассивных элементов.

Схема последовательного соединения двух пассивных элементов в цепи постоянного тока приведена на рис. 14.

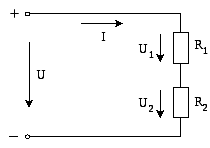
Рис. 14. Схема последовательного соединения двух

пассивных элементов в цепи постоянного тока

При последовательном соединении элементов через них протекает один и тот же ток. Известными величинами на схеме являются входное напряжение Uи сопротивления пассивных элементовR₁ и R₂. Требуется определить токI, напряжения на элементахU₁ иU₂, мощностиP₁ иP₂отдельных элементов и мощность P, потребляемую всей схемой.

Схема рис. 14 является неразветвленной одноконтурной. В соответствии со вторым законом Кирхгофа для этой схемы справедлива формула

или

где R_вх= R₁ + R_2.

Эквивалентное сопротивление R_вхназывается входным сопротивлением схемы. При последовательном соединении элементов входное сопротивление схемы равно сумме сопротивлений этих элементов.

Зная входное сопротивление схемы, с помощью закона Ома можно найти ток в схеме

Напряжения на отдельных элементах схемы распределяются пропорционально их сопротивлениям

Мощности, потребляемые элементами и цепью в целом, определяются с помощью закона Джоуля-Ленца

Мощность, потребляемая цепью, равна сумме мощностей, потребляемых ее элементами

Р = Р₁ + Р₂.

Это правило является следствием закона сохранения энергии и носит название баланса мощностей. Проверка выполнения баланса мощностей широко используется в электротехнике для контроля правильности расчета токов.

Анализируя выражения мощностей, потребляемых элементами и цепью в целом, и выражение баланса мощностей, можно дать следующее определение для входного сопротивления схемы: входное сопротивление схемы – это такое эквивалентное сопротивление, которое потребляет такую же мощность, что и исходная схема.

Схема параллельного соединения двух пассивных элементов в цепи постоянного тока приведена на рис. 15. При параллельном соединении элементов все они находятся под действием одного напряжения U. Известными величинами в схеме являются входное напряжениеU, сопротивления или проводимости пассивных элементовR₁ = 1/g₁,R₂= 1/g₂. Требуется определить токI, потребляемый из сети, токи параллельных ветвейI₁ иI₂, мощностиР₁ и Р₂отдельных элементов и мощностьР, потребляемую всей схемой.

Рис. 15. Схема параллельного соединения двух

пассивных элементов в цепи постоянного тока

В соответствии с первым законом Кирхгофа для узла aсхемы рис. 15 справедлива формула

I = I₁ + I_2..

Используя закон Ома для участка цепи постоянного тока с пассивным элементом, эту формулу можно записать иначе

или

где

Эквивалентная проводимость g_вх называется входной проводимостью схемы. При параллельном соединении элементов входная проводимость схемы равна сумме проводимостей этих элементов.

При известной входной проводимости схемы ток, потребляемый из сети, определяется с помощью закона Ома

I = g_вх U.

Токи параллельных ветвей пропорциональны их проводимостям

I₁ = g₁ U; I₂ = g₂ U.

Мощности, потребляемые элементами и цепью в целом, определяются с помощью закона Джоуля-Ленца

Мощности ветвей пропорциональны проводимостям ветвей. Мощность, потребляемая цепью, равна сумме мощностей, потребляемых ее элементами

Р = Р₁ + Р_2..

Схема смешанного соединения пассивных элементов в цепи постоянного тока приведена на рис. 16.

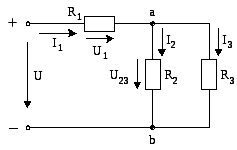
Рис. 16. Схема смешанного соединения пассивных элементов

в цепи постоянного тока

В этой схеме два пассивных элемента включены параллельно и один последовательно с ними. Известными величинами в схеме являются входное напряжение Uи сопротивления пассивных элементовR₁,R₂,R₃. Требуется определить токи ветвейI₁, I₂,I₃, напряженияU₁,U₂, мощности отдельных элементов Р₁,Р₂,Р₃и мощность Р, потребляемую всей схемой.

Анализ схемы выполняют путем ее последовательного упрощения. Сначала определяют эквивалентную проводимость параллельного соединения элементов

и соответствующее ей эквивалентное сопротивление

Сопротивление R₁и эквивалентное сопротивление параллельного участкаR₂₃включены последовательно. Поэтому входное сопротивление схемы равно

(6)