16. Баланс мощностей

В соответствии с законом сохранения энергии в любой электрической цепи энергия, вырабатываемая всеми источниками в единицу времени, равна энергии, потребляемой приемниками электрической энергии в единицу времени. Т.е. в электрических цепях энергетический баланс можно свести к балансу мощностей.

Рассмотрим обобщенную электрическую цепь постоянного тока произвольной конфигурации, с произвольным числом источников электрической энергии и произвольным числом приемников электрической энергии. Если все источники являются источниками ЭДС, то уравнение баланса мощностей для такой цепи можно записать в виде:

.

Левая часть уравнения баланса мощностей представляет собой арифметическую сумму мощностей, обусловленных выделением тепла на сопротивлениях Rпри протекании через них токаIв соответствии с законом Джоуля-Ленца. Эта сумма охватывает все сопротивленияR электрической цепи, в том числе и внутренние сопротивления источниковR_i.

Правая часть уравнения баланса мощностей представляет собой алгебраическую сумму мощностей источников ЭДС. Выбор знака очередного члена алгебраической суммы производится в соответствии с энергетическими соотношениями, характерными для режимов генерирования и потребления электрической энергии реальным источником ЭДС, которые были рассмотрены в предыдущем параграфе. А именно: если знаки EиIодинаковы, то мощность источникаEI положительна, и он работает в режиме генерирования электрической энергии; если знакиEиIразличны, то мощность источникаEI отрицательна, и он работает в режиме потребления электрической энергии.

При наличии в схеме источников тока их мощность также необходимо учесть в правой части уравнения баланса мощностей. Предположим, что источник тока включен между узлами a иb схемы: в узелaвтекает токI_kисточника тока, а из узлаbон вытекает. Тогда на выводных зажимах источника тока будет напряжениеU_ab. Если знакиI_kиU_abодинаковы, то мощность источника токаU_abI_k положительна, и он работает в режиме генерирования электрической энергии. Если знакиI_kиU_abразличны, то мощность источника токаU_abI_k отрицательна, и он работает в режиме потребления электрической энергии.

С учетом изложенного уравнение баланса мощностей для цепи, содержащей как источники ЭДС, так и источники тока, можно записать в следующем виде:

.

Уравнения баланса мощностей удобно использовать для проверки правильности расчета токов в ветвях электрической цепи.

Пример 7. Проверить правильность расчета токов в примере 3 для схемы рис. 31 путем составления баланса мощностей.

Решение

Составляем уравнение баланса мощностей для схемы рис. 31:

R₁ I₁² + R₂ I₂² + R₃ I₃² + R₄ I₄² + R_i4 I₄² + R₅ I₅² + R₆ I₆² + R_i6 I₆² = E₄I₄ + E₆I₆.

Подставляем численные значения:

6∙2,82² + 10∙0,96² + 2∙1,86² + 7∙1,69² + 1∙1,69² + 8∙0,73² + 9∙1,13² + 1∙1,13² =

= 40∙1,69 + 32∙1,13.

Производя вычисления, получаем:

103,7 = 103,7 Вт.

Баланс мощностей сошелся. Токи рассчитаны правильно.

17. Режимы работы электрических цепей постоянного тока

В настоящем параграфе рассматривается вопрос выбора возможного режима работы электрической цепи постоянного тока с точки зрения энергопотребления от генератора.

Схема обобщенной линейной электрической цепи постоянного тока представлена на рис. 1. Она состоит из источника с ЭДС Еи внутренним сопротивлениемR_iи приемника с сопротивлениемR. Источник работает в режиме генератора и отдает энергию приемнику. ЭДСЕи внутреннее сопротивлениеR_iисточника являются константами. СопротивлениеRприемника величина переменная. Изменяя величину сопротивленияRприемника, можно изменить ток в схеме. ЗависимостьI(R) при неизменных значенияхEиR_iвыражает формула закона Ома (3). Связь между напряжениемUи токомIвыражается формулой:

,

которой соответствует внешняя характеристика источника U(I), представленная на рис. 55 отрезком прямой между точками холостого хода 1 и короткого замыкания 2.

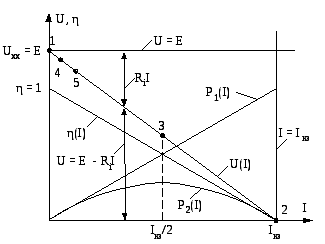
Рис. 55. Зависимости U(I), P₁(I), P₂(I), η(I) для обобщенной линейной

электрической цепи постоянного тока

Режим работы электрической цепи определяется положением рабочей точки на внешней характеристике источника. Каждой точке внешней характеристики и соответственно каждому режиму работы электрической цепи соответствуют свое напряжение Uи токI. Кроме того, каждый режим работы электрической цепи характеризуется и другими параметрами, такими как мощностьP₁ =EI, вырабатываемая источником, мощностьюP₂=UI, потребляемая приемником, КПД η =P₂/P₁. Графики зависимостейP₁(I),P₂(I), и η(I) приведены на рис. 55 наряду с внешней характеристикой. ЗависимостьP₁(I) представляет собой отрезок прямой линии, выходящий из начала координат. ЗависимостьP₂(I) – это кривая, выходящая из начала координат и приходящая в точку короткого замыкания 2. График функцииP₂(I) имеет явно выраженный экстремум. Зависимость η(I) представляет собой отрезок прямой, который строится в соответствии с формулой

.

На внешней характеристике можно выделить четыре характерных режима работы электрической цепи. Это режим холостого хода 1, режим короткого замыкания 2, так называемый согласованный режим работы 3 и номинальный режим работы. Номинальный режим – это основной расчетный режим работы электрической цепи. Положение точки номинального режима работы электрической цепи на внешней характеристике зависит от назначения электрической цепи.

В режиме холостого хода выходные зажимы источника разомкнуты (рис. 56). Сопротивление приемника в режиме холостого хода равно бесконечности (R_xx= ). Ток холостого хода равен нулю (I_xx= 0). Напряжение холостого хода равно ЭДС источника (U_xx=E). Источник не отдает энергию во внешнюю цепь (P₁= 0). Приемник энергию не потребляет (P₂= 0). КПД в режиме холостого хода максимален (η_xx= 1, см. рис.1.20). Реальные источники электрической энергии работают в режиме холостого хода только непродолжительное время. Например, перед подключением на их зажимы нагрузки или после ее снятия.

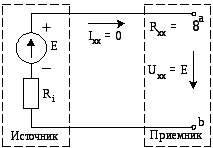
Рис. 56. Схема цепи постоянного тока, работающей

в режиме холостого хода

В режиме короткого замыкания выходные зажимы источника соединены между собой (рис. 57).

Сопротивление приемника в режиме короткого замыкания равно нулю (R_кз= 0). Ток короткого замыкания достигает максимально возможного значения и ограничивается только внутренним сопротивлением источника

.

ЭДС источника уравновешивается падением напряжения на внутреннем сопротивлении источника, то есть E=R_iI_кз. Напряжение, подводимое к приемнику, равно нулю (U_кз= 0). МощностьP₁, вырабатываемая источником, максимальна. Энергия, вырабатываемая источником, выделяется в виде тепла на внутреннем сопротивлении источника. МощностьP₂, потребляемая приемником, равна нулю. КПД режима короткого замыкания равен нулю (η_кз= 0, см. рис. 55).

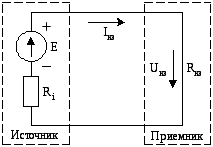
Рис. 57. Схема цепи постоянного тока, работающей

в режиме короткого замыкания

Для большинства электрических цепей (прежде всего, силовых) режим короткого замыкания неприемлем из-за нулевого КПД и нулевой мощности P₂, потребляемой приемником. Поэтому большинство электрических цепей для работы в режиме короткого замыкания не рассчитаны. Для них режим короткого замыкания является аварийным, т.к. токI_кзи мощностьP_1кз, вырабатываемая источником, в режиме короткого замыкания существенно превышают значениеI_ниP_1нноминального режима работы. Однако для некоторых слаботочных цепей режим, близкий к режиму короткого замыкания, может использовать в качестве номинального режима. Например, когда возникает необходимость в подключении приемника с малым входным сопротивлением к источнику с большим внутренним сопротивлением.

Итак, точка рабочего режима электрической цепи на внешней характеристике может лежать между точками холостого хода 1 и короткого замыкания 2 (см. рис. 55). Выбор оптимального режима работы электрической цепи зависит от назначения электрической цепи.

Для ряда цепей, например, оптимальным будет режим, при котором от источника к приемнику передается максимальная мощность. Этот режим называется согласованным режимом работы. Для установления условия передачи от источника к приемнику максимальной мощности необходимо выразить зависимость мощности P₂, выделяющейся в приемнике, от величины сопротивления приемникаR, взять производнуюdP₂/dRи приравнять ее к нулю.

Ток I(рис. 1) определяется в соответствии с законом Ома

.

Мощность P₂, выделяющаяся в приемнике, определяется законом Джоуля-Ленца

.

Производная мощности

.

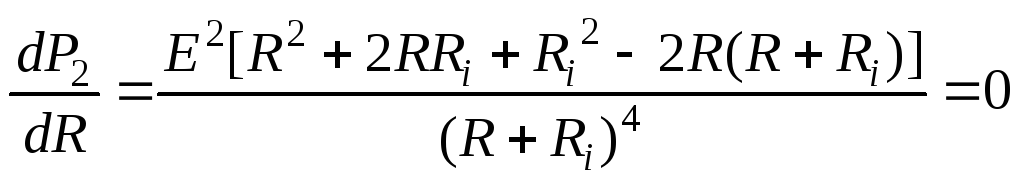Полученное выражение равно нулю, если равен нулю числитель

,

а это возможно, если сопротивление приемника Rравно внутреннему сопротивлению источникаR_i. Итак, равенствоR = R_iявляется условием передачи максимальной мощности от источника к приемнику. На внешней характеристике режиму передачи максимальной мощности соответствует точка 3 (рис. 55).

В приемнике выделяется мощность P₂ = RI², в источнике ΔP = R_iI². ЕслиR = R_i, то эти мощности одинаковы. МощностьP₂, выделяющаяся в приемнике, является полезной. Мощность ΔP, выделяющаяся в источнике, представляет собой потери мощности. Вся энергия вырабатывается источником. Поэтому в согласованном режиме полезная мощность составляет только половину от мощностиP₁ = P₂ + ΔP, вырабатываемой источником. КПД такого режима равен 50 %. Поэтому согласованный режим может быть номинальным только в цепях, для которых энергетические показатели не являются определяющими. Это слаботочные цепи, например, информационные цепи, электронные цепи устройств автоматики и другие.

Для силовых цепей при выборе номинального режима определяющим фактором являются энергетические показатели и, прежде всего, высокий КПД. Судовые силовые электротехнические устройства рассчитываются так, чтобы в номинальном режиме их КПД лежал в пределах 85–95 %. На рис. 55 этот участок расположен между точками 4–5 внешней характеристики.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учебник. – М.: Гардарики, 2002. – 638 с.

2. Основы теории цепей: Учебник для вузов/Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – М.: «Энергоатомиздат», 1989. – 528 с.

3. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990. – 544 с.

52