3. Примеры решения задач

Пример 1. Два точечных заряда 4Q и –Q закреплены на расстоянии 0,10 м друг от друга. Определить положение точечного положительного заряда Q₁ по отношению к заряду – Q, при котором заряд Q₁ будет находиться в равновесии. Силами гравитационного взаимодействия пренебречь.

Дано: 4Q; –Q; Q₁; a = 0,10 м.

Найти: x.

Решение: Заряд Q₁ будет находиться в равновесии в том случае, если векторная сумма сил, действующих на него, будет равна нулю. Это значит, что на заряд Q₁ должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (рис. 13) может быть выполнено это условие.

Рис. 13

На участке I (рис.13) на заряд Q₁ действуют две противоположно направленные силы: и. Сила, действующая со стороны заряда 4Q, в любой точке этого участка будет больше, чем сила , действующая со стороны заряда –Q, так как больший (по модулю) заряд 4Q находится ближе к заряду Q₁, чем меньший заряд – Q. Следовательно, равновесие на этом участке невозможно.

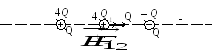
Рис. 14

Н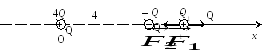а участке II (см. рис. 14) обе силыинаправлены в одну сторону к заряду –Q. Следовательно, и на втором участке равновесие невозможно.

Рис. 15

На участке III (см. рис. 15) силы инаправлены в противоположные стороны, так же как и на участкеI, но в отличие от него меньший (по модулю) заряд –Q находится ближе к заряду Q₁, чем больший заряд 4Q. Таким образом на участке III можно найти такую точку на прямой, где силы ибудут одинаковы по модулю, то есть

|| = ||.

Проведём ось x через заряды. Начало отсчёта выберем в точке, где расположен заряд 4Q.

Пусть искомое расстояние от меньшего заряда до заряда Q₁ равно х, тогда расстояние от большего заряда будет, а + х. Выразим F₁, и F₂, используя закон Кулона:

.

Решая это уравнение, найдем:

x₁ = a и x₂ = – a/3.

Корень x₂ не удовлетворяет условию задачи (в этой точке силы F₁ и F₂ хотя и равны по модулю, но расположены в области II).

Окончательно получаем

x = a.

Тогда

x = 0,1 м.

Ответ: x = 0,1 м.

Пример 2. Два точечных заряда 0,20 нКл и –0,30 нКл находятся на расстоянии 0,50 м друг от друга в вакууме. Найти напряжённость и потенциал результирующего электростатического поля в точке, находящейся на расстоянии 0,40 м от первого заряда и 0,20 м от второго.

Дано: q₁ = 0,20 нКл; q₂ = – 0,30 нКл; a = 0,50 м; r₁ = 0,40 м; r₂ = 0,20 м.

Найти: E; .

Решение: Напряжённость и потенциал результирующего электростатического поля, создаваемого зарядами, рассчитаем по принципу суперпозиции:

и  = ₁ + ₂.

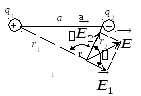
Рис. 16

Учитывая, что напряжённость электростатического поля является векторной величиной, рассчитаем модуль вектора по теореме косинусов (рис. 16)

. (1)

Угол  = 180 – . Согласно формулам приведения тригонометрии cos = cos(180 – ) = – cos. По теореме косинусов

.

Тогда . (2)

В данном случае во избежание громоздких записей вычислим отдельно значение cos. По формуле (2) найдём

.

Модули напряжённостей полей, создаваемых точечными зарядами q₁ и q₂, определяются по формулам:

; . (3)

Потенциалы полей, создаваемых точечными зарядами q₁ и q₂, в заданной точке определяются по формулам:

; . (4)

С учётом зависимостей (1), (3) и (4) получаем конечные формулы для вычисления величин Е и :

.

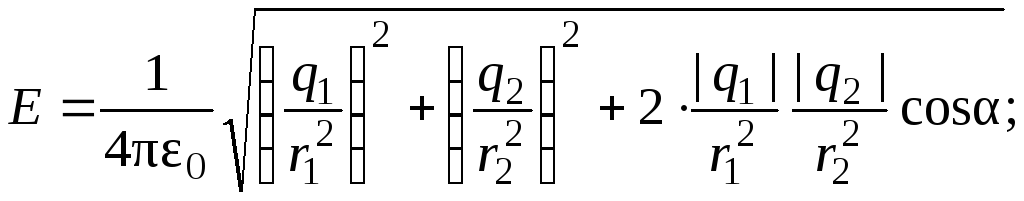
Произведём вычисления напряжённости результирующего поля, учитывая, что k == 910⁹ (Нм²)/Кл²:

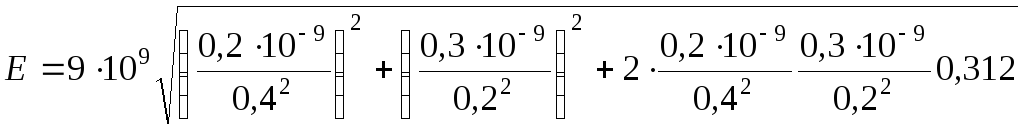= 82,1 В/м.

Произведём вычисления потенциала результирующего поля

Ответ: Е = 82,1 Н/Кл;  = – 9 В.

Пример 3. Электростатическое поле создаётся бесконечно длинной заряженной нитью с линейной плотностью заряда 1,00 мкКл/м. Определить модуль напряжённости поля в точке, находящейся на расстоянии 0,20 м от нити.

Дано: = 1,00 мкКл/м = 1,0010^–6 Кл/м; x = 0,20 м.

Найти: E.

Решение: Воспользуемся принципом суперпозиции электростатических полей. Так как нить не точечный заряд, то проведём расчёт искомой величины методом дифференцирования. Для этого разобьем нить на бесконечно малые участки длиной dy (см. рис. 17). Каждый такой участок имеет заряд dq и создаёт в точке О электростатическое поле с напряжённостью .

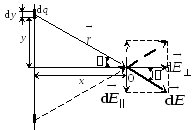
Рис. 17

Заряд участка dy определяется выражением

,

где  – линейная плотность заряда ( = q/).

Вектор напряжённости разложим на две составляющие

.

Величины этих составляющих dE_ и dE_|| определяются по формулам:

dE_=dE; dE_|| =dE .

Модуль напряжённости поля, создаваемого зарядом dq можно рассчитать по формуле для точечного заряда. Тогда

.

Напряжённость поля всей нити (по принципу суперпозиции) рассчитывается по формуле

,

где второе слагаемое обращается в ноль из соображений симметрии, а в первом необходимо учесть, что составляющие всех элементовdy сонаправлены (рис. 17).

Тогда векторное интегрирование можно заменить скалярным

.

Выполним тригонометрические преобразования:

Окончательно получаем

.

Произведём вычисления:

Ответ: Е = 9,00 МВ/м.

Пример 4. Рассчитать потенциал электростатического поля на оси равномерно заряженного кольца. Заряд кольца 10,00 мкКл, радиус 0,01 м. Расстояние от оси кольца до рассматриваемой точки 0,20 м.

Дано: q = 10,00 мкКл = 1010^{– 6} Кл; R = 0,01 м; x₀ = 0,20 м.

Найти:.

Решение: Воспользуемся принципом суперпозиции электростатических полей. Для этого разобьем кольцо на бесконечно малые участки длиной d (рис. 18).

Каждый такой участок имеет заряд dq и создаёт в точке электростатическое поле с потенциаломd. Заряд dq можно рассматривать как точечный, Рис. 18

тогда потенциал d можно определить по формуле

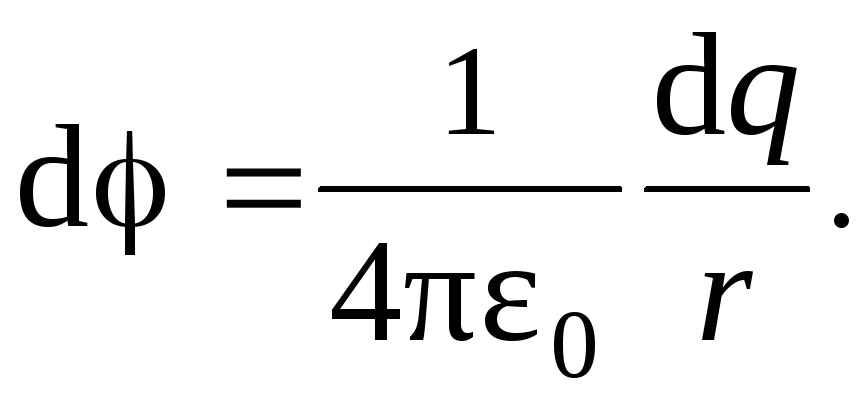(1)

Рассчитаем потенциал поля, создаваемого всем кольцом используя принцип суперпозиции.

Для этого проинтегрируем выражение (1), учитывая, что x₀ = const; r = const:

.

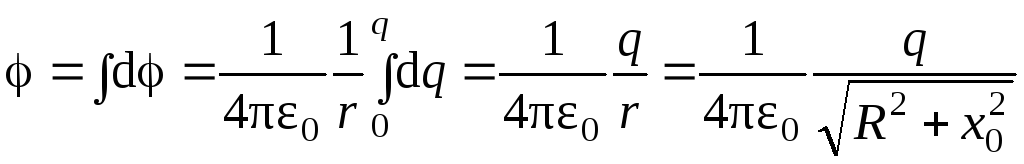Произведём вычисления:

.

Ответ:  = 0,45 МВ.

Пример 5. Рассчитать потенциал электростатического поля на оси равномерно заряженного диска. Заряд диска 10,00 мкКл, радиус 0,01 м. Расстояние от центра диска до рассматриваемой точки 0,20 м.

Дано: q = 10,00 мкКл = 1010^–6 Кл; R = 0,01 м; x₀ = 0,20 м.

Найти: .

Р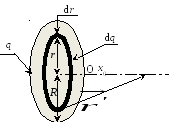ешение: Используем для решения этой задачи результаты, полученные в примере 4. Мысленно выделим на диске кольцо, внутренний радиус которого равен r, а наружный – r + dr (рис. 19).

Рис. 19

Заряд такого кольца ,

где – поверхностная плотность заряда;– площадь поверхности кольца.

Тогда

. (1)

Согласно принципу суперпозиции искомый потенциал в точке

. (2)

Подставим выражение (1) в (2) и проинтегрируем:

.

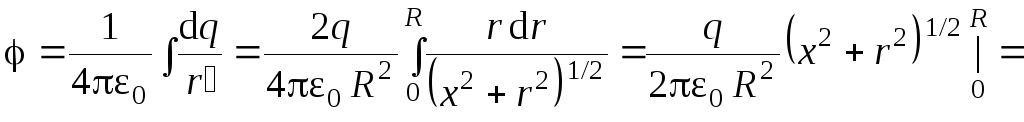
Произведём вычисления:

Ответ:  = 0,45 МВ.

Пример 6. В вакууме из бесконечности движутся два электрона навстречу друг другу, вдоль одной прямой. Определить минимальное расстояние, на которое частицы смогут приблизиться, если их начальные скорости равны 10⁵м/с и 2∙10⁵м/с. Гравитационным взаимодействием пренебречь.

Дано: q_e =1,610^–19 Кл; m_e = 9,110^–31 кг; = 10⁵ м/с; =2∙10⁵ м/с.

Найти: r_min.

Решение: Запишем закон сохранения энергии для ситуаций, когда частицы находятся на бесконечном удалении и на минимальном расстоянии друг от друга.

На бесконечном удалении электроны не взаимодействуют друг с другом, поэтому энергия системы приходится на начальные кинетические энергии зарядов

.

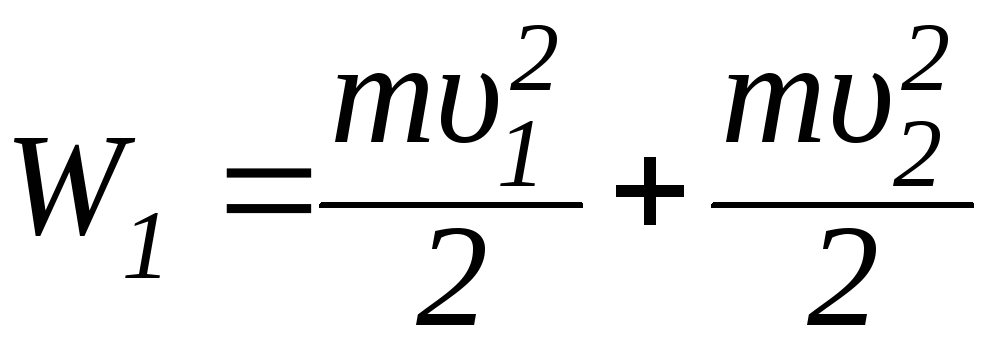При сближении электроны начинают взаимодействовать так. Это приведёт к торможению зарядов. Электрон, обладающий меньшей скоростью, остановится и начнёт движение в обратном направлении. Второй электрон продолжит движение в прежнем направлении. Частицы продолжают сближаться, при этом скорость первой частицы возрастает, второй – убывает. В соответствии с теоремой о движении центра масс, сближение зарядов будет происходить до тех пор, пока их скорости не станут одинаковыми. В этом состоянии полная энергия системы приходится на потенциальную энергию электростатического взаимодействия и кинетические энергии движения частиц (которые одинаковы). Тогда

.

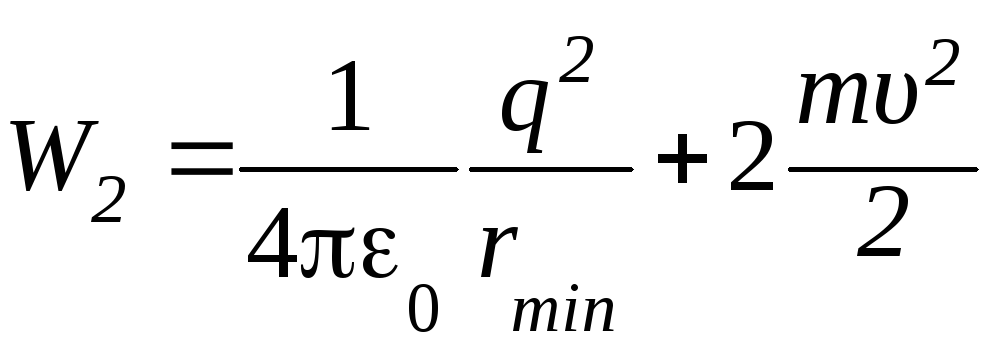где – конечная скорость, с которой частицы будут двигаться в одном направлении равномерно и прямолинейно.

Запишем закон сохранения энергии

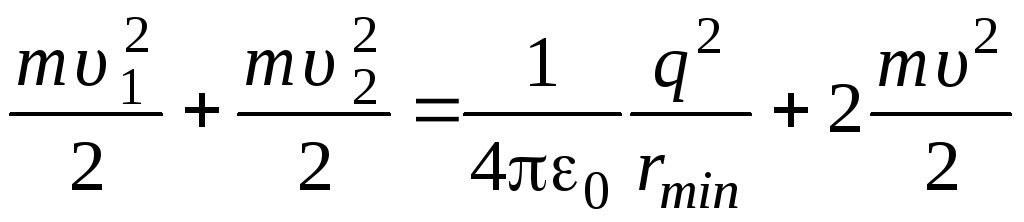, (1)

Запишем закон сохранения импульса для этих же ситуаций

. (2)

Решаем совместно уравнения (1) и (2), учитывая, что. В результате получаем:

.

Произведём вычисления:

.

Ответ: r_min = 1,1210^–2 м.

Пример 7. Электрон, предварительно ускоренный разностью потенциалов 0,10 кВ, влетел в середину плоского воздушного конденсатора параллельно его пластинам. Расстояние между пластинами конденсатора 0,04 м, длина пластин 0,10 м. Определить минимальное напряжение, которое необходимо приложить к конденсатору, чтобы электрон из него не вылетел. Доказать, что частица движется в конденсаторе по параболической траектории. Действием силы тяжести пренебречь.

Дано: q_e=1,610^–19Кл; m_e = 9,110^–31 кг; U₁ = 0,10кВ; d = 0,04м; b = 0,10м.

Найти: U₂.

Решение: В ускоряющем электростатическом поле над электроном совершается работа, которая приводит к приращению его кинетической энергии. По закону сохранения энергии можно записать

,

где – скорость, с которой частица влетает в электростатическое поле конденсатора.

По принципу суперпозиции можно рассматривать движение электрона в конденсаторе как независимое наложение двух движений (рис. 20):

• равномерное движение вдоль оси X со скоростью ;

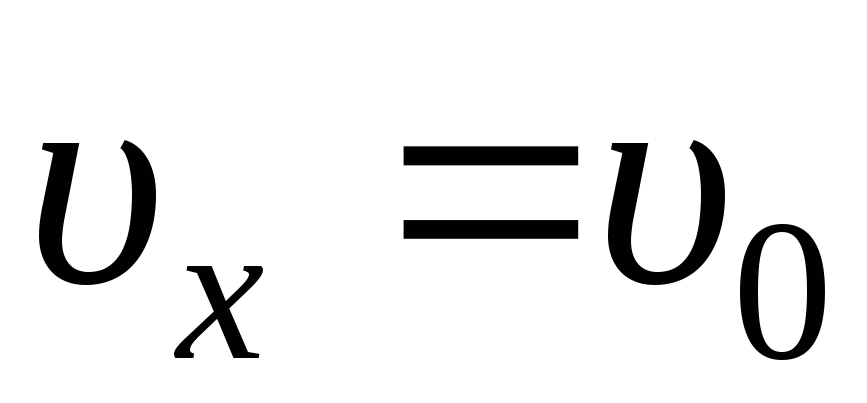• равнопеременное движение вдоль оси Y с ускорением, сообщаемым силой электростатического поля конденсатора ().

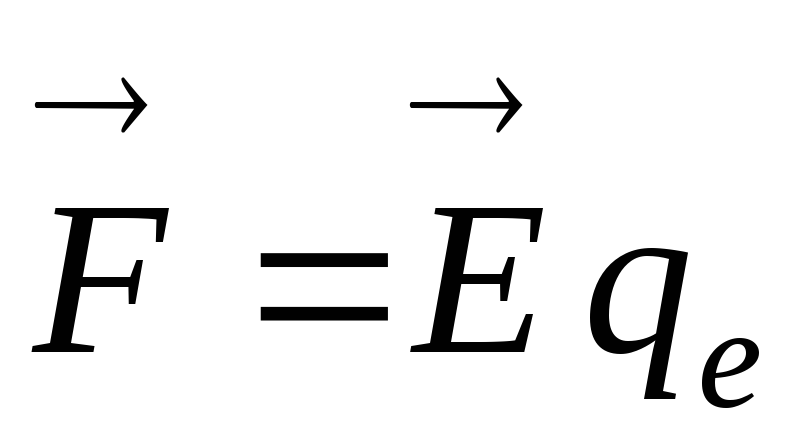Вычислим ускорение частицы с помощью второго закона Ньютона

.

Здесь мы использовали связь между напряжением U и напряжённостью E в однородном электростатическом поле:

U = E d.

Координаты x и y электрона изменяются по законам:

x = ₀ t; (1)

y = a_у t²/2 = q_еU₂ t ²/2m_e . (2)

Э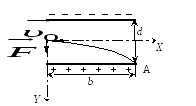лектрон не вылетит из конденсатора, если попадёт в точку А, находящуюся на краю пластины (см. рис. 20).

Рис. 20

Для точки А x = b; y = d/2.

Подставим эти значения в (1) и (2) и, решая уравнения совместно, найдём напряжение U₂:

U₂ =.

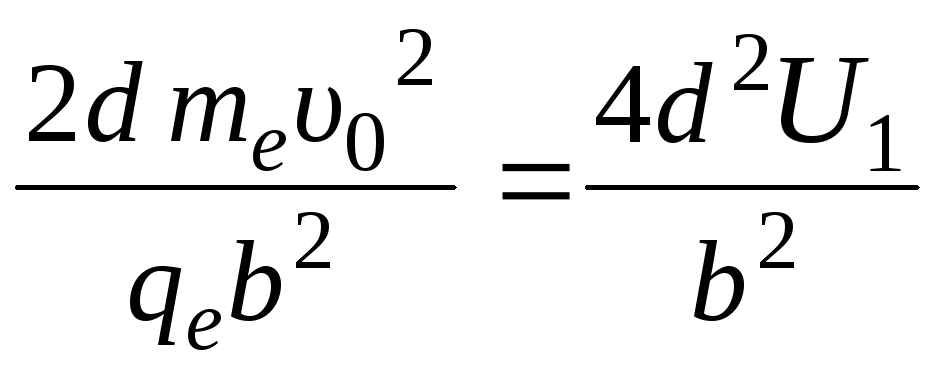Произведём вычисления:

.

Для доказательства того, что движение электрона происходит по параболической траектории, получим уравнение его траектории. Используя формулы (1) и (2), получаем

.

Так как ускорение а_у и скорость являются константами, то получаем:

y = const x² (уравнение параболы).

Ответ: U₂ = 32 В; электрон движется в конденсаторе по параболической траектории.

Пример 8. Две концентрические проводящие сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды q₁ = l нКл и q₂ = – 0,5 нКл. Пространство между сферами полностью заполнено диэлектриком с диэлектрической проницаемостью  = 2. Найти напряженность электрического поля в точках, отстоящих от центра сфер на расстояниях r₁ = 5 см, r₂ = 9 см r₃ = 15см.

Дано: R₁ = 0,06 м; R₂ = 0,10 м; q₁ = 1,010^–9 Кл; q₂ = – 0,510^–9 Кл; r₁ = 0,05 м, r₂ = 0,09 м r₃ = 0,15 м.

Найти: E₁; E₂; E₃.

Р

r₂

ешение: Точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 21):

• область I (r₁ < R₁);

• область II (R₁ < r₂ < R₂);

• область III (r₃ > R₂).

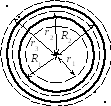
Рис. 21

Для определения напряженности воспользуемся теоремой Гаусса.

1. Для определения напряженности E₁ в области I проведем сферическую поверхность площадью S₁ радиусом r₁ и рассчитаем поток вектора напряжённости через выбранную гауссовскую поверхность. Так как внутри области I зарядов нет, то согласно указанной теореме получим равенство

или , (1)

где E_n1 – нормальная составляющая вектора напряженности электрического поля в точках области I.

Так как произведение равно 0, а , тоE₁ = 0, т. е. напряженность поля во всех точках, удовлетворяющих условию r₁<R₁, будет равна нулю.

2. В области II поток вектора напряжённости электрического поля рассчитаем через сферическую поверхность площадью (рис. 21). Так как внутри этой поверхности находится зарядq₁, то для нее, согласно теореме Гаусса, можно записать равенство

или ,

где E_n2 – нормальная составляющая вектора напряженности электрического поля в точках области II.

Так как E_n = Е₂ = const, то

,

.

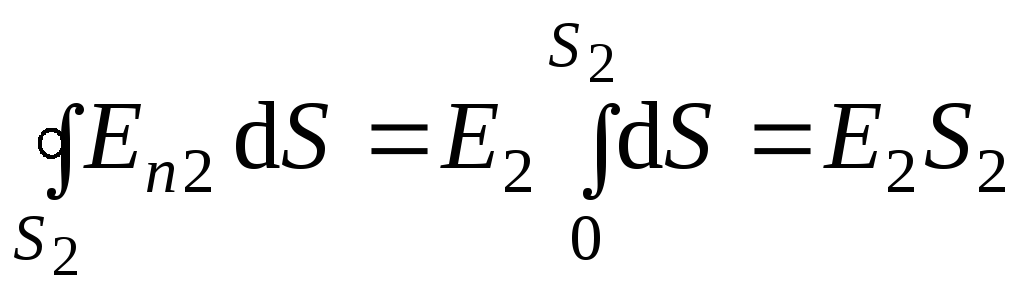Тогда . (2)

3. В области III поток вектора напряжённости электрического поля рассчитаем через сферическую поверхность площадью (рис. 21). Эта поверхность охватывает суммарный заряд q₁+q₂. Следовательно, для нее уравнение, записанное на основе теоремы Гаусса, будет иметь вид

.

Тогда, используя положения, примененные в первых двух случаях, найдем

(3)

Убедимся в том, что правые части равенств (2) и (3) дают единицу напряженности электрического поля:

.

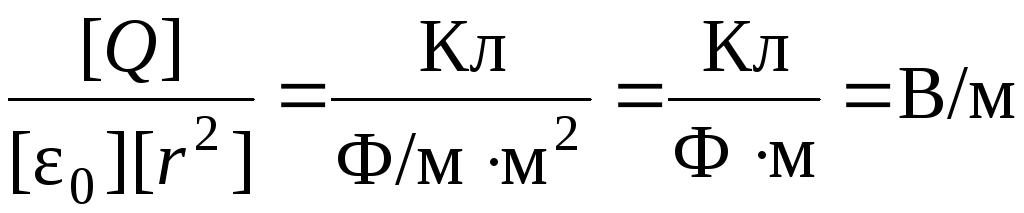Произведем вычисления:

;

.

Ответ: E₁ = 0 В/м; E₂ = 560 В/м; E₃ = 200В/м.

Пример 9. Плоский воздушный конденсатор электроёмкостью С заполняют наполовину диэлектриком с диэлектрической проницаемостью  = 2, как показано на рис. 22. Определить, во сколько раз изменится электроёмкость конденсатора.

Рис. 22

Дано:  = 2.

Найти: С_посл./С_.; С _пар./С.

Решение: 1. Исходный конденсатор имеет электроёмкость, которая рассчитывается по формуле

где  = 1, т.к. конденсатор воздушный.

Тогда

Рассмотрим конденсатор, наполовину заполненный диэлектриком первым способом (рис. 22 (а)). Такой конденсатор можно рассматривать как два конденсатора с ёмкостями и, соединённые последовательно (рис. 23).

Рис. 23

Электроёмкость С_посл. двух последовательно соединённых конденсаторов равна

,

где так как у этих конденсаторов расстояние между обкладками уменьшилось по сравнению с исходным в 2 раза, а диэлектрическая проницаемость диэлектрика второго конденсатора = 2 .

Для общей ёмкости получим

.

Таким образом, электроёмкость конденсатора в первом случае увеличилась в 4/3 раза.

2. Рассмотрим конденсатор, наполовину заполненный диэлектриком вторым способом (рис. 22(б)). Такой конденсатор можно рассматривать как систему двух конденсаторов с ёмкостями и, соединённых параллельно (рис. 24).

Рис. 24

Электроёмкость полученной батареи рассчитывается по формуле

,

где так как у этих конденсаторов площадь обкладок уменьшилось по сравнению с исходным в 2 раза, а диэлектрическая проницаемость диэлектрика второго конденсатора = 2.

Для общей ёмкости получим

.

Таким образом, электроёмкость конденсатора во втором случае увеличилась в 3/2 раза.

Ответ: С_посл../С = 4/3; С _пар/./С =3/2.

Пример 10. Плоские воздушные конденсаторы электроёмкостью 5 мкФ и 10 мкФ заряжены до напряжений соответственно 100 В и 200 В. Оба конденсатора отключены от источников питания и соединены параллельно между собой в первом случае одноимёнными обкладками (рис. 25), во втором случае разноимёнными (рис. 26). Определить величину заряда, перетёкшего с обкладок одного на другой конденсатор.

Дано: С₁ = 5мкФ; С₂ = 10мкФ; U₁ = 100 B; U₂ = 200 B.

Найти: q.

Решение: 1. Рассмотрим состояние конденсаторов до и после соединения:

до и,

где q₁, q₂ – заряды конденсаторов до соединения;

после и,

Рис. 25

где ,– заряды конденсаторов после соединения;U – напряжение на конденсаторах после соединения (после соединения конденсаторов потенциалы на одноимённых обкладках выравниваются, и напряжения на конденсаторах становятся одинаковыми).

Заряд, перетёкший с обкладок одного конденсатора на другой, найдём по формуле

.

Напряжение U найдём из закона сохранения заряда:

;

С₁U₁ + С₂U₂= С₁U + С₂U;

.

Окончательно получаем

.

Произведем вычисления:

.

2. Аналогичным образом рассмотрим состояние конденсаторов до и после соединения:

до и,

где q₁, q₂ – заряды конденсаторов до соединения;

после и,

Рис. 26

где ,– заряды конденсаторов после соединения;U – напряжение на конденсаторах после соединения (после соединения конденсаторов потенциалы на соединённых разноимённых обкладках выравниваются, и напряжения на конденсаторах становятся одинаковыми).

Заряд, перетёкший с обкладок одного конденсатора на другой, найдём по формуле

.

Напряжение U найдём из закона сохранения заряда,

,

учитывая, что конденсаторы соединяются разноимёнными обкладками

С₂U₂ – С₁U₁= С₁U + С₂U;

.

Окончательно получаем

.

Произведем вычисления:

.

Ответ: 1) q = 333 мкКл; 2) q = 1000 мкКл.

Пример 11. Определить заряд, прошедший по проводу с сопро­тивлением 3,00 Ом при равномерном нарастании напряжения на концах провода от 2,00 В до 4,00 В в течение 20,00 с.

Дано: R = 3,00 Ом; U₀ = 2,00 В; U = 4,00 В, t = 20,00 с.

Найти: q.

Решение: Так как сила тока в проводе изменяется, то вос­пользоваться для подсчета заряда формулой q=I t нельзя. Поэтому возьмем заряд , проходящий через поперечное сечение проводника за малый промежуток времениdt, и проинтегрируем:

. (1)

Напряжение в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой

U= U₀+k t, (2)

где k – коэффициент пропорциональности.

Подставив это выражение в формулу (1), найдем

.

Проинтегрировав, получим

. (3)

Значение коэффициента k найдем из формулы (2):

.

Произведём вычисления k:

.

Подставив значения величин в формулу (3), получим

.

Ответ: q = 20 Кл.

Пример 12. Источники тока с электродвижущими силами и включены в цепь, как показано на рис. 27.

Рис. 27

Определить силы токов, текущих в сопротивлениях R₂ и R₃, если = 10,00 В и = 4,00 В, а R₁=R₄=2,00 0м и R₂=R₃= 4,00 Ом. Сопротивлениями источников тока пренебречь.

Дано: = 10,00 В; = 4,00 В; R₁=R₄=2,00 0м; R₂=R₃= 4,00 Ом.

Найти: I₂; I₃.

Решение: Силы токов в разветвленной цепи определяют с помощью законов Кирхгофа. В нашем случае по ветвям цепи протекают четыре различных тока, поэтому для нахождения четырёх значений силы токов следует составить четыре уравнения.

Указание. Перед составлением уравнений по закону Кирхгофа необхо­димо выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, выбрать на­правление обхода контуров (последнее только для составления уравнений по второму закону Кирхгофа).

Выберем направления токов, как они показаны на рис. 27, и условимся обходить контуры по часовой стрелке. Рассматриваемая в задаче схема имеет два узла: А и В. Но состав­лять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет таким же.

При составлении уравнений по первому закону Кирхгофа необ­ходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла – со знаком минус.

По первому закону Кирхгофа для узла В имеем

I₁+I₂+I₃–I₄=0.

Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составле­ны по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовав­шая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необ­ходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлени­ем обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус;

б) если ЭДС повышает потенциал в направлении обхода контура, то есть если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае – со знаком минус.

По второму закону Кирхгофа имеем соответственно для контуров AR₁BR₂A, AR₁BR₃A, AR₃BR₄A:

I₁R₁ - I₂R₂=– ; (1)

I₁R₁ – I₃R₃= ; (2)

I₃R₃ + I₄R₄=0. (3)

Подставив в равенства (1) – (3) значения сопротивлений и ЭДС, получим систему уравнений:

I₁+I₂+I₃-I₄=0;

2I₁ – 4I₂=6;

2I₁–4I₃=10;

4I₃+2I₄=0.

Поскольку нужно найти только два тока, то удобно воспользо­ваться методом определителей (детерминантов). С этой целью пере­пишем уравнения еще раз в следующем виде:

I₁+I₂+I₃-I₄=0;

2I₁-4I₂+0+0=6;

2I₁+0-4I₃+0=10;

0+0+4I₃+2I₄=0.

Искомые значения токов найдем из выражений

I₂=Δ_I2/Δ и I₃=Δ_I3/Δ,

где Δ – определитель системы уравнений; Δ_I2 и Δ_I3 – определители, полученные заменой соответствующих столбцов определителя  столбцами, составленными из свободных членов четырех вышеприведенных уравнений.

Находим

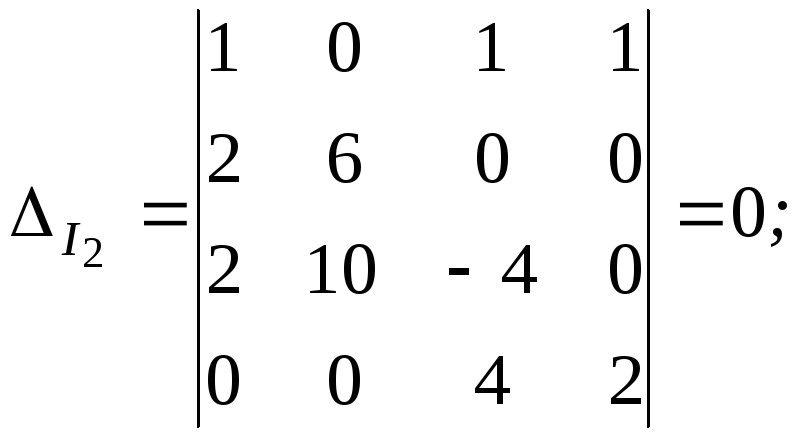
Отсюда получаем

I₂ = 0 А; I₃ = – 1 А.

Знак минус у значения силы тока I₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке 27, направление тока I₃ было указано противоположно действительному. На самом деле ток I₃ те­чет от узла В к узлу А.

Ответ: I₂ = 0 А; I₃ = – 1 А.

Пример 13. На внешнем участке цепи выделяется одинаковая мощность при двух значениях внешнего сопротивления R₁=0,20 Ом и R₂=80,00 Ом. Найти внутреннее сопротивление источника и его КПД при этих включениях.

Дано: R₁=0,20 Ом и R₂=80,00 Ом.

Найти: r; ₁, ₂.

Решение: Мощность, выделяемая на внешнем участке цепи, определяется по формуле

.

Запишем это выражение для двух состояний при включении в цепь сопротивлений R₁ и R₂:

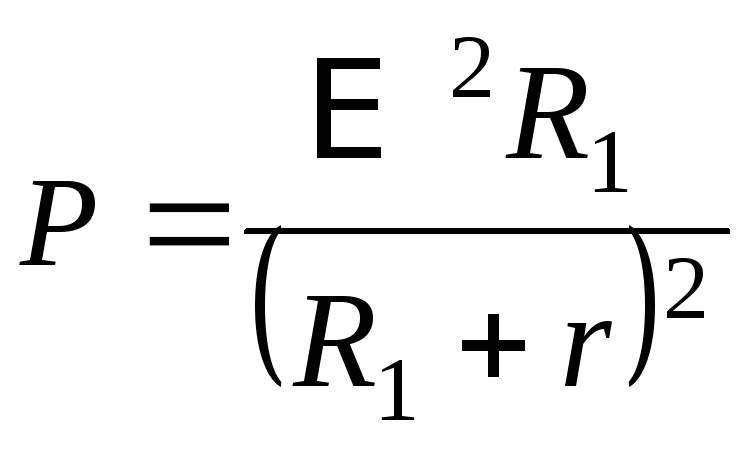и .

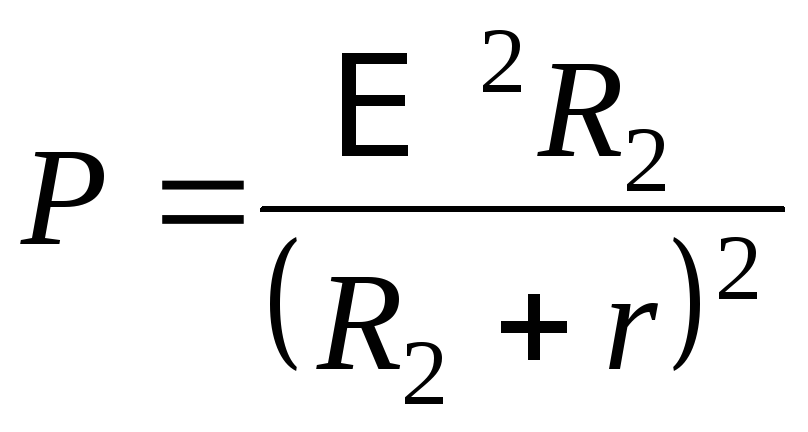Приравниваем правые части этих уравнений:

.

Проводим преобразования и выражаем внутреннее сопротивление источника тока:

;

.

Произведём вычисления:

.

КПД источника тока равен отношению полезной мощности, выделяющейся на участке цепи сопротивлением R, к полной мощности (мощности источника). Тогда

.

Произведём вычисления:

;

.

Ответ: r = 4,00 Ом; ₁=5 %; ₂ = 95 %.

Пример 14. Электрон влетел в середину плоского воздушного конденсатора параллельно его пластинам со скоростью 3,50 Мм/с. Расстояние между пластинами конденсатора 0,05 см, их длина 0,10 м. Напряжение, приложенное к конденсатору, равно 10,00 В. При вылете из конденсатора электрон попадает в однородное магнитное поле с индукцией 0,70 Тл, силовые линии которого перпендикулярны линиям напряжённости электрического поля конденсатора и вектору начальной скорости электрона. Определить скорость частицы при вылете из конденсатора и радиус окружности, по которой она будет двигаться в магнитном поле.

Дано: U = 10,00 В; d = 0,05 см; b = 0,10 м; q_e = 1,610^–19 Кл; m_e = 9,110^–31 кг; = 3,50 Мм/с;В = 0,70 Тл.

Найти: ; R.

Решение: Согласно условию задачи изобразим рисунок (рис. 28).

Рис. 28

По принципу суперпозиции можно рассматривать движение электрона в конденсаторе как наложение двух независимых движений:

• вдоль оси X, которое является равномерным, со скоростью , ();

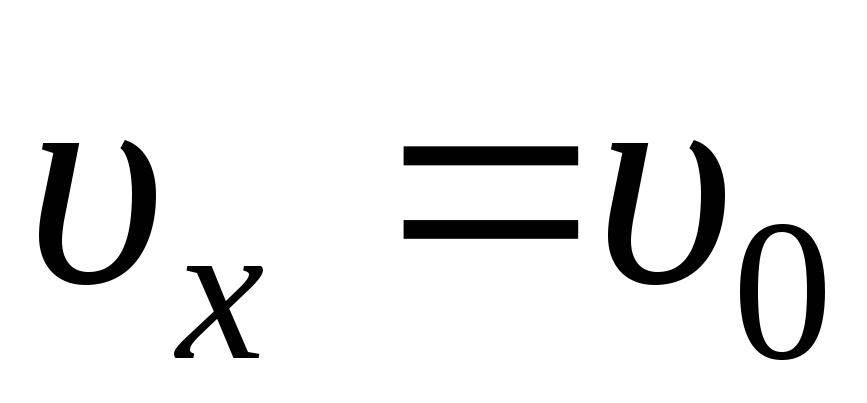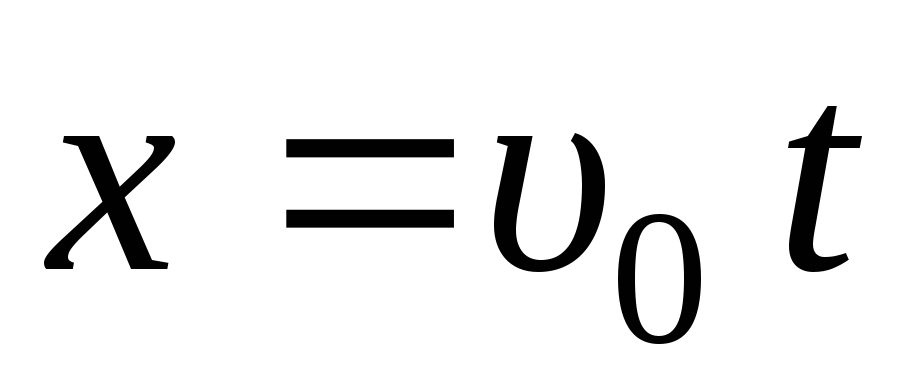• вдоль оси Y, которое является равнопеременным.

Ускорение, сообщаемое силой со стороны электростатического поля конденсатора (, силой тяжести пренебрегаем)

(см. пример 7).

Вектор скорости частицы на выходе из конденсатора направлен по касательной к параболической траектории. Модуль вектора скорости определяется через составляющие вдоль осей x и y:

,

где ;

Согласно принципу независимости движений время движения относительно оси X и оси Y одинаково. Поэтому рассмотрим движение электрона относительно оси X и выразим время его движения в конденсаторе:

Получим выражение для скорости :

.

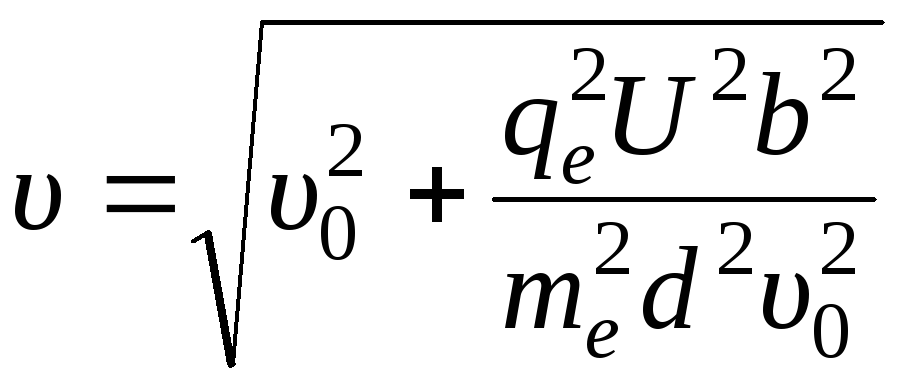Проведём вычисления:

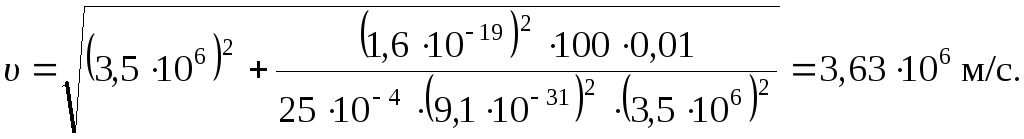
Сила Лоренца, действующая на заряженную частицу, движущуюся в магнитном поле, сообщает ей нормальное ускорение. Тогда по второму закону Ньютона

.

Используя выражения для силы Лоренца и нормального ускорения, а также учитывая, что векторы ивзаимно перпендикулярны, запишем равенство

.

Тогда радиус кривизны траектории электрона в магнитном поле

.

Проведём вычисления:

Ответ:

Пример 15. Электрон, имея скорость 1,00 Мм/с, влетел в однородное магнитное поле с индукцией 0,10 мТл под углом  = 30° к направлению линий индукции. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон.

Дано: = 1,00Mм/с; В = 0,10 мТл;  = 30.

Найти: R; h.

Решение: На заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции и скорости частицы. Её величина определяется выражением

,

где q – заряд частицы.

Так как вектор силы Лоренца перпендикулярен вектору скоро­сти, то модуль скорости не будет изменяться под действием этой силы. При постоянной скорости и значение силы Лоренца останется постоянным. Из механики известно, что постоянная си­ла, перпендикулярная скоро­сти, вызывает движение по окружности, сообщая телу нормальное ускорение. Следовательно, электрон, влетевший в маг­нитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью , равной(рис.29).

О

X

дновременно он будет двигаться и вдоль поля со ско­ростью, равной

.

X

В результате одновременного участия в движениях по окружности и Рис. 29 прямой электрон будет двигаться по винтовой линии.

Радиус окружности, по которой движется электрон, найдем по второму закону Ньютона. Сила Лоренца сообщает электрону нормальное ускорение а_п. Тогда

.

Подставив выражения силы Лоренца и нормального ускорения, получим

.

Выразим радиус кривизны траектории из предыдущего уравнения:

.

Проведём вычисле­ния:

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью за время одного оборота:

h =T,

где T=2R/– период вращения электрона.

Подставив выра­жение для Т в выражение для шага винтовой линии, получим

Проведём вычисле­ния:

Ответ:

Пример 16. В однородном магнитном поле с индукцией 0,05 Тл вращается проводящий стержень длиной 0,20 м. Угловая скорость вращения равна 5,00 с^–1. Ось вращения проходит через конец стержня и параллельна линиям магнитной индукции. Найти ЭДС индукции, возникающую на концах стержня.

Дано:  = 5,00 с^–1; = 0,20 м;В = 0,05 Тл.

Найти: .

Решение: Возникновение ЭДС на концах стержня вызвано действием силы Лоренца на электроны, движущиеся в магнитном поле вместе с проводником (стержнем). При указанных на рис. 30 направлениях поля и вращения стержня сила Лоренца направлена к оси вращения. В ту же сторону смещаются электроны. В результате этого в проводнике разделяются заряды, и возникает разность потенциалов.

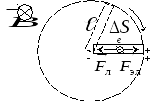
Рис. 30

Перемещение частиц происходит до тех пор, пока действие силы Лоренца не уравновесится силой, действующей на заряды со стороны индуцированного электрического поля. При этом возникает динамическое равновесие с постоянной разностью потенциалов, по модулю равной ЭДС индукции.

Тогда по закону Фарадея-Максвелла

.

Изменение магнитного потока определяется уравнением

Ф_В = ВS,

где – площадь кругового сегмента, описываемого стержнем при своём движении; = t – угол поворота стержня за время t.

Окончательно получаем

Проведём вычисления:

Ответ:

Пример 17. По двум гладким проводящим шинам, установленным под углом 30 к горизонту, скользит проводник массой 0,02 кг. Шины замкнуты на сопротивление 5,00 Ом, расстояние между ними 0,10 м. Система находится в однородном магнитном поле с индукцией 0,20 Тл, линии магнитной индукции перпендикулярны плоскости, в которой перемещается проводник (рис. 31а). Сопротивление шин, проводника и скользящих контактов, а также самоиндукция контура пренебрежимо малы. Определить величину установившейся скорости проводника.

а

Рис. 31

Дано:  = 30; m = 0,01 кг; R = 0,50 Ом; = 0,10 м;В = 0,40 Тл.

Найти: .

Р

b

Рис. 31

ешение.В начальный момент времени движение проводника вызвано действием силы тяжести. С другой стороны проводник, шины и резистор R образуют замкнутый проводящий контур, который находится в магнитном поле. Движение проводника приводит к тому, что площадь контура увеличивается. В следствие чего увеличивается магнитный поток, связанный с данным контуром. В цепи возникает электрический индукционный ток, что приводит к появлению силы Ампера (рис. 31б). В состоянии установившегося движения равнодействующая всех сил, действующих на проводник, в проекции на ось X, сонаправленную с вектором скорости равна нулю. Запишем, в проекции на эту ось, второй закон Ньютона:

0 = F_A – mg sin,

где .

Или

0 = IB– mg sin. (1)

Силу тока, проходящего по проводнику, определим по закону Ома для полной цепи

. (2)

ЭДС индукции определим по закону Фарадея-Максвелла для равномерного изменения магнитного потока

, (3)

где – приращение площади контура.

Решаем систему уравнений (1) – (3) и получаем скорость :

Проведём вычисления скорости проводника:

Ответ: