2.3. Магнитное поле

Магнитное поле создаётся либо движущимся зарядом (электрическим током), либо вихревым электрическим полем.

Силовой характеристикой магнитного поля является вектор магнитной индукции . В общем виде он определяется законом Био-Савара-Лапласа:

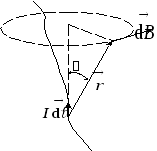
а) в векторной форме

;

б) в скалярной форме

,

Рис. 9

где – элемент тока, создающий в рассматриваемой точке магнитное поле с индукцией (рис. 9);  – магнитная проницаемость среды; ₀ – магнитная постоянная (₀ = 410^-7, Тлм/A); – радиус вектор, определяющий положение рассматриваемой точки магнитного поля по отношению к элементу тока;  – угол между элементом тока и радиусом вектором.

Примеры расчета индукции магнитных полей

Индукция магнитного поля в центре кругового проводника радиусом R с током I

.

Индукция магнитного поля бесконечно длинного прямого проводника с током

,

где I – сила тока, проходящего по проводнику; r – расстояние от проводника до рассматриваемой точки.

И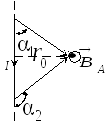ндукция магнитного поля прямого проводника конечной длины с токомI (рис. 10)

,

Рис. 10

где r₀ – кратчайшее расстояние от проводника до рассматриваемой точки поля.

Индукция магнитного поля бесконечно длинного соленоида

B = ₀ nI,

где n – число витков на единицу длины соленоида.

Индукция магнитного поля тороида (рис. 11):

1) r = r₁, В₁ = 0;

2) r = r₂, ;

3) r = r₃, В₃ = 0,

Рис. 11

где n – число витков на единицу длины средней линии тороида ();R₁ и R₂ – внутренний и внешний радиусы тороида соответственно.

Силы в магнитном поле

Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током:

а) в векторной форме ;

б) в скалярной форме ,

где – элемент тока;– вектор магнитной индукции поля, – угол между векторами элемента тока и индукцией магнитного поля.

Сила Лоренца – сила, действующая на движущийся заряд со стороны электрического и магнитного полей

,

где q – движущийся заряд; – вектор скорости заряда;– вектор напряжённости электрического поля;– вектор магнитной индукции.

«Магнитная» составляющая силы Лоренца определяется:

а) в векторной форме ;

б) в скалярной форме ,

где  – угол между векторами скорости заряда и магнитной индукции поля.

Движение точечного заряда в однородном магнитном поле.

• При  = 0 «магнитная» составляющая силы Лоренца равна нулю. Движение точечного заряда равномерное, траектория – прямая линия.

• При  = /2 «магнитная» составляющая силы Лоренца 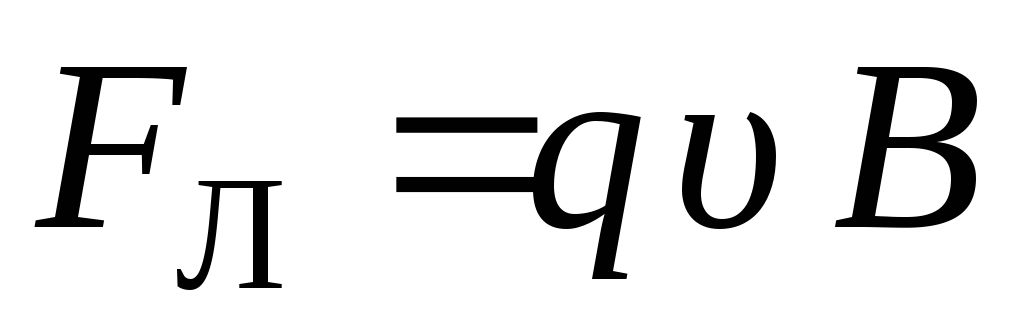. Движение точечного заряда равномерное, траектория – окружность.

• При 0 <  < /2 движение точечного заряда равномерное, траектория – винтовая линия.

Контур с током в магнитном поле

Магнитный момент контура с током

или p_m = I S,

где – вектор единичной нормали к контуру;– модуль вектора магнитного момента контура с током;I – сила тока, проходящего по контуру; S – площадь контура.

Механический момент, действующий на контур с током со стороны однородного магнитного поля:

или ,

где В – индукция магнитного поля, в котором находится контур;  – угол между вектором магнитной индукции и нормалью к контуру.

Потенциальная энергия контура с током в магнитном поле

W_п = – p_m B = –.

Электромагнитная индукция

Магнитный поток

или ,

где В – индукция магнитного поля, в котором находится контур;  – угол между вектором магнитной индукции и нормалью к контуру;S – площадь поверхности, ограниченной рассматриваемым контуром (рис. 12).

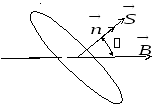
Рис. 12

Явление электромагнитной индукции заключается в том, что всякий раз при изменении магнитного потока, пронизывающего контур неподвижного или движущегося проводника, в нём возникает ЭДС индукции. Если рассматриваемый проводник замкнутый, то в нем возникает индукционный ток.

ЭДС индукции и индукционный ток:

, .

Если контур состоит из N витков, ЭДС индукции определяется уравнением

,

где  = N – потокосцепление.

Явление самоиндукции является частным случаем электромагнитной индукции. Оно возникает в проводящей электрический ток среде при изменении силы тока в ней или параметров среды. Так как  = LI, то ЭДС самоиндукции определяется уравнением

Если L = const, то

,

где L – индуктивность проводящей среды (проводника).

Индуктивность можно рассматривать как коэффициент пропорциональности между магнитным потоком и силой тока, создающего магнитное поле. Она зависит от формы и размеров проводника, а также от его магнитных параметров и магнитных характеристик окружающей среды. Индуктивность бесконечно длинного соленоида определяется уравнением

L =  ₀ nV,

где n – число витков, приходящихся на единицу длины соленоида; V – объём соленоида;  – магнитная проницаемость сердечника соленоида.

Энергия магнитного поля

.

Объёмная плотность энергии для магнитного поля

.