5семанглийскоеКалинина / третийкурс / величина / величинакалинина5

Между тем вычисления должны быть на чем-то основаны, если не на определении, то на каких-то принципах, которые позволяли бы всякий раз получать значение площади - определенное число. Эти принципы существовали давно, хотя долго не формулировались. Эти принципы - основные свойства площади:

() - площадь фигуры есть неотрицательное число;

() - площадь фигуры, составленной из нескольких фигур без общих внутренних точек, равна сумме площадей этих фигур;

() - равные фигуры имеют равные площади;

() - площадь единичного квадрата равна единице.

Свойство () называется положительностью , свойство () аддитивностью, () называется инвариантностью, а свойство () - нормированностью.

Под единичным квадратом понимается квадрат, построенный на единичном отрезке.

Речь идет исключительно о плоских фигурах.

Эти свойства не были единственными, которыми математики пользовались при вычислении площадей. Но все иные свойства являются следствиями этих четырех свойств. Так, например, легко доказать, что площадь части фигуры не превышает площади всей фигуры. Это свойство называют монотонностью площади.

Действительно, пусть фигура G является внутренней частью фигуры F. Тогда фигура G дополняет фигуру G до фигуры F. Фигуры G и G вместе составляют фигуру F (рис.6). Так как они не имеют общих внутренних точек, то по свойству ():

площадь F = площадь G + площадь G,

а так как площадь G≥ 0 (свойство ()),

то получаем, что площадь F ≥ площадь G.

Рис.6

Сначала математики научились вычислять площади многоугольных фигур, т.е. фигур, которые ограничены конечным числом отрезков прямых. Было установлено, что площадь треугольника равна половине произведения основания на высоту. Для вычисления площади произвольной многоугольной фигуры достаточно разбить ее на треугольники без общих внутренних точек и, найдя площади этих треугольников, сложить полученные результаты.

Переходя к фигурам, ограниченным кривыми линиями, математики стали их "приближать" многоугольниками. Пусть фигура F -фигура, площадь которой должна быть вычислена. Но она не является многоугольной фигурой. Рассмотрим, с одной стороны, всевозможные многоугольные фигуры, содержащиеся в F, с другой стороны, - всевозможные многоугольные фигуры, содержащие F. Первые называют входящими в F, а вторые - объемлющими F (рис.7)

Рис.7

В силу монотонности площади, для любой входящей многоугольной фигуры P и любой объемлющей многоугольной фигуры Q справедливо:

площадь P≤ площадь F ≤ площадь Q

Таким образом, площади фигур P и Q служат приближенными значениями площади фигуры F с недостатком и с избытком.

Погрешности обоих приближений, т.е. разности площадей фигур F и P , а также фигур Q и F, не превышают разности площадей фигур Q и P. Предположим, что путем надлежащего выбора многоугольных фигур P и Q мы можем сделать разность их площадей сколь угодно малой. Значит, и погрешности приближений могут быть сделаны сколь угодно малыми. Тем самым площадь фигуры F может быть вычислена с произвольной степенью точности. Но этот метод применим лишь к таким фигурам F, для которых существуют входящие многоугольные фигуры P и объемлющие многоугольные фигуры Q со сколь угодно малыми разностями площадей. Такие фигуры называют квадрируемыми. Класс квадрируемых фигур очень широк. Можно доказать, что всякий многоугольник является квадрируемой фигурой.

Сразу же оговоримся, что мы будем рассматривать лишь квадрируемые фигуры, т.е. фигуры, которые можно целиком поместить внутри некоторого многоугольника и в которые можно вписать многоугольник. Причем разность площадей объемлющего и входящего многоугольников можно сделать сколь угодно малой.

Площадь может быть определена как функция квадрируемой фигуры, обладающая свойствами:

() - площадь фигуры есть неотрицательное число;

() - площадь фигуры, составленной из нескольких фигур без общих внутренних точек, равна сумме площадей этих фигур;

() - равные фигуры имеют равные площади;

() - площадь единичного квадрата равна единице.

Это определение является аксиоматическим. Роль аксиом играют свойства () - (). Но при таком определении должно быть доказано существование такой функции. Все же известные способы доказательства существования функции со свойствами () - () заключаются в прямом построении этой функции, т.е. в описании процесса, позволяющего по фигуре F найти число - площадь F. После того, как функция построена устанавливается, что она обладает свойствами () - (). Всякое прямое построение функции со свойствами () - () само, очевидно, может служить определением площади. Такое определение называют конструктивным. Если при аксиоматическом определении должно быть доказано существование и единственность функции, то при конструктивном определении подлежат доказательству свойства () - (). Более естественным является конструктивный подход к понятию "площадь фигуры", содержащийся в широко известной наивной формулировке: "площадь фигуры есть число единиц площади, заключенных в этой фигуре".

Этой формулировке можно придать точный смысл. Построим на плоскости две взаимно перпендикулярные прямые и и на каждой из них по обе стороны от точки их пересечения построим один за другим отрезки, равные отрезку, принятому за единицу измерения длины отрезков . Затем через конец каждого из построенных отрезков проведем прямые, перпендикулярные к той прямой, на которой лежит данный отрезок. При этом вся плоскость разобьется на равные квадраты со стороной, равной единице длины . Будем говорить, что на плоскости построена сеть квадратов нулевого ранга.

Аналогичным образом строится на плоскости сеть квадратов первого ранга – стороны квадратов первого ранга равны отрезку:

= .

Легко заметить, что в каждом квадрате нулевого ранга содержится квадратов первого ранга. Точно так же можно построить сеть квадратов второго ранга со стороной:

=

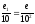
В каждом квадрате первого ранга содержится квадратов второго ранга, а в каждом квадрате нулевого ранга квадратов второго ранга.

Аналогичным образом строится на плоскости сеть квадратов го ранга при любом натуральном . Теперь будем говорить, что на плоскости построены сети квадратов на отрезке .

Представление о сетях квадратов на плоскости можно получить, рассматривая миллиметровую бумагу: на ней можно увидеть сеть квадратов первого ранга, построенную на отрезке 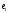=1 дм, а также сети второго и третьего рангов. Построить сеть четвертого и последующего рангов уже не представляется возможным из-за малых размеров квадратов, их составляющих.

Пусть фигура расположена на плоскости, на которой построены сети квадратов на единичном отрезке (рис.8).

1. Подсчитаем, сколько квадратов первого ранга лежат внутри фигуры , т.е. состоят только из точек фигуры F. Обозначим число этих квадратов буквой . (Понятно, что ни один квадратный дециметр не умещается внутри фигуры, изображенной на рисунке. Таким образом, =0).

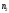Подсчитаем теперь, сколько квадратов второго ранга всеми своими точками лежат внутри фигуры . Это число обозначим буквой . (на рис. их число = 27. Это квадратные сантиметры.)

Подсчитаем теперь, сколько квадратов третьего ранга всеми своими точками лежат внутри фигуры . Это число обозначим . (Понятно, что наши глаза не позволяют подсчитать число квадратных миллиметров, целиком лежащих внутри фигуры , хотя еще различают их.) Заметим, что, в общем случае число квадратов третьего ранга, лежащих внутри фигуры больше,так как, кроме тех квадратов третьего ранга, которые находятся внутри квадратов второго ранга, еще некоторые квадраты третьего ранга лежат внутри фигуры . Можно доказать, что .

Идеализируя указанный процесс, можно говорить о числе квадратов -го ранга, лежащих внутри фигуры , при любых натуральных значениях , т.е. мыслить указанный процесс нахождения чисел – бесконечным. Конечно, на практике этот процесс не бесконечен. Это объясняется ограниченными возможностями нашего инструментария.

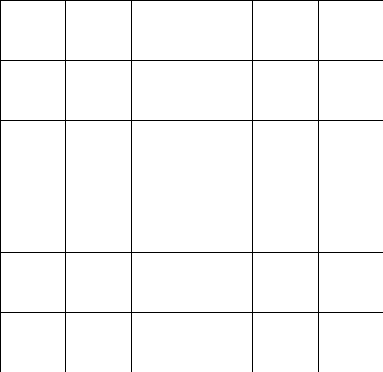
Рис.8

Рассмотрим следующую бесконечную последовательность:

; ; ;...; ;...(1) Эта последовательность является неубывающей. В самом деле:

так как ;

;так как ; и т.д. Эта же последовательность ограничена сверху. Докажем это. Обозначим число квадратов нулевого ранга, задевающих фигуру , т.е. имеющих с ней хотя бы одну общую внутреннюю точку, через (в соответствии с рисунком это число равно 1, так как вся фигура лежит внутри единичного квадрата - квадратного метра).

Очевидно, что при любом натуральном значении все 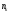квадратов -го ранга, лежащие внутри фигуры , лежат также и внутри тех квадратов -го ранга, которые “задевают” фигуру . А так как внутри каждого квадрата нулевого ранга содержится квадратов -го ранга, то , т.е. для всех натуральных значений . Это и означает, что последовательность (1) ограничена сверху числом .

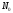Итак, последовательность (1) является неубывающей и ограниченной сверху. Отсюда следует, что эта последовательность имеет предел. Так как

6