5семанглийскоеКалинина / третийкурс / величина / величинакалинина2

Понятие величины.

Понятие величины является одним из основных понятий, применяемых не только в математике, но и в физике, химии, других науках. Термин “величина” часто используется некорректно. Причины такого положения связаны с тем, что, во-первых, понятие величины не является специфическим математическим понятием и используется во многих науках в разных смыслах, и, во-вторых, путь введения этого понятия еще не получил достаточно четкого освещения в методической науке.

Впервые понятие величины возникло в философской литературе. Древнегреческий философ Аристотель писал: “То или иное количество есть множество, если его счесть; есть величина, если его можно измерить”. Это еще не определение, но уже попытка провести грань между числом и величиной, между натуральными и действительными числами.

В книге Евклида “Начала” нет понятия величины, но в ней перечисляются аксиомы, описывающие общие свойства величин: равные одному и тому же равны между собой; если к равным прибавить равные, то целые будут равны между собой; целое больше своей части и пр.

В математической литературе часто давались описательные определения величины. Так Герон Александрийский писал:

“Величина есть все то, что может быть увеличено или разделено безгранично”.

Леонард Эйлер давал такое определение: “Величина есть все то, что способно увеличиваться и уменьшаться”.

Герман Грассман писал: “Величина есть всякая вещь, которая может быть признана равной или неравной другой вещи”.

Об этих и подобных им других “определениях” французский математик Анри Лебег (1875-1941) писал: “Предполагается таким образом создать теорию, которая была бы приложима одновременно к объемам и честолюбию, к температуре и к аппетиту, к государственному бюджету и к плодородию почвы, к уму, к уровню воды в Сене, к удивлению, к образованию и т. д. … Можно сказать, что истинные затруднения представит задача отыскания чего-либо, что не является величиной….” ( См. А.Лебег “Об измерении величин” Изд-е 2-е. Госуд. Уч.пед. изд-во. –М., 1960, стр. 151-152).

Величины являются составной часть многих наук, без этого понятия они ограничивались бы лишь наблюдениями и оставались на описательном уровне. Условия для введения той или иной величины созревают в процессе развития данной области знаний, создаются постепенной работой по уточнению и дифференциации понятий опытной науки. Именно величины позволяют перейти от описательного к количественному изучению свойств объектов, т.е. математизировать знания в различных областях.

Каждый объект имеет много различных свойств, которые отражаются в соответствующих величинах. Так, свойству инертности соответствует величина, называемая массой. Свойству пространственной протяженности соответствует длина. Свойству проводника препятствовать прохождению электрического тока – сопротивление.

Величины, выражающие одно и то же свойство объектов или явлений, называются однородными. Разнородные величины выражают различные свойства.

Величины не существуют сами по себе, как некие субстанции, оторванные от материальных объектов и их свойств. В то же время, величины в некоторой степени идеализируют свойства объектов и явлений. Величины не сама реальность, а лишь ее отображение. Практика показывает, что величины верно отражают свойства окружающей действительности. По мере накопления знаний об общих свойствах конкретных величин стали возможны некоторые обобщения и систематизация этих свойств на все более высоком уровне, уровне определения общего понятия величины. В процессе длительной эволюции понятие величины уточнялось, развивалось и обобщалось, что привело в дальнейшем к понятиям скалярной, векторной и др. величин.

Мы ограничимся рассмотрением скалярных величин, т.е. величин, характеризуемых только числовым значением. В математике существует несколько подходов к определению понятия скалярной величины.

При аксиоматическом подходе, который получил широкое распространение, скалярная величина определяется косвенно через ту или иную систему аксиом. Выбор системы аксиом может быть различным. В одном случае аксиоматика скалярных величин предполагает известными действительные числа (см. определение Н.Я. Виленкина), в другом скалярная величина имеет самостоятельное определение (см. определение А.Н. Колмогорова).

Рассмотрим определение Наума Яковлевича Виленкина:

Опр.1. Множество 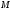называется областью определения величины, если в нем определены два отношения: бинарное отношение эквивалентности (рефлексивное, симметричное, транзитивное отношение) и тернарное отношение , элемент составлен из элементов и , причем выполняются следующие условия:

• существует хотя бы одно отображение множества в множество , такое что из следует 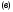, а из следует +;

• если другое отображение в с указанными свойствами, то существует такое положительное число , что для всех выполняется равенство .

Отображение в с указанными выше свойствами называют измерением величины, а число - значением величины для элемента , мерой .

В множестве задано отношение " и имеют равные меры" - отношение рановеликости. Из следует равновеликость и .

Опр.2 Величиной, заданной отношениями и в множестве называется разбиение этого множества на классы эквивалентности по отношению " равновелико ".

Рассмотрим аксиоматику Андрея Николаевича Колмогорова, которая использует лишь понятие натурального числа, и хотя и довольно объемна, но вполне доступна пониманию, за небольшим исключением, младшего школьника.

Определим класс или систему аддитивных скалярных величин.

Пусть имеется множество А элементов или объектов любой природы и на этом множестве заданы бинарные отношения равенства (=), меньше (<)[больше (>)],и операция сложения (+).

Множество А, рассматриваемое вместе с определенными на нем отношениями (=), (<) и операцией (+), называется системой однородных положительных скалярных величин, а его элементы – однородными положительными скалярными величинами, если выполняются следующие аксиомы:

1. Для любых двух а и в О А имеет место одно из трех: а = в, а > в, а < в.

2. Для любых трех а, в и с из А выполняется: если а < в и в < с, то а < с (транзитивность отношения меньше).

3. Для любых двух а и в О А существует однозначно определенная сумма с = а + в.

4. Для любых двух а и в О А выполняется а + в = в + а (коммутативность сложения).

5. Для любых трех а, в и с из А выполняется:

6. а + (в + с )= (а + в)+ с (ассоциативность сложения).

7. Для любых двух а и в О А имеет место а + в > а (монотонность сложения).

8. Для любых двух а и в О А, если а > в , то существует элемент сО А, для которого в + с = а (возможность вычитания).

9. Каков бы ни был элемент аО А и натуральное число n, найдется в О А, что n · в = а (возможность деления).

10. Для любых двух а и в О А найдется такое натуральное число n, что n · в > а (аксиома Архимеда или Евдокса). Пусть последовательность величин аi О А, где i = 1,2,3,4,…, n,… обладает свойством : а1< а2 < а3 <а4 <а5<…, а последовательность вi О А, где i = 1,2,3,4,…, n,… обладает свойством : в1> в2 > в3 > в4 > в5>…, при этом аi < вj для любых i и j О N.

Пусть для любого Ɛ>0 найдется N Ɛ , что при всех n> N Ɛ разность < Ɛ. Тогда существует единственный элемент сО А, удовлетворяющий условиям аi < с; с < вj для любых i и j О N (аксиома непрерывности).

К числу аддитивных скалярных непрерывных величин относятся длина, площадь, объем, масса. Легко проверить свойства длины отрезка. Для этого следует в формулировках общих свойств термин объект заменить на термин длина отрезка.

А вот такая величина как температура не обладает свойством аддитивности. Попробуем слить воду из двух стаканов в один, если температура воды в одном 30, а в другом 70. Вода не закипит. Ее температура не будет равной 100.

Величины тесно связаны с понятием измерения. Измерения – один из путей познания природы человеком, объединяющий теорию с практической деятельностью человека.

Измерение величин в техническом отношении носит совершенно различный характер, для длин он один, для масс - другой, для времени – третий. Однако в основе любого измерения лежит один и тот же принцип: измеряемый объект сравнивается с эталоном, т.е. предметом или явлением, величина которого принята за единицу измерения. Результат измерения выражается числом.

Если в системе аксиом 1-10 выбрать какой-либо объект за единицу измерения - , то все остальные объекты однозначно представляются в виде . Здесь - положительное действительное число, называемое мерой величины или числовым значением величины.

Итак, процесс измерения величин заключается в следующем: прежде всего из данного множества величин выбирают некоторый определенный элемент, который называется единицей измерения. Далее осуществляют операцию измерения, позволяющую при выбранной единице отнести к каждому элементу данного множества действительное число – меру этой величины, ее числовое значение.

Мера должна удовлетворять, как выяснилось в процессе длительной практической деятельности человека, таким условиям: αβγδ

(α) – мера должна быть неотрицательным действительным числом;

(β)- сумме двух элементов соответствует сумма их мер;

(γ)– равным элементам множества соответствуют равные меры;

(δ) – существует элемент, мера которого равна 1.

Возможность измерять позволяет свести сравнение величин к сравнению соответствующих им чисел, а операции над величинами к соответствующим операциям над числами. При этом, говоря о величинах, необходимо четко различать:

1. Объект или явление, к которому относится величина;

2. Саму величину, как свойство объекта или явления;

3. Числовое значение величины.

В обыденной речи такая четкость не всегда соблюдается. Понятия “величина” и “числовое значение величины” часто отождествляются, что нередко приводит к путанице и затрудняет усвоение.

Следует отметить, что множество положительных действительных чисел с определенным на нем отношение “меньше” и операцией сложения само образует систему однородных положительных скалярных величин, поскольку подчиняется аксиоматике, рассмотренной выше. Все свойства, определенные во множестве однородных положительных скалярных величин, выполняются во множестве положительных действительных чисел. Однако обратное утверждение неверно. Так, например, операция умножения скалярных величин не определена.

В школьном курсе математики аксиоматика скалярных величин полностью не раскрывается, понятием скалярной величины пользуются без определения. Однако в практике школьного преподавания используются общие сведения о скалярных величинах:

1. Скалярная величина – элемент множества однородных скалярных величин.

2. Скалярные величины могут быть разных родов.

3. Для скалярных величин одного рода вводится операция сложения и отношение порядка.

4. Скалярная величина имеет числовое значение при выбранной единице измерения. Числовое значение получают в процессе измерения.

5. При измерениях осуществляется взаимно однозначное отображение множества величин на множество неотрицательных действительных чисел при выбранной единице измерения.

6. В процессе измерений выявляются следующие свойства величин: а) равным величинам соответствуют равные числовые значения величин при одной и той же единице измерения; б) числовое значение суммы величин при одной и той же единице измерения равно сумме числовых значений слагаемых величин.

7. Запись числового значения величины осуществляется с указанием единицы измерения.

8. Для разнородных величин операция сложения и отношение порядка не определены.

Проблема изучения скалярных величин, измерений скалярных величин в школьном обучении требует рассмотрения двух моментов:

• Формирование и развитие общего формально-логического представления у учащихся о скалярной величине.

• Обучение учащихся практическому применению понятия величины в связи с измерениями и вычислениями.

При этом важно иметь в виду:

• Определение процесса измерения. Смысл этого процесса. Соотношение понятий величины и измерения.

• Единицы измерения величин. Перевод единиц.

• Методы измерений (прямой и косвенный).

• Устройство и принцип действия измерительных приборов.

• Общие правила выполнения измерений. Снятие показаний приборов.

• Формулы для косвенного измерения величин.

• Свойства величин, раскрывающиеся в процессе измерений.

• Приближенный характер измерений. Виды погрешностей. Обработка и запись результатов измерений. Пути повышения точности измерений.

Единую трактовку некоторых метрологических понятий: эталон, мера и др.

Длина отрезка

Длина является весьма сложно определяемым математическим понятием. Наиболее просто определяется длина прямолинейного отрезка. Длина может быть определена как функция отрезка, обладающая свойствами ()-():

()- длина отрезка является неотрицательным числом;

()- длина отрезка, составленного из конечного числа последовательно примыкающих друг к другу отрезков, равна сумме длин составляющих отрезков;

()- равные отрезки имеют равные длины;

()- длина единичного отрезка равна единице.

Свойства ()-() играют роль аксиом. Такое определение длины называют аксиоматическим. При таком определении требуется доказать, что крайней мере одна такая функция существует. Но все известные способы доказательства существования функции со свойствами ()-() заключаются в прямом построении этой функции, т.е. в описании процесса, позволяющего по отрезку найти число – длину отрезка. После того, как функция построена, устанавливается, что она обладает свойствами ()-(). Всякое же прямое построение функции со свойствами ()-() само может служить определением длины. Такое определение называют конструктивным определение длины отрезка. Если при аксиоматическом определении должны быть доказаны существование и единственность длины, то при конструктивном определении становятся теоремами и подлежат доказательству свойства ()-(). С логической точки зрения эти определения эквивалентны и отличаются лишь порядком изложения.