
5семанглийскоеКалинина / третийкурс / величина / величинакалинина3
.rtf
Покажем,
что свойства ()-()
однозначно определяют длину отрезка,
т.е. докажем, что существует одна и только
одна функция
 ( называемая длиной), определенная на
классе всех прямолинейных отрезков и
удовлетворяющая условиям - свойствам
()-().
( называемая длиной), определенная на
классе всех прямолинейных отрезков и
удовлетворяющая условиям - свойствам
()-().
Доказательство существования.
Возьмем
прямую
 ,
на которой расположен единичный отрезок
,
на которой расположен единичный отрезок
 .
Будем считать ее горизонтальной.
Обозначим через
.
Будем считать ее горизонтальной.
Обозначим через
 один из концов единичного отрезка.
Далее, разбив единичный отрезок на
один из концов единичного отрезка.
Далее, разбив единичный отрезок на
 ,
,
 ,
,
 ,
…,
,
…,
 равных частей и взяв одну из этих частей,
будем последовательно откладывать
вправо и влево от точки
равных частей и взяв одну из этих частей,
будем последовательно откладывать
вправо и влево от точки
 отрезки, равные этой части. В результате
вся прямая
отрезки, равные этой части. В результате
вся прямая
 будет разбита на равные отрезки, которые
мы назовем отрезками ранга
будет разбита на равные отрезки, которые
мы назовем отрезками ранга
 .
.
Примером
такого разбиения может служить
миллиметровка. Единичный отрезок –
отрезок, равный 1 м, отрезки первого
ранга – дециметры, отрезки второго
ранга – сантиметры, третьего – миллиметры.
Более мелкие отрезки не видны глазу,
однако теоретически разбиение прямой
на отрезки ранга
 можно продолжать бесконечно. Заметим,
что
можно продолжать бесконечно. Заметим,
что
 - натуральное число, показывающее степень
числа 10. Единичный отрезок разбит при
этом на
- натуральное число, показывающее степень
числа 10. Единичный отрезок разбит при
этом на
 равных частей.
равных частей.
Пусть
теперь
 - произвольный отрезок, расположенный
на прямой
- произвольный отрезок, расположенный
на прямой
 .
Обозначим через
.
Обозначим через
 число отрезков ранга
число отрезков ранга
 ,
целиком содержащихся в отрезке
,
целиком содержащихся в отрезке
 .
.
Параллельно
теоретическим рассуждениям будем вести
практическую работу на модели прямой
 и отрезка
и отрезка
 .
(рис.1)
.
(рис.1)





рис.1
На
модели подсчитаем число отрезков
первого, второго и третьего ранга,
целиком лежащих в отрезке
 .
Видим, что
.
Видим, что
 = 1 (внутри отрезка уместился 1 дм - рис.1),
= 1 (внутри отрезка уместился 1 дм - рис.1),
 = 10 (внутри отрезка уместились целиком
10 см- рис.1),
= 10 (внутри отрезка уместились целиком
10 см- рис.1),
 = 108 (внутри отрезка уместились целиком
108 мм-- рис.2 и рис.3). Последний результат
может быть и другим, ошибка в 1-2 мм вполне
допустима.
= 108 (внутри отрезка уместились целиком
108 мм-- рис.2 и рис.3). Последний результат
может быть и другим, ошибка в 1-2 мм вполне
допустима.
Теперь
подсчитаем число отрезков ранга
 ,
имеющих с данным отрезком
,
имеющих с данным отрезком
 хотя бы одну общую точку. Обозначим это
число
хотя бы одну общую точку. Обозначим это
число
 .
.





Рис.2





Рис.3
Вновь
обратимся к модели. Видим, что
 = 3,
= 3,
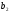 = 12,
= 12,
 = 110. Ясно, что если мы возьмем самый
“правый” из содержащихся в
= 110. Ясно, что если мы возьмем самый
“правый” из содержащихся в
 отрезков ранга
отрезков ранга
 ,
то примыкающий к нему справа отрезок
ранга
,
то примыкающий к нему справа отрезок
ранга
 имеет с отрезком
имеет с отрезком
 общие точки, но не содержится целиком
в отрезке
общие точки, но не содержится целиком
в отрезке
 .
Аналогично, для самого “левого” из
содержащихся в отрезке
.
Аналогично, для самого “левого” из
содержащихся в отрезке
 отрезков ранга
отрезков ранга
 .
Следовательно: (
.
Следовательно: ( -
-
 )=
2. Проверим, что разности (
)=
2. Проверим, что разности ( -
-
 ),
(
),
(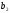 -
-
 ),
(
),
( -
-
 )
имеют значение, равное 2. Значение
разности (
)
имеют значение, равное 2. Значение
разности ( -
-
 )
может быть и меньше 2. Если один из концов
отрезка
)
может быть и меньше 2. Если один из концов
отрезка
 совпадет с концом отрезка ранга
совпадет с концом отрезка ранга
 ,
то эта разность будет равна 1, если же
оба конца отрезка
,
то эта разность будет равна 1, если же
оба конца отрезка
 совпадут с концами отрезков ранга
совпадут с концами отрезков ранга
 ,
то разность будет равна 0.
,
то разность будет равна 0.
Положим
 =
=
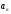
 ;
;
 =
=

 .
Числа
.
Числа
 и
и
 определены для любого
определены для любого
 .
Легко видеть, что имеют место соотношения
:
.
Легко видеть, что имеют место соотношения
:
 (
(
 =0,1
;
=0,1
;
 =0,10
;
=0,10
;
 =0,108
);
=0,108
);
 (
(
 =0,3
;
=0,3
;
 =0,12
;
=0,12
;
 =0,110
).
=0,110
).
Действительно,
всякий отрезок ранга
 разбит на 10 отрезков ранга
разбит на 10 отрезков ранга
 +1.
Если исходный отрезок ранга
+1.
Если исходный отрезок ранга
 содержится в отрезке
содержится в отрезке
 ,
то каждый из десяти отрезков ранга
,
то каждый из десяти отрезков ранга
 +1
содержится в
+1
содержится в
 .
.
Если
хотя бы один из десяти отрезков ранга
 +1
имеет общую точку с отрезком
+1
имеет общую точку с отрезком
 ,
то и исходный отрезок ранга
,
то и исходный отрезок ранга
 имеет общую точку с отрезком
имеет общую точку с отрезком
 .
Отсюда
.
Отсюда
 и
и
 ,
а потому
,
а потому
 ;
;
 .
.
Из
очевидного соотношения
 (
( )
находим, что монотонная последовательность
)
находим, что монотонная последовательность
 ;
;
 ;
;
 …
ограничена сверху для любого
…
ограничена сверху для любого
 :
:


 .
Следовательно, существует предел
.
Следовательно, существует предел

 .Так
как всякая
.Так
как всякая
