5семанглийскоеКалинина / третийкурс / величина / Величинакалинина4
.rtf
Точно
так же для отрезка
,
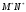образованного всеми
отрезками ранга
,
имеющими с отрезком
общие точки, найдем
.
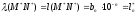Замечание.
Из свойств ()
и ()
вытекает монотонность функци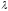й
и
.
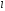То есть, если отрезок
часть отрезка
,
то
и
.
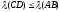Так
как отрезок
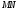содержится в отрезке
,
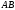то:
;
.
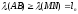Аналогично, имеем:
;
.
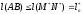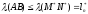Отсюда получаем, что:
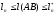и
.
Модуль
разности функций для отрезка
удовлетворяет неравенству:
,
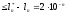в силу произвольности
получаем:
.
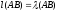Итак,
для отрезка
,
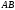расположенного на прямой
,
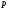функции
и
принимают одно и то же значение. Из
свойства ()
получаем, что функции
и
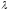совпадают.
Замечание. В проведенных доказательствах существенно была использована аксиома Архимеда (9 аксиома в определении величины). Единичный отрезок разбивался на равные отрезки.
С
процессом измерения тесно связана и
аксиома непрерывности или аксиома
Кантора (10 аксиома в определении общего
понятия величины). Для любого числа
>
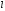0 существует отрезок, длина которого
равна
.
Площадь плоской фигуры.
Площадь принадлежит к числу наиболее широко известных математических понятий. Понятие “площадь фигуры” возникло на основе рассмотрения задач практического содержания таких типов: “Сколько зерна нужно иметь для засева данного поля?”, “Сколько плиток паркета нужно для того, чтобы уложить пол в помещении?” и др. Менее известен тот факт, что площадь очень непростое понятие. Точное определение площади представляет значительные логические трудности. Многим понятие "площадь" кажется первичным, не подлежащим определению понятием. Такой взгляд на это понятие сложился еще в древности. На протяжении многих столетий главное видели не в определении понятия "площадь", а в вычислении площадей.