
- •Саратовский государственный технический университет
- •Лабораторная работа 1 определение коэффициента взаимной диффузии воздуха и водяного пара
- •Основные теоретические положения
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Обработка результатов измерений
- •Лабораторная работа 2 определение коэффициента теплопроводности методом нагретой нити
- •Основные теоретические положения
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Обработка результатов измерений
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Обработка результатов эксперимента
- •Лабораторная работа 4 Определение отношения теплоемкостей воздуха при постоянных давлении и объеме
- •Основные теоретические сведения
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Обработка результатов измерений
Описание экспериментальной установки и порядок выполнения работы
Для проведения измерений предназначена установка, представленная на рис. 2.3.
Температура воздуха в трубке определяется цифровым термометром. Значения падения напряжений на эталонном резисторе и на нити измеряются цифровым вольтметром.
Температура нити и, следовательно, значения напряжения на нити меняется с помощью регулятора «Нагрев».
Геометрические размеры рабочего элемента (радиус трубки, радиус нити, высота трубки), сопротивление эталонного резистора и температурный коэффициент нити указаны на стенде со справочными данными в лаборатории.
 Рис.
2.3. Экспериментальная установка для
определения
Рис.
2.3. Экспериментальная установка для
определения
коэффициента теплопроводности воздуха.
Эксперимент осуществляется в следующей последовательности.
Включить установку тумблером «Сеть». Включить тумблер «Нагрев».
Нажать кнопку
 (режим измерения падения напряжения
на эталонном резисторе) и установить
регулятором «Нагрев» падение напряжения
не более 0,06 В. При этом температура
проволоки остается практически
неизменной (ненагревающий ток). Измерить
при помощи индикатора2напряжение
на резисторе
(режим измерения падения напряжения
на эталонном резисторе) и установить
регулятором «Нагрев» падение напряжения
не более 0,06 В. При этом температура
проволоки остается практически
неизменной (ненагревающий ток). Измерить
при помощи индикатора2напряжение
на резисторе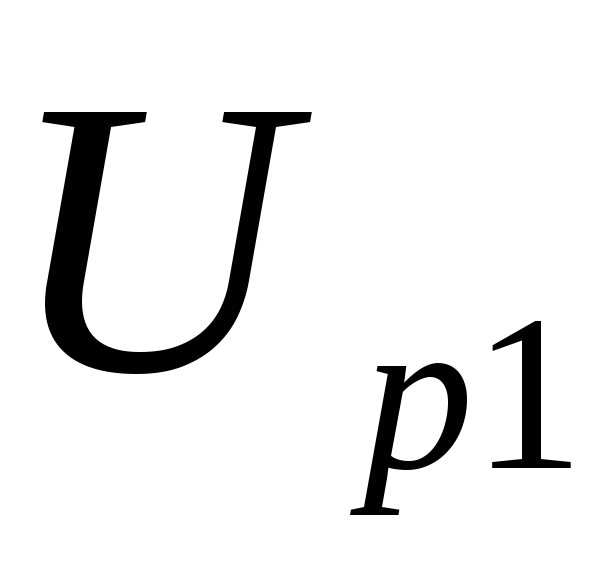 и записать его значение в таблицу.
и записать его значение в таблицу.Нажать кнопку
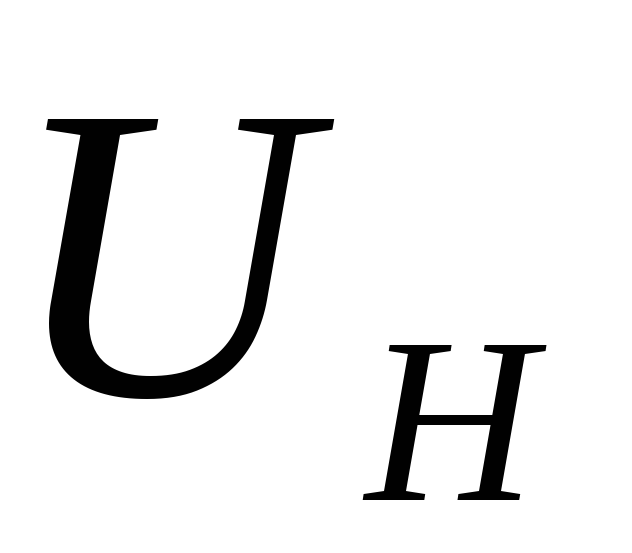 и записать показания индикатора2
и записать показания индикатора2 .
.Повторить измерения п.п. 2,3 для нескольких значений напряжения
 .
Все результаты занести в таблицу.
.
Все результаты занести в таблицу.Нажать кнопку
 ,
и с помощью регулятора «Нагрев»
установить падение напряжения на
эталонном резисторе
,
и с помощью регулятора «Нагрев»
установить падение напряжения на
эталонном резисторе в диапазоне 0,3-1,5 мВ.
в диапазоне 0,3-1,5 мВ.Подождав 2 минуты, что необходимо для стабилизации теплового режима рабочего элемента, нажать кнопку
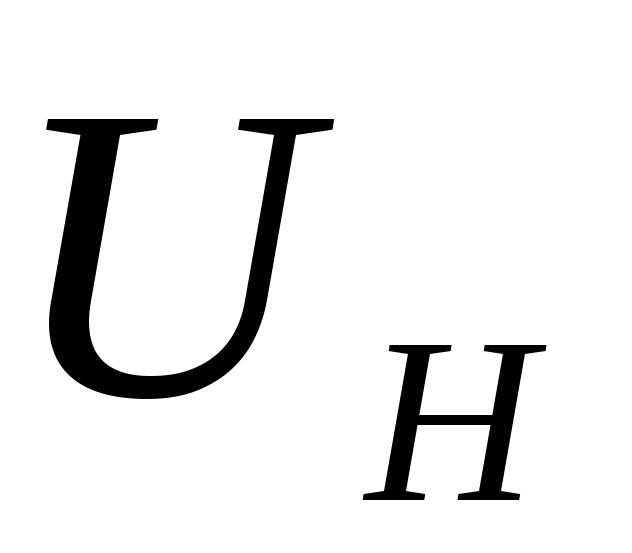 и определить падение напряжения на
нити
и определить падение напряжения на
нити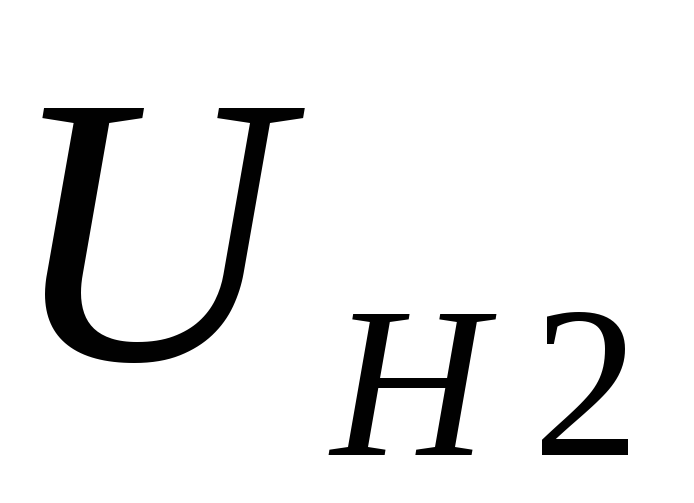 .
.Повторить измерения п.п. 5 и 6 для нескольких значений падения напряжения
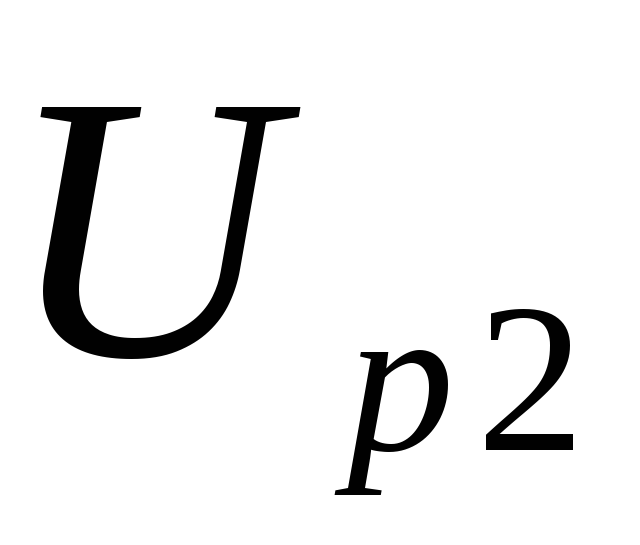 .
Результаты измерений записать в таблицу.
.
Результаты измерений записать в таблицу.После измерений вывести ручку «Нагрев» на минимум; отключить тумблер «Нагрев»; выключить установку.
По формуле (2.24) рассчитать значения коэффициента теплопроводности
 .
.
Обработка результатов измерений
По формуле (П.1) определить среднее
значение коэффициента теплопроводности
воздуха
![]() .
Рассчитать величину абсолютной
погрешности коэффициента теплопроводности
по формуле (П 3).
.
Рассчитать величину абсолютной
погрешности коэффициента теплопроводности
по формуле (П 3).
Лабораторная работа 3
ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ ПЛАВЛЕНИИ
И НАГРЕВАНИИ ОЛОВА
Цель работы: ознакомиться с первым и вторым началами термодинамики, понятием энтропии; экспериментально определить температуру плавления олова и рассчитать изменение энтропии олова при его нагревании и плавлении.
Основные теоретические сведения
Основными величинами, которыми оперирует термодинамика, являются внутренняя энергия термодинамической системы U, теплотаQ, переданная ей,и совершенная системой работаA.
Внутренняя энергия телаUпредставляет собой полную энергию беспорядочного движения молекул ( поступательного, колебательного и вращательного ).
При взаимодействии термодинамической системы с окружающими телами происходит обмен энергией. При этом возможны два различных способа передачи энергии от системы к внешним телам: с изменением внешних параметров системы и без изменения этих параметров. Первый способ передачи энергии называется работой, второй – теплотой.
Теплота, работа и внутренняя энергия связаны между собой соотношением:
![]() . (3.1)
. (3.1)
Соотношение (3.1) представляет собой Iначало термодинамики:количество
теплоты
![]() ,
переданное системе, идёт на увеличение
её
,
переданное системе, идёт на увеличение
её
внутренней энергии
![]() и на работу
и на работу![]() ,
совершаемую силами, приложенными со
стороны системы к внешним телам.
,
совершаемую силами, приложенными со
стороны системы к внешним телам.
Из определения внутренней энергии
следует, что в любом состоянии системы
она имеет определённое значение, которое
не зависит от того, каким способом это
состояние было получено. Внутренняя
энергия
![]() являетсяфункцией состояниятермодинамической системы. Если система
совершает круговой (циклический) процесс,
то полное изменение её внутренней
энергии
являетсяфункцией состояниятермодинамической системы. Если система
совершает круговой (циклический) процесс,
то полное изменение её внутренней
энергии![]() .
Математически это означает, что
подинтегральное выражение
.
Математически это означает, что
подинтегральное выражение![]()
![]() является полным дифференциалом
некоторой функции.
является полным дифференциалом
некоторой функции.
Работа
![]() , совершаемая в круговом процессе, во
всех случаях, когда имеет место нагревание,
не равна нулю. Это означает, что работаAне является функцией
состояния системы. Работа – это функция
процесса. Следовательно, элементарная
работа
, совершаемая в круговом процессе, во
всех случаях, когда имеет место нагревание,
не равна нулю. Это означает, что работаAне является функцией
состояния системы. Работа – это функция
процесса. Следовательно, элементарная
работа
![]() в (3.1) не представляет собой полного
дифференциала. То же самое относится
к количеству теплоты: в разных
термодинамических процессах количество
теплоты, которое требуется для нагревании
системы от температурыT1до температурыT2различно. Количество теплоты не является
функцией состоянии системы, а элементарная
теплота
в (3.1) не представляет собой полного
дифференциала. То же самое относится
к количеству теплоты: в разных
термодинамических процессах количество
теплоты, которое требуется для нагревании
системы от температурыT1до температурыT2различно. Количество теплоты не является
функцией состоянии системы, а элементарная
теплота
![]() не является полным дифференциалом.
не является полным дифференциалом.
Опыт показывает, что две формы передачи энергии в форме теплоты и в форме работы не являются равноценными. При преобразовании работы в теплоту можно ограничиться только двумя телами, из которых одно передаёт при тепловом контакте энергию другому. При превращении теплоты в работу необходимо иметь по меньшей мере три тела: первое отдаёт энергию в форме теплоты (нагреватель), второе получает эту теплоту и отдаёт энергию в форме работы (рабочее тело) и третье тело, которому рабочее тело непременно отдаёт часть полученной от нагревателя теплоты (холодильник).
Такая неравноправность превращения теплоты в работу по сравнению с превращением работы в теплоту, связана с односторонностью естественных процессов.
Для рассмотрения этого свойства термодинамических процессов введём понятия квазистатического, обратимого и необратимого процессов.
Система находится в термодинамическом равновесии, если макроскопические величины, определяющие её состояние остаются постоянными и равными своим средним значениям. В случае идеального газа, например, такими макроскопическими величинами являются прежде всего давление и температура. В состоянии равновесия не могут происходить такие явления, как теплопроводность, диффузия, химические реакции, фазовые переходы.
Процессы, в ходе которых система всё время остаётся в состоянии равновесия, называются квазистатическими.
Если термодинамическая система по каким – либо причинам не находится в состоянии равновесия или выведена из него и после этого предоставлена самой себе, то, как показывает опыт, сам собой происходит переход к равновесному состоянию.
Процесс перехода к равновесию называется релаксацией, а время, требующееся на это, называетсявременем релаксации.
Реальный процесс можно считать квазистатическим, если скорость изменения какого – либо параметра системы (например, давления в газе) гораздо меньше средней скорости изменения этого параметра при релаксации.
Когда равновесие уже установилось, система не может сама собой возвратиться в первоначальное неравновесное состояние.
Так, например, если два соприкасающихся тела обладали в начале разностью температур и были предоставлены самим себе, то, в конце концов, температуры обоих тел выравниваются. Но обратный процесс – увеличение разности температур между ними – без внешнего воздействия не происходит.
Газ сам по себе всегда распределяется равномерно по всему объёму сосуда, и такое состояние соответствует равновесию. Но газ никогда не скапливается в одной части сосуда в большем количестве (с большей плотностью), чем в другой, без действия внешних сил.
Точно также, если ввести в сосуд два разных газа, то вследствие взаимной диффузии они сами собой перемешаются, так что состав смеси станет всюду одинаковым. Это и будет равновесным состоянием. Однако, чтобы разделить газы, требуется затратить большие усилия извне.
Приведённые примеры показывают, что естественные процессы идут в определённом направлении: от неравновесного состояния к равновесному. Эти процессы, происходящие в молекулярных системах, имеют важную особенность – они необратимы. Этим молекулярные процессы отличаются от чисто механических, для которых характерна строгая обратимость.
Обратимым процессом называется такое изменение состояния системы, которое, будучи проведено в обратном направлении, возвращает её в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, но в обратной последовательности, а состояние тел вне системы осталось неизменным.
Процессы, не удовлетворяющие этим условиям, являются необратимыми.
Все квазистатические процессы обратимы. Полностью необратимые процессы происходят часто. К числу таких процессов относятся расширение газа в пустоту, не уравновешенное внешними силами, теплопроводность, диффузия, внутреннее трение. Напротив, полностью необратимые процессы представляют собой идеальные предельные случаи реальных процессов. Все действительно происходящие процессы только частично обратимы; они всегда содержат необратимую часть.
Физическая величина, которая количественно характеризует направленность необратимых процессов и неравнозначность преобразования теплоты в работу и наоборот, называется энтропией.
Введём понятие энтропии на примере идеального газа. Разделим обе части равенства (3.1) на абсолютную температуру Т:
![]() . (3.2)
В случае
идеального газа
. (3.2)
В случае
идеального газа
![]() ,
(3.3)
где
,
(3.3)
где![]() – количество газа;
– количество газа;![]() – молярная теплоёмкость газа при
постоянном объёме,
– молярная теплоёмкость газа при
постоянном объёме,![]() –
изменение его температуры.
–
изменение его температуры.
Элементарная работа
![]() , (3.4)
гдер
–давление;dV –изменение объёма газа.
, (3.4)
гдер
–давление;dV –изменение объёма газа.
Из уравнения Клапейрона- Менделеева:
![]() .
(3.5)
Подставляя
(3.3)-(3.5) в уравнение (3.2), получим:
.
(3.5)
Подставляя
(3.3)-(3.5) в уравнение (3.2), получим:
![]() . (3.6)
Учитывая, что
. (3.6)
Учитывая, что![]() и
и![]() , перепишем уравнение (6) в виде
, перепишем уравнение (6) в виде
![]() .
(3.7)
.
(3.7)
Правая часть этого равенства представляет
собой полный дифференциал, следовательно,
и левая часть
![]() также есть полный
дифференциал
некоторой функцииS:
также есть полный
дифференциал
некоторой функцииS:
![]() . (3.8)
. (3.8)
Введенная таким образом функция S называется энтропией.Энтропия, также как и внутренняя энергия, является функцией состояния системы, поэтому
![]() (равенство Клаузиуса).
(3.9)
(равенство Клаузиуса).
(3.9)
Заметим, что уравнение Клапейрона-Менделеева описывает квазистатические процессы, происходящие в идеальных газах, и, следовательно, выражения (3.8) и (3.9) получены лишь для обратимых процессов в идеальных газах.
В термодинамике доказывается, что соотношения (3.8) и (3.9) можно распространить на обратимые процессы и в системах, отличных от идеального газа. При любом обратимом изменении состояния замкнутой системы энтропия системы не изменяется. Из равенств (3.1) и (3.8) имеем:
![]() . (3.10)
. (3.10)
Уравнение (3.10) называется термодинамическим тождеством или вторым началом термодинамики для обратимых процессов.
Важной особенностью энтропии является её поведение в необратимых процессах. Если круговой процесс необратим, то можно показать, что
![]() (неравенство Клаузиуса).
(3.11)
(неравенство Клаузиуса).
(3.11)
Рассмотрим процесс, при котором система необратимым образом переходит из равновесного состояния 1 в равновесное состояние 2. Необратимость перехода означает, что промежуточные состояния неравновесны. Вернём систему в исходное состояние каким – либо обратимым путем 2-1 (рис. 3.1). Получившийся круговой процесс необратим, потому что одна его часть необратима. Поэтому для него справедливо неравенство (3.11):
![]() .
(3.12)
.
(3.12)
Второй интеграл относится к обратимому процессу и равен:
![]() (3.13)
(3.13)
Следовательно
![]()
или
![]() .
.
Если система замкнута, т.е изолирована
от источников теплоты, то
![]() и
и![]() или
или
![]() . (3.14)
Отсюда
следует, чтоэнтропия замкнутой системы
при необратимом процессе возрастает.
. (3.14)
Отсюда
следует, чтоэнтропия замкнутой системы
при необратимом процессе возрастает.
Обобщая выводы о поведении энтропии в замкнутых системах (3.9) и (3.14), можно утверждать, что энтропия замкнутой системы не убывает (второе начало термодинамики).
В необратимых процессах в замкнутых системах энтропия всегда возрастает, и это свойство также присуще энтропии, как энергии свойственно сохраняться при любых процессах в замкнутых системах.
Именно потому, что энергия обладает свойством сохраняться в замкнутой системе, она не может служить функцией, показывающей, в каком направлении идут процессы в такой системе. Энтропия в естественно идущих процессах всегда возрастающая, позволяет судить, какое направление процесса возможно и какое нет, какое состояние является начальным и какое конечным.
Рост энтропии в любом процессе продолжается не беспредельно, а лишь до определенного максимального значения, характерного для данной системы. Это максимальное значение энтропии соответствует состоянию равновесия, и после того как оно достигнуто, какие бы то ни было изменения состояния без внешнего воздействия прекращаются.
Энтропия как функция состояния существенно отличается от энергии. В то время как энергия не может быть ни создана, ни уничтожена, энтропия может создаваться и она постоянно создаётся во всяком процессе перехода к равновесию. Но, однажды созданная, она уже не может быть уничтожена: обратный процесс с уменьшением энтропии не может идти.
