Матричные игры

В том случае, когда множество стратегий игроков конечно, функцию платежей можно представить в виде матрицы:

Обозначим

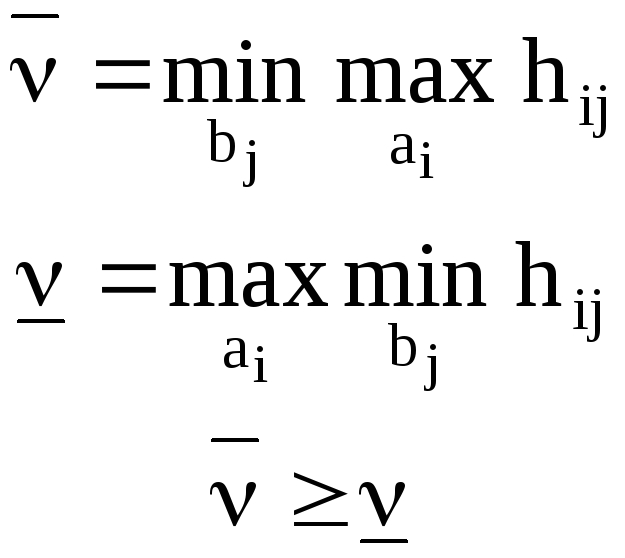
В случае существования седловой точки .

Тактика игроков

Рассмотрим тактику каждого из игроков. Будем считать, что каждый из игроков разумен.

Рассуждаем за второго игрока.

Второй игрок, минимизирующий, полагает, что при выборе любой его стратегии первый игрок стараясь получить больше, выберет в соответствующем столбце максимальный элемент, тогда второму игроку целесообразно выбрать такую стратегию, для которой этот максимум минимален. Не трудно видеть, что при таком выборе стратегии вторым игроком он не может проиграть больше чем

.

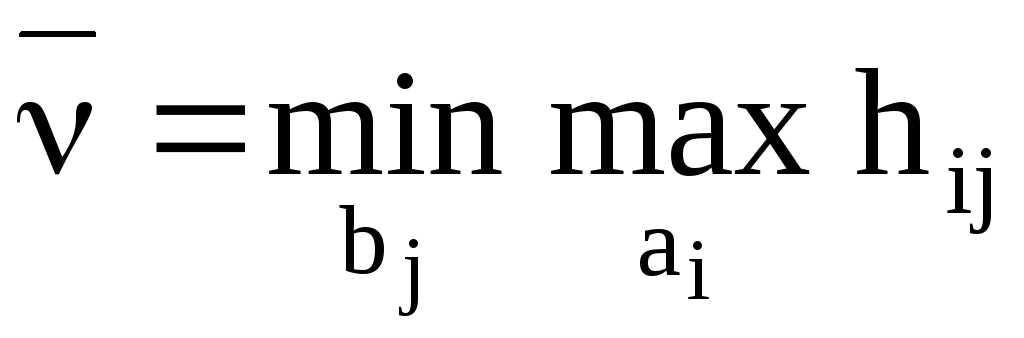Рассуждаем за первого игрока.

Если выбрать i стратегию, то мой противник выберет тот столбец, в котором есть минимальный элемент; Следовательно, первый игрок должен выбрать такую строку, в которой этот минимум максимален и тогда его выигрыш никогда не будет меньше чем .

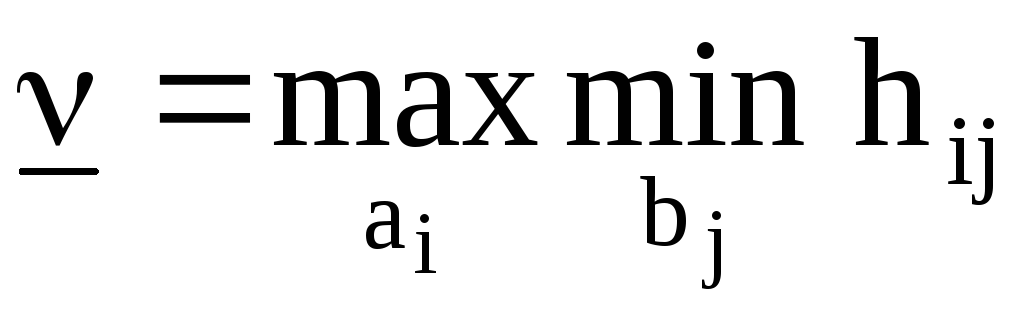Две возможные ситуации:

Если , то говорят ,что игра имеет решение вчистых стратегиях, в противном случае будем говорить, что в чистых стратегиях игра решения не имеет.

- нижняя цена игры, - цена игры,- верхняя цена игры

В случае если игра имеет решение то решением называется цена игры и пара стратегий, для которых имеет место равенство

Пример 1. (Седловая точка существует)

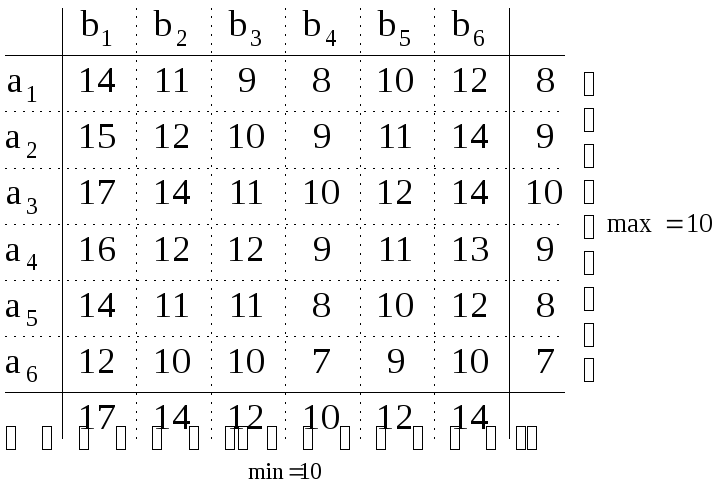
a₃ и b₄ – пара оптимальных стратегий первого и второго игрока;

10 – цена игры (седловая точка).

Пример 2. (Седловой точки нет)

i₀=3

j₀=4

Метод минимакса

В данном случае игра решения не имеет, т.к. седловой точки нет (4<6), однако при выборе «оптимальных» стратегий игроки все же обеспечили себе результат не хуже гарантированного. Каждый из игроков может выбрать одну из двух «оптимальных» стратегий ( первый игрок -2 и 3, второй игрок – 2 и 4).

Рассмотрим вариант, когда первый игрок выбрал 3, а второй 4, тогда выигрыш составит 5, но 5 – не является ценой игры. Если первый игрок выберет 3 стратегию, а второй, не зная об этом, выбрал 1, то получим 4 (эта ситуация выгодна второму игроку).

Рассмотренный метод решения игры называется метод минимакса. Этот метод приводит к решению только в случае существования седловой точки в матрице.

Понятие смешанной стратегии

Смешанная стратегия применяется при достаточно большом числе актов игры. В этом случае каждый из игроков может стремиться к тому, чтобы частота применения им каждой стратегии была равна определенному числу. В частности, игрок будет применять свою i-ю стратегию с частотой , а второй игрок своюj-ю стратегию с частотой , гдеN – число актов игры, k_i,l_j – число применяемых стратегий соответствующими игроками.

Тогда смешанной стратегией первого игрока будем называть набор , гдеp_i – вероятность применения первым игроком i^-ой чистой стратегии, т.е.

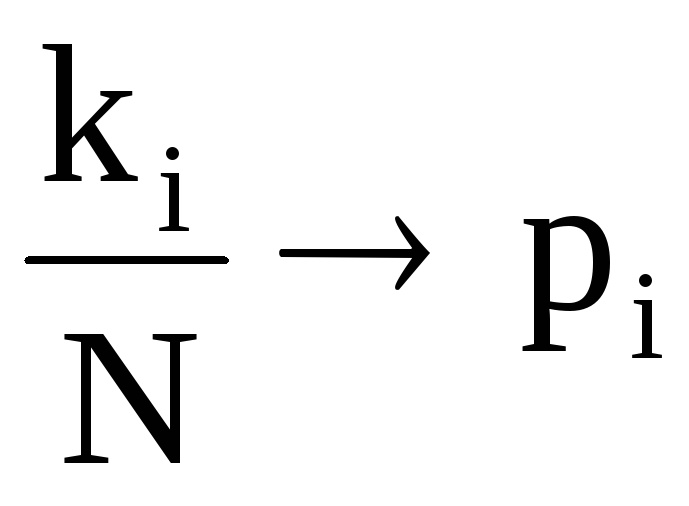при

Аналогично смешанная стратегия второго игрока: , где так же

при .

При этом, очевидно, что

Выигрыш при смешанных стратегиях

Естественно, что при применении смешанных стратегий нас интересует не выигрыш или проигрыш за одну партию, а средний выигрыш или проигрыш за много партий.

Если нам известна некоторая смешанная стратегия первого игрока, а второй игрок применяет j-ю чистую стратегию, т. е.

то под выигрышем первого игрока мы будем принимать следующее математическое ожидание:

Если же и второй игрок применит свою смешанную стратегию то средний выигрыш за большое число игр:

_.

Здесь h_ij – соответствующий элемент платежной матрицы.

Существование решения игры в смешанных стратегиях

Оказывается, что любая игра в смешанных стратегиях имеет решение, т.е. можно подобрать ипри которых гарантированный средний выигрыш первого игрока совпадает с гарантированным проигрышем второго игрока.

Теорема «О минимаксах»

Какова бы ни была игра (матрица H), оба игрока имеют оптимальные смешанные стратегии, при этом имеет место:

Значения и, при которых достигаются смешанные экстремумы образуют пару оптимальных стратегий.

Общее значение минимаксов называетсяценой игры, а решением игры называется цена игры и пара оптимальных стратегий.

Доказательство теоремы базируется на теории двойственности задач линейного программирования.