Бесконечные игры

Если хотя бы один из игроков имеет бесконечное число стратегий, то игра называется бесконечной. Для такой игры необходимо найти равновесную ситуацию.

Необходимое и достаточное условие существования игры

.

Имеет место следующая теорема:

Если является непрерывной функцией обоих аргументов на единичном квадрате, то оба игрока имеют оптимальные смешанные стратегии.

Известны только отдельные методы решения игр для отдельных специальных видов задач.

В частности, это имеет место для так называемых выпуклых игр.

Выпуклые игры

Функция φ(x) заданная на отрезке называется выпуклой, если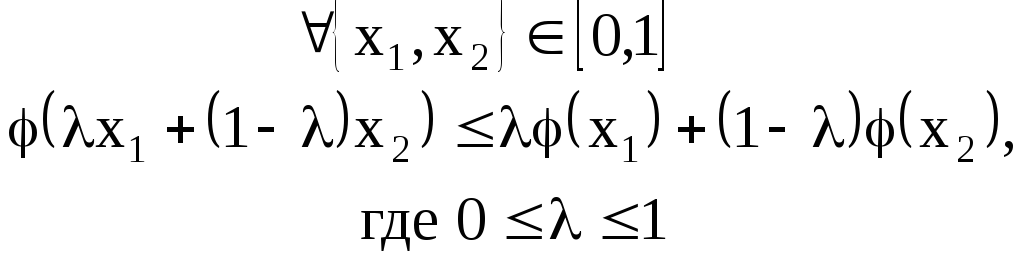

Функция называется строго выпуклой, если имеет место строгое неравенство.

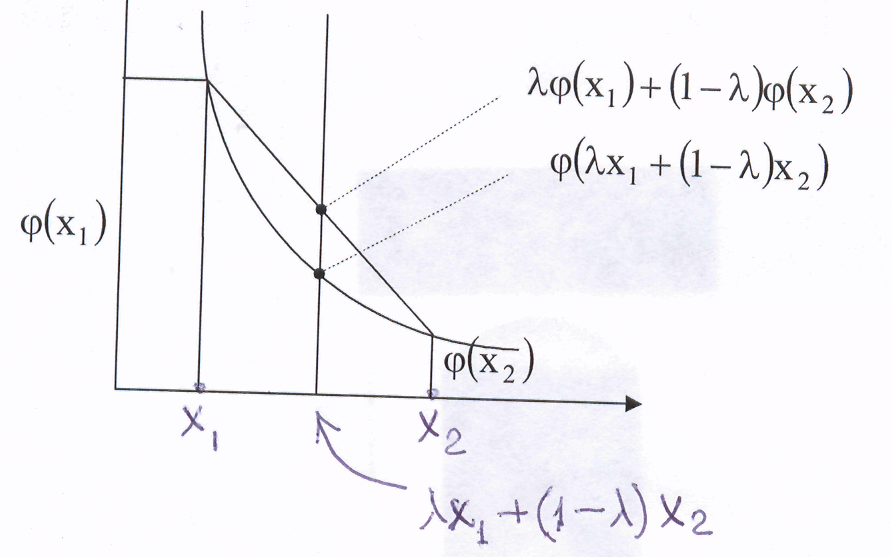
- выпуклая комбинация.

Выпуклость означает, что значение функции от выпуклой комбинации меньше либо равно выпуклой комбинации соответствующих значений функции.

Множество называется связным (односвязным), если любые две точки этого множества могут быть соединены кривой, целиком лежащей в этом множестве В противном случае множество называется многосвязным.

У выпуклой функции множество минимумов является связанным множеством. Если функция строго выпуклая, то минимум единственный. Это свойство используется для доказательства тех теорем, которые лежат в теории выпуклых игр.

Выпуклая игра.

Непрерывная антагонистическая игра, заданная на единичном квадрате (т.е. заданной при ,), называетсявыпуклой (строго выпуклой); если платежная функция H(x,y) выпукла (строго выпукла) по y при любом фиксированном x.

Теорема 1:

В выпуклой игре на единичном квадрате второй игрок имеет чистую оптимальную стратегию y*. Эта стратегия является решением уравнения

,

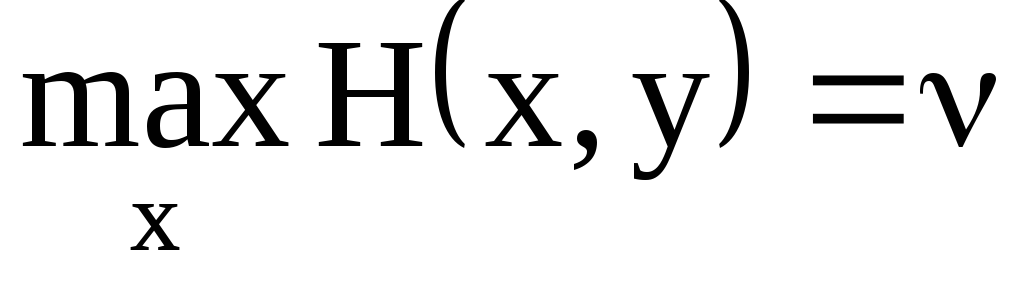относительно y, где ν – цена игры.

Особенность этого уравнения в том, что в нем две неизвестные величины – y и ν

Стратегия x первого игрока называется существенной если

.

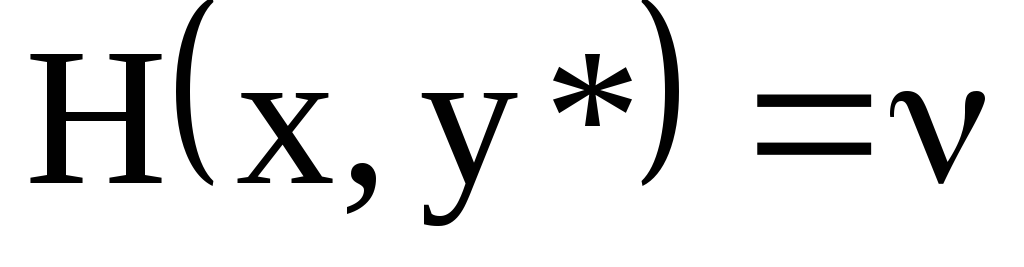Очевидно, что существенные стратегии первого игрока – это те x, на которых достигаются максимумы в уравнении теоремы.

Теорема 2:

Пусть Г – выпуклая игра, причем H(x,y) при любом x дифференцируема по y (на границах при y=0 и y=1 имеется в виду односторонняя производная). Пусть далее y* есть чистая оптимальная стратегия второго игрока, а ν – цена игры. Тогда:

1. если y*=1, то среди оптимальных стратегий первого игрока имеется такая существенная стратегия 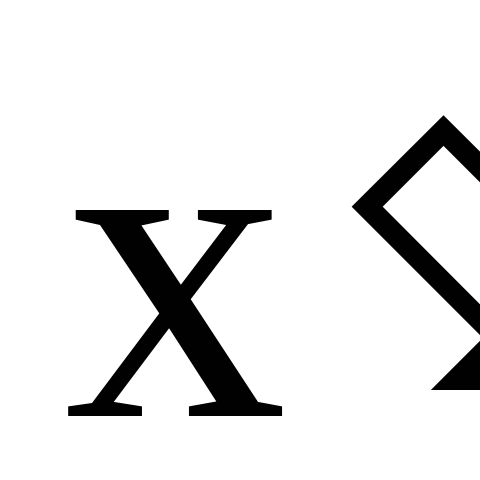, что;

2. если y*=0, то среди оптимальных стратегий первого игрока имеется такая существенная стратегия , что;

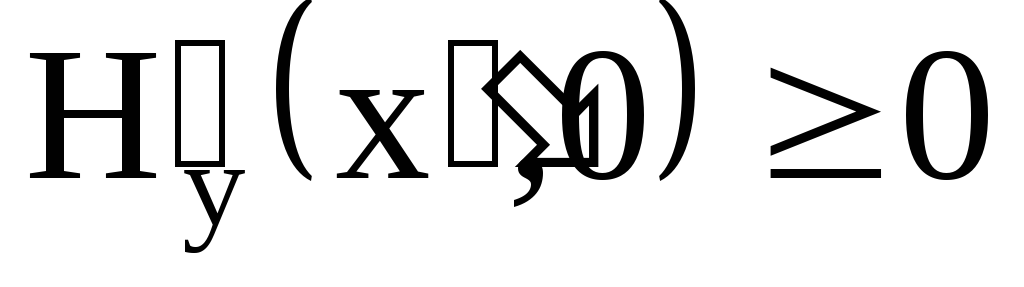3. если 0<y*<1, то среди оптимальных стратегий первого игрока имеются такие две существенные стратегии, что

;

При этом данная «смесь» стратегий _и образуют оптимальную смешанную стратегию первого игрока. Вероятности применения этих стратегий_и равны соответственноα и 1-α, где α удовлетворяет уравнению:

.

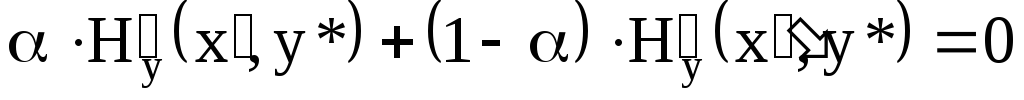Иллюстрация к условию теоремы 2

Пример: борьба за рынки.

Пусть фирма «1» пытается вытеснить фирму «2» с двух рынков сбыта, которые захвачены фирмой 2. Фирма 1 располагает для этого средствами, условно принятыми за единицу. Эти средства фирма 1 должна распространить между рынками:

x – на первый рынок,

1-x – на второй рынок

(x – есть параметр стратеги).

Фирма 2 так же располагает средствами равными единице, ее стратегия:

y – на первый рынок,

1-y – на второй рынок.

Пусть K₁ и K₂ – коэффициенты, характеризующие важность первого и второго рынков. Если фирма 1 имеет превышение вложений средств на первом рынке, т.е. x>y, то он получает выигрыш, пропорциональный этому превышению и ценности рынка, , т.е.

K₁(x-y).

Если наоборот x<y, тогда он получит превышение на втором рынке и выигрыш будет равен:

K₂(1-x-1+y)=K₂(y-x).

Таким образом, получаем следующую функцию:

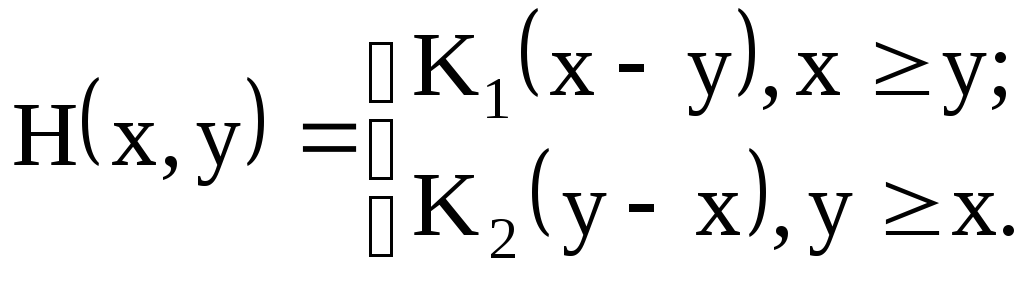
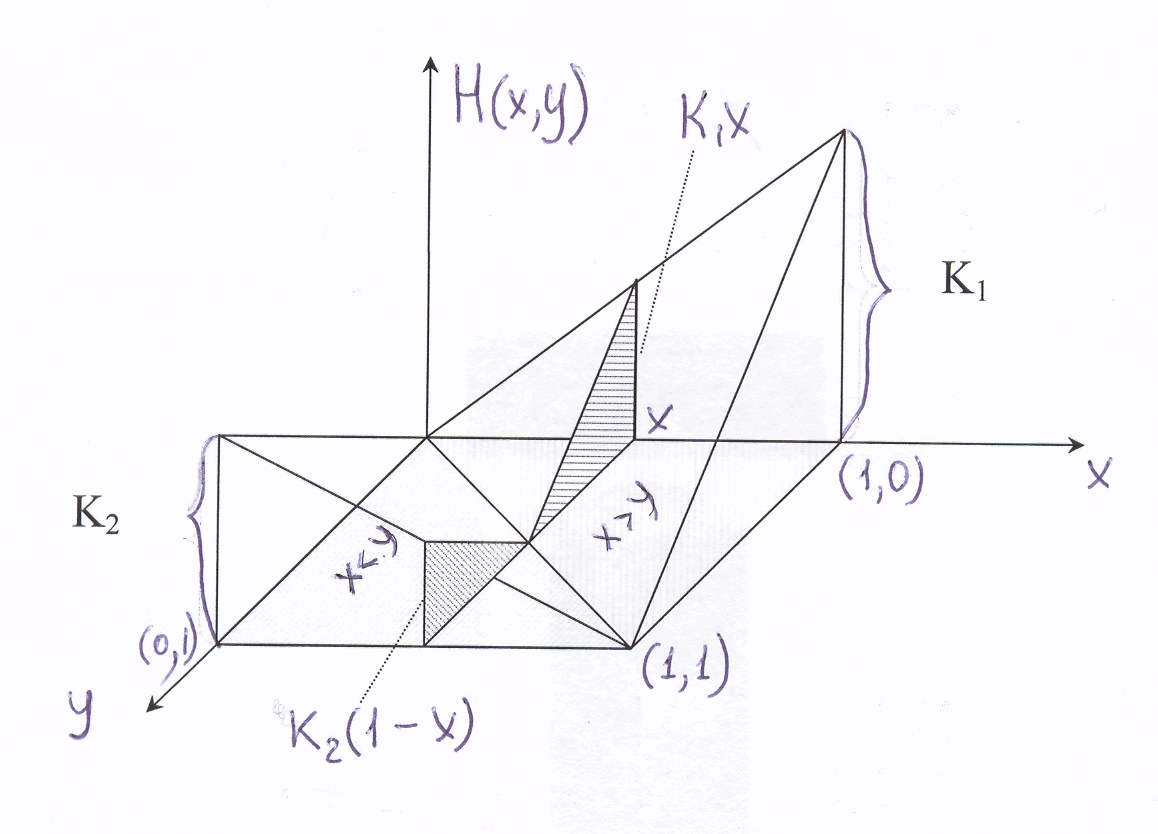
Платежная функция в игре «Борьба за рынки»

Найдем чистую оптимальную стратегию второго игрока y* и цену игры.

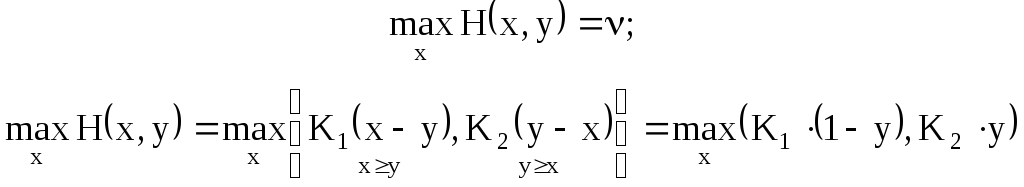
Второй игрок выбрал точку y* с той целью, чтобы при правильных рассуждениях фирмы_1 выигрыш был минимизированный.

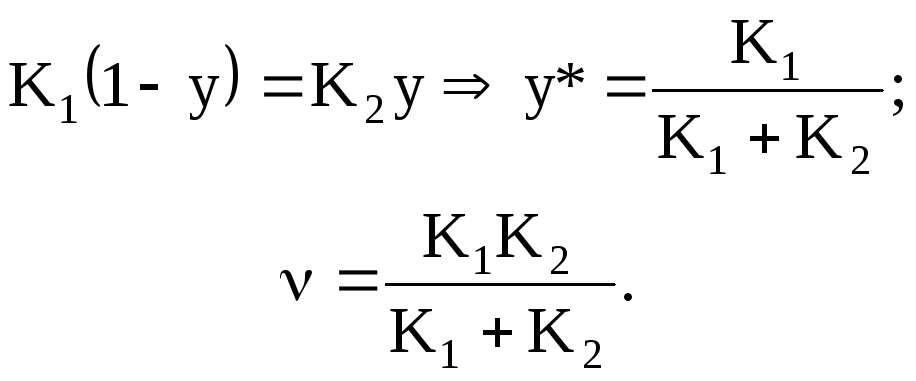
Для завершения игры необходимо найти и(существенные стратегии).

Если x>y*:

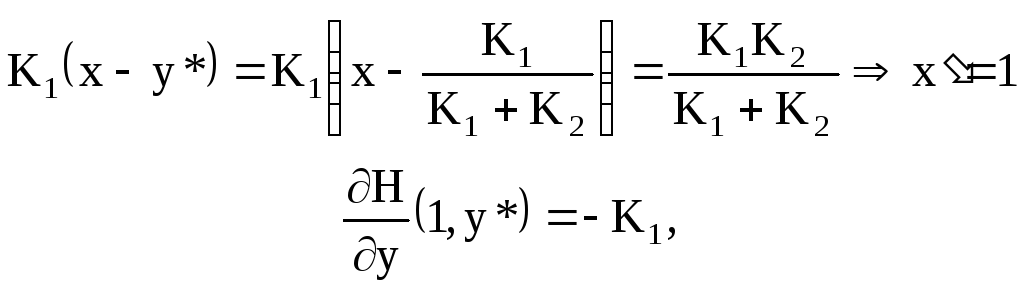
Если x<y*:

Вероятность α применения первым игроком своей стратегии:

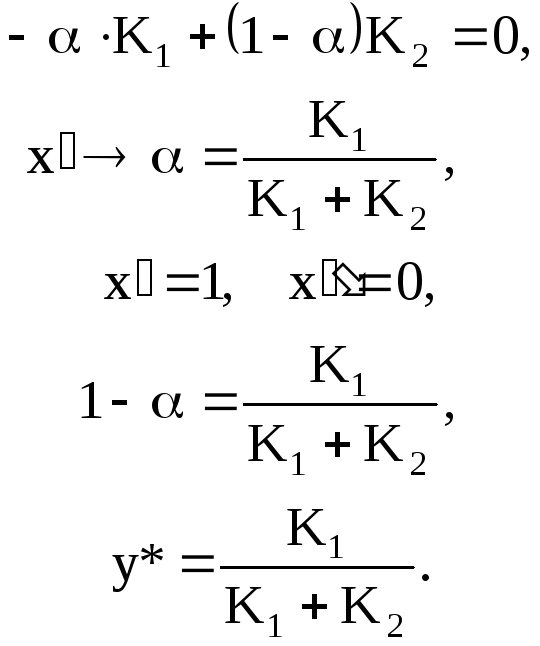
Первый игрок должен вкладывать средства с вероятностями обратно пропорциональными ценности рынка.

Решение игры.

Первый игрок вынужден вкладывать попеременно все свои средства на первом и втором рынке, причем с вероятностями обратно пропорциональными ценностям рынка.

Чем важнее рынок, тем больше в него средств вложил противник и тем труднее его оттуда вытеснить за счет превышения средств.