Целочисленные и комбинаторные задачи лп

В рассмотренных типичных задачах ЛП неизвестные компоненты плана могли принимать любые неотрицательные действительные значения. Этим не исчерпываются задачи ЛП и задачи математического программирования. Во многих важных задачах предполагается, что все или некоторые из компонент плана являются целочисленными. Частным случаем этого класса задач являются булевские задачи, в которых переменные принимают только два значения – 0 и 1. Другие задачи оптимизации имеют дело с комбинаторикой. Иногда эти задачи могут быть сведены к булевским задачам ЛП.

Мы переходим к знакомству с целочисленными задачами ЛП (ЦЗЛП)

Оказывается, что такие задачи гораздо сложнее непрерывных ЗЛП. Иногда выбирать из конечного множества (но достаточно большого), значительно труднее, чем из бесконечного, но непрерывного множества, так как мы лишаемся права использовать непрерывную математику.

Для большинства задач ЦЗЛП неизвестны эффективные методы их точного решения.. Перейдем к на

Задача о назначении

Задача о назначении является комбинаторной задачей оптимизации, но она легко приводится к булевской и, следовательно, к целочисленной задаче.

Пусть имеется n-вакансий и n-претендентов. Каждый претендент может занимать любую, но только одну вакансию. Будем считать, что число претендентов и вакансий совпадает.

Обозначения:

А={a_i }– множество претендентов;

B={b_j}– множество вакансий;

–матрица «штрафов» за то, что i-й претендент займет j-ю вакансию.

Задача о назначении (ЗН) формулируется так:

Необходимо найти такую биекцию (взаимнооднозначное отображение) f множеств А и В, чтобы общий штраф от реализуемого им назначения R был минимальным.

Ясно, что выбирать приходится из n! всевозможных вариантов биекций.

При малом n задачу можно решить методом перебора. Для доступных нам ЭВМ это целесообразно при .

Если претендентом a_i занята вакансия b_j, то мы будем писать f(i)=j.

С помощью этого обозначения минимизируемую величину общего штрафа R можно записать так

.

Итак, задача состоит в таком выборе биекции f, чтобы R была минимальной. По существу, речь идет о нахождении подходящей перестановке индексов. Поэтому задача является комбинаторной.

Сведем ее к целочисленной задаче ЛП или более точно к булевской задаче ЛП. Булевская задача – это не просто целочисленная задача. Здесь каждая компонента плана либо равна нулю, либо равна единице.

Для сведения задачи о назначении к булевской введем матрицу , размерностьюn *n. Элементы этой матрицы зададим так:

.

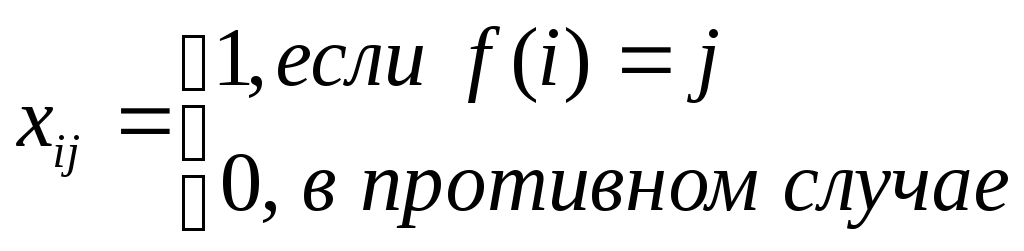Эта матрица обладает следующим свойствами.

В каждой строке и в каждом столбце матриц стоит по одной и только по одной единице, так как каждую вакансию должен занять один и только один претендент и каждый претендент должен занять одну и только одну вакансию. Это можно записать аналитически так:

С помощью элементов матрицы величинаR может быть записана

следующим образом:

Условие оптимизации, таким образом, имеет вид

Условие булевого характера задачи можно записать так:

. (5)

Таким образом, мы доказали, что ЗН является булевской, и, следовательно, целочисленной.

Данная задача очень похожа на транспортную задачу. Главное отличие заключается в условии (5). Кроме того, правые части системы ограничений (1), (2) имеют особенный вид – все они равны единице.

Пример применения задачи о назначении.

При сборке печатной платы роботом требуется найти минимальное распределение деталей по питателям так, чтобы суммарное расстояние от места хранения до места установки детали было минимальным.