
- •Глава 4. Дифференциальные уравнения движения смт и общие теоремы динамики смт
- •4.1. Дифференциальные уравнения движения смт
- •4.2. Теорема об изменении количества движения смт
- •4.3. Алгоритм решения задач с помощью теоремы об изменении количества движения смт – схема алгоритма д43 кдс с комментариями и примерами
- •Комментарии
- •Примечание
- •Пример 1
- •4.4. Теорема о движении центра масс смт
- •4.5. Алгоритм решения задач с помощью теоремы о движении центра масс смт – схема алгоритма д45 цмс с комментариями и примерами
- •Комментарии
- •Примечание
- •Пример 1
- •Найдем кинетический момент нмс, вращающейся относительно неподвижной оси Оz (рис. 33)
- •4.7. Алгоритм решения задач с помощью теоремы об изменении кинетического момента смт – схема алгоритма д47 кмс с комментариями и примерами
- •Комментарии
- •Примечание
- •Осевые моменты инерции однородных пластинок и стержней массы m
- •Пример 1
- •Пример 2
- •Пример 3
- •4.8. Теорема об изменении кинетической энергии смт
- •4.8.1. Три формы теоремы
- •4.8.2. Кинетическая энергия нмс в частных случаях движения
- •4.8.3. Теорема Кенига
- •4.8.4. Работа произвольной системы сил, приложенной к смт
- •4.9. Алгоритм решения задач с помощью теоремы об изменении кинетической энергии смт – схема алгоритма д49 кэс с комментариями и примерами
- •Комментарии
- •Пример 1
- •4.10.2. Потенциальная энергия мт
- •4.10.3. Примеры вычисления силовой функции и потенциальной энергии мт
- •Силовая функция линейной силы упругости определяется по формуле ,
- •4.10.4. Силовая функция и потенциальная энергия смт
- •4.10.5. Закон сохранения механической энергии мт
- •4.10.6. Закон сохранения механической энергии смт
4.8.2. Кинетическая энергия нмс в частных случаях движения
Поступательное движение НМС.
В
случае поступательного движения НМС
все ее точки движутся с одинаковыми
скоростями, равными скорости движения
центра масс НМС:
![]() .
Соотношение (4.30) в случае поступательного
движения НМС примет вид:
.
Соотношение (4.30) в случае поступательного
движения НМС примет вид:
![]() .
(4.38)
.
(4.38)
Вращательное движение НМС вокруг неподвижной оси z.
В
случае вращательного
движения
НМС все ее МТ движутся со скоростями
![]() ,
где
,
где![]() - кратчайшее расстояние от-й
МТ до оси вращения. Соотношение (4.30) в
случае вращательного
движения
НМС вокруг неподвижной оси z примет вид:
- кратчайшее расстояние от-й
МТ до оси вращения. Соотношение (4.30) в
случае вращательного
движения
НМС вокруг неподвижной оси z примет вид:
![]() .
(4.39)
.
(4.39)
Плоскопараллельное движение НМС.
В
случае плоскопараллельного
движения
НМС в каждый момент времени движение
НМС можно рассматривать как мгновенное
вращательное движение относительно
оси, перпендикулярной неподвижной
(основной) плоскости и проходящей через
мгновенный центр скоростей
![]() .
Поэтому можно использовать соотношение
(4.39)
.
Поэтому можно использовать соотношение
(4.39)
![]() ,
(4.40)
,
(4.40)
где
![]() – момент инерции НМС относительно
мгновенной оси, перпендикулярной к
неподвижной плоскости движения и
проходящей через мгновенный центр
скоростей.
– момент инерции НМС относительно
мгновенной оси, перпендикулярной к
неподвижной плоскости движения и
проходящей через мгновенный центр
скоростей.
Используем теорему Штейнера-Гюйгенса (3.22):
![]() ,
,
где JС – момент инерции НМС относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через центр масс С, а СРv – расстояние между мгновенным центром скоростей и центром масс.
Подставив это выражение в соотношение (4.40), получим:
![]() или
или
![]() , (4.41)
, (4.41)
где
![]() – скорость центра масс НМС.
– скорость центра масс НМС.
4.8.3. Теорема Кенига
Теорема: Кинетическая энергия СМТ в общем случае движения равна сумме кинетической энергии центра масс в предположении, что в нем сосредоточена вся масса СМТ, и кинетической энергии СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.
Доказательство.
Введем подвижную систему отсчета с началом в центре масс С, движущуюся поступательно относительно основной инерциальной системы отсчета. Представим скорость -й МТ, входящей в СМТ, относительно основной системы отсчета в виде (Ч.1 Кинематика):
![]() ,
где
,
где
![]() – скорость движения центра масс СМТ, а
– скорость движения центра масс СМТ, а![]() – скорость-й
точки СМТ по отношению к подвижной
системе отсчета.
– скорость-й
точки СМТ по отношению к подвижной
системе отсчета.
Подставив это выражение в соотношение (4.30), получим:

 (4.42)
(4.42)
где
![]() – масса всей системы,
– масса всей системы,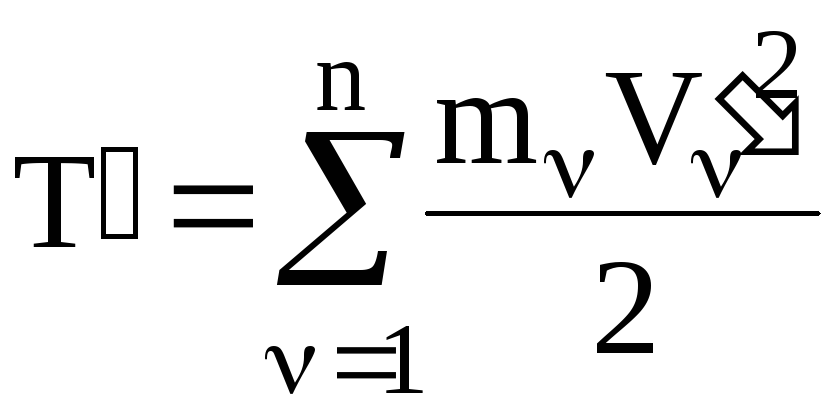 – кинетическая энергия СМТ при ее
движении относительно подвижной системы
отсчета, перемещающейся вместе с центром
масс поступательно.
– кинетическая энергия СМТ при ее
движении относительно подвижной системы
отсчета, перемещающейся вместе с центром
масс поступательно.
На основании соотношений (4.6) и (4.16) для суммы во втором слагаемом правой части выражения (4.42) можно записать:
![]() ,
так как
,
так как
![]() .
.
Из соотношения (4.42) имеем теорему Кенига:
![]() .
(4.43)
.
(4.43)
4.8.4. Работа произвольной системы сил, приложенной к смт
Пусть
к свободной СМТ приложена произвольная
система сил
![]() .
Выбрав в качестве полюса произвольную
точку О СМТ, на основании теоремы о
скорости точки СМТ в общем случае
движения (Ч.1 Кинематика) скорость
движения-й
МТ относительно неподвижной системы
координат выразится формулой:
.
Выбрав в качестве полюса произвольную
точку О СМТ, на основании теоремы о
скорости точки СМТ в общем случае
движения (Ч.1 Кинематика) скорость
движения-й
МТ относительно неподвижной системы
координат выразится формулой:
![]() ,
(4.44)
,
(4.44)
где
![]() – скорость полюса,
– скорость полюса,![]() – угловая скорость вращения СМТ вокруг
мгновенной оси, проходящей через полюс
О.
– угловая скорость вращения СМТ вокруг
мгновенной оси, проходящей через полюс
О.
Для
удобства сначала найдем мощность силы
![]() :
:
![]() .
.
Второе слагаемое по свойству смешанного произведения и с учетом формулы для момента силы относительно точки (Ч.2 Статика) может быть записано в виде:
![]() .
.
Подставляя это равенство в предыдущую формулу и используя определение скалярного произведения и связь между моментом силы относительно точки и оси (Ч.1 Статика), получим:
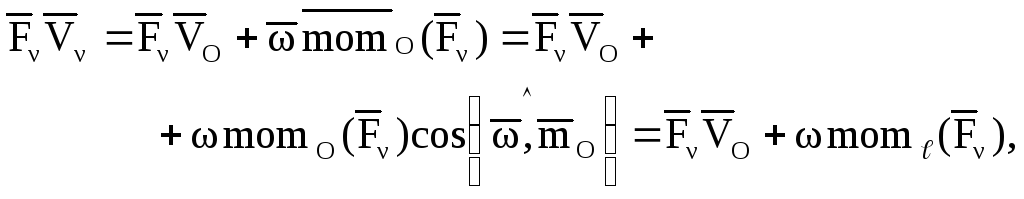
где
![]() – момент-й
силы относительно мгновенной оси
вращения ,
проходящей через полюс О.
– момент-й
силы относительно мгновенной оси
вращения ,
проходящей через полюс О.
Перейдем
к определению элементарной работы силы
![]() .
.
Учтя
соотношения
![]() ,
,![]() ,
,![]() ,
получим:
,
получим:
![]() +
+![]() .
.
Тогда элементарная работа всех сил, действующих на СМТ, равна:
 +
+
![]() +
+![]() ,
,
где
![]() - сумма работ всех сил, действующих на
СМТ,
- сумма работ всех сил, действующих на
СМТ,
![]() - главный вектор, а
- главный вектор, а![]() - проекция главного момента на ось
системы сил, действующих на СМТ.
- проекция главного момента на ось
системы сил, действующих на СМТ.
Работа системы сил, действующих на СМТ, примет вид:
А= .
(4.45)
.
(4.45)
В случае поступательного движения НМС соотношение (4.45) примет вид:
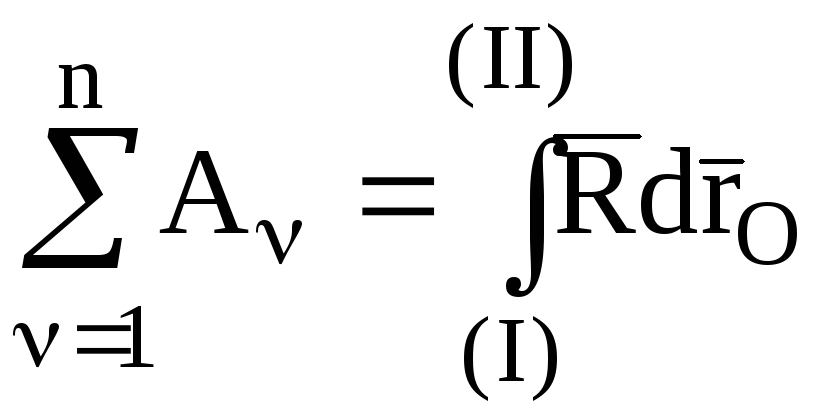 .
.
В случае вращательного движения НМС относительно неподвижной оси z соотношение (4.45) примет вид:
 .
.
В
случае, когда момент постоянен (![]() ),
его работа выразится формулой:
),
его работа выразится формулой:
![]() .
.
