Глава 3. Основные понятия динамики СМТ

3.1. Внешние и внутренние силы,

свойства внутренних сил

Пусть СМТ состоит из n МТ (В₁, В₂, …, В_n), массы которых соответственно m₁, m₂,…,m_n.

В динамике СМТ вводится следующая классификация сил:

Внешними силами для данной СМТ называются силы, с которыми действуют на нее объекты, не входящие в рассматриваемую СМТ.

Внутренними силами для данной СМТ называются силы взаимодействия между МТ, входящими в рассматриваемую СМТ.

Обозначим через и соответственно равнодействующие внешних и внутренних сил, действующих на -ю МТ.

По закону равенства действия и противодействия внутренние силы, действующие на две произвольно выбранные МТ, входящие в СМТ, равны по модулю и направлены по одной прямой в противоположные стороны (рис. 22):

. (3.1)

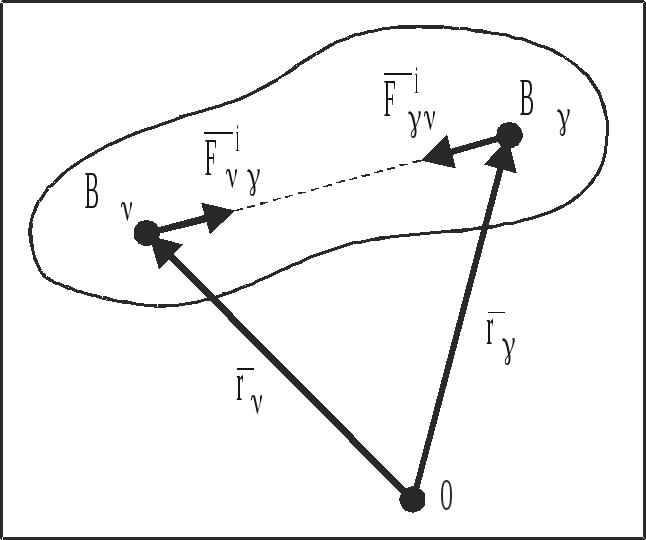
Рис. 22

Используя этот закон, получим два следующих свойства внутренних сил СМТ:

• главный вектор всех внутренних сил, действующих на СМТ, всегда равен нулю:

; (3.2)

• главный момент всех внутренних сил, действующих на СМТ, относительно произвольного центра всегда равен нулю:

. (3.3)

В справедливости соотношения (3.3) можно убедиться, подсчитав сумму моментов внутренних сил, приложенных к двум произвольно выбранным МТ, входящим в СМТ, относительно любого центра.

Используя формулу момента силы относительно точки (Ч.2 Статика) и свойство внутренних сил (3.1), получим:

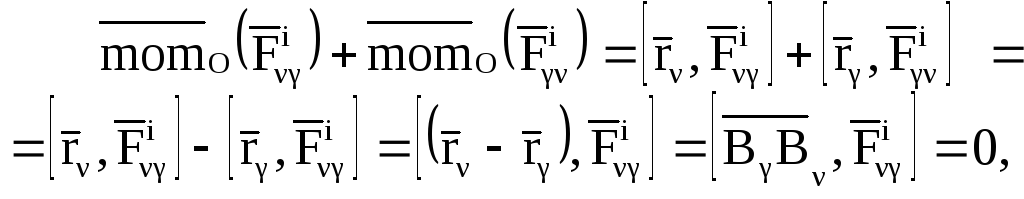
так как .

Все внутренние силы попарно равны по модулю и противо-положны по направлению, поэтому сумма моментов всех внутренних сил относительно произвольного центра также будет равна нулю.

3.2. Центр масс СМТ

Определение: Центром масс СМТ называется геометричес-кая точка C, радиус-вектор которой определяется выражением:

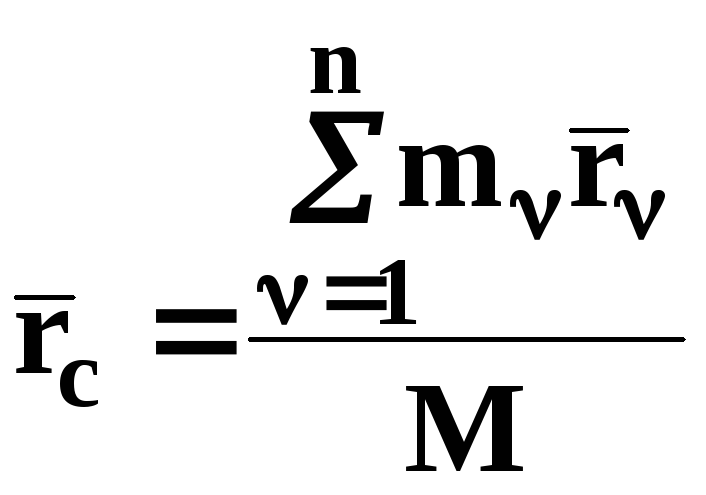, (3.4)

где М – масса СМТ, которая определяется соотношением:

. (3.5)

Спроектировав соотношение (3.4) на оси декартовой системы координат, получим формулы для координат центра масс СМТ:

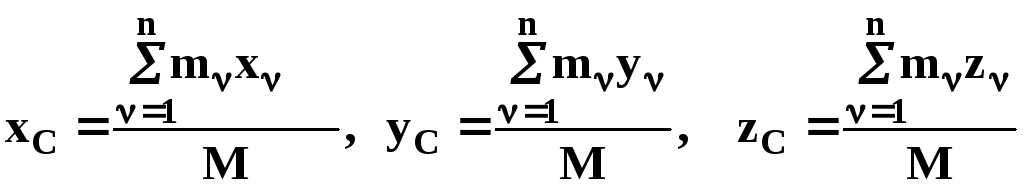. (3.6)

Можно доказать, что положение центра масс СМТ не зависит от выбора системы координат, в которой оно определяется. Для этого достаточно определить положение центра масс СМТ относительно двух произвольно выбранных систем координат и использовать формулы перехода от одной системы координат к другой.

3.3. Моменты инерции СМТ

3.3.1. Определения моментов инерции относительно точки, оси и плоскости

Пусть СМТ состоит из n МТ с массами ,,…,.

Определения:

Моментом инерции СМТ относительно точки О – J_O называется сумма произведений масс МТ на квадраты их расстояний – до точки О:

. (3.7)

Моментом инерции СМТ относительно оси (например, оси ) – называется сумма произведений масс МТ на квадраты их расстояний – h_ до оси :

. (3.8)

Моментом инерции СМТ относительно плоскости П – J_П называется сумма произведений масс МТ на квадраты их расстояний – d_ до плоскости П:

. (3.9)

Для того чтобы найти моменты инерции для НМС, необходимо НМС разбить на n элементарных частей, записать формулы (3.7) – (3.9) и в них перейти к пределу при n:

, (3.10) , (3.11)

, (3.12)

где dm – масса элементарной частицы НМС.

3.3.2. Моменты инерции относительно начала координат,

координатных осей и координатных плоскостей декартовой системы координат

Моменты инерции СМТ относительно начала координат, координатных осей и координатных плоскостей декартовой системы координат (рис. 23) на основании соотношений (3.7)–(3.9) можно записать в виде:

. (3.13)

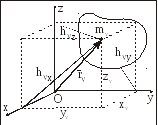
Рис. 23

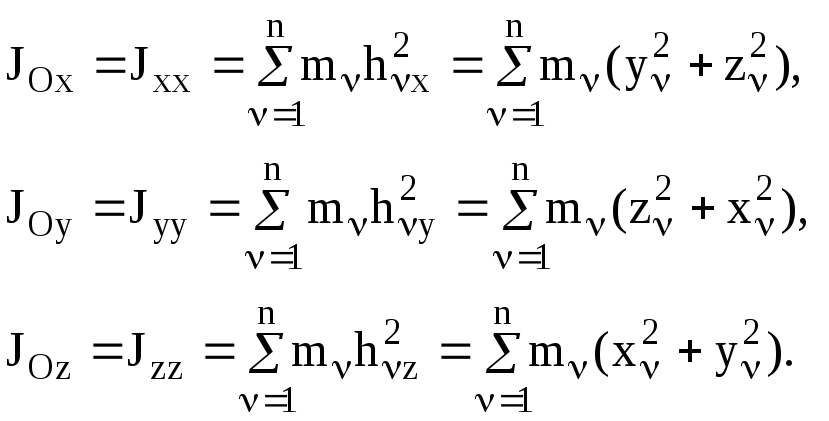(3.14)

(3.15)

Из полученных формул следуют свойства вышеназванных моментов инерции:

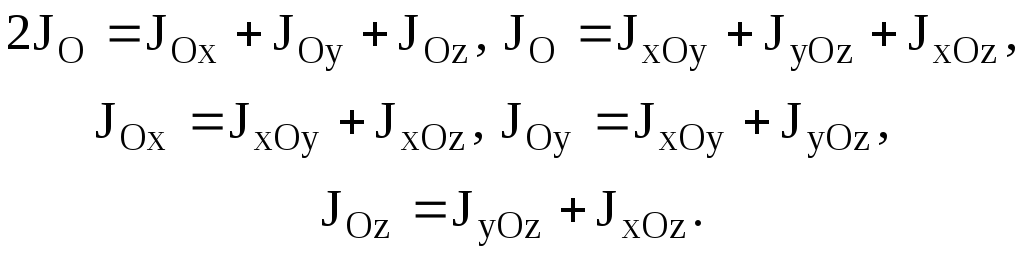(3.16)

3.3.3. Частные случаи моментов инерции

 Момент инерции однородного тонкого стержня массы М длиной  относительно оси, проходящей через конец стержня перпендикулярно к нему (рис.24).

Используя соотношение (3.11) и учтя, что , получим:

. . (3.17)

Рис. 24

Если ось z' проходит через середину стержня, то, изменив пределы интегрирования, несложно получить:

. (3.18)

 Момент инерции однородной окружности (тонкого кольца) массы М радиуса  относительно оси, проходящей через центр окружности перпендикулярно ее плоскости (рис. 25).

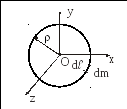
Рис. 25

Используя соотношение (3.11) и учтя, что

,

получим:

.

. (3.19)

Момент инерции однородного кругового полого цилиндра относительно его оси определяется также по соотношению (3.19).

 Момент инерции однородного тонкого диска массы М радиуса  относительно оси, проходящей через его центр перпендикулярно его плоскости (рис. 26).

Рис. 26

Используя соотношение (3.11) и учтя, что

( – площадь бесконечно тонкого кольца), получим:

. . (3.20)

Момент инерции однородного круглого сплошного цилиндра относительно его оси определяется также соотношением (3.20).

 Радиус инерции. В случае сложной конфигурации НМС его момент инерции определяется экспериментально и может быть выражен через радиус инерции. В этом случае момент инерции определяется по формуле:

, (3.21)

где ­­­­­– радиус инерции.

3.3.4. Теорема о моментах инерции относительно параллельных осей – теорема Штейнера-Гюйгенса

Теорема: Момент инерции СМТ относительно любой оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс, и произведения массы СМТ на квадрат расстояния между осями.

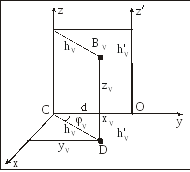
Рис. 27

Пусть известен момент инерции СМТ относительно оси Cz, проходящей через ее центр масс С. Найдем момент инерции СМТ относительно оси Оz', параллельной оси z и отстоящей от нее на расстояние d (рис. 27).

Начало декартовой системы координат выберем в центре масс С, ось Сy проведем так, чтобы она пересекала ось Оz'.

Возьмем произвольную точку В_ СМТ массы m_ с координатами x_, y_, z_. Расстояние от этой точки до оси Cz – h_, а до оси Оz' – .

На основании соотношения (3.8) момент инерции СМТ относительно оси Оz' имеет вид:

.

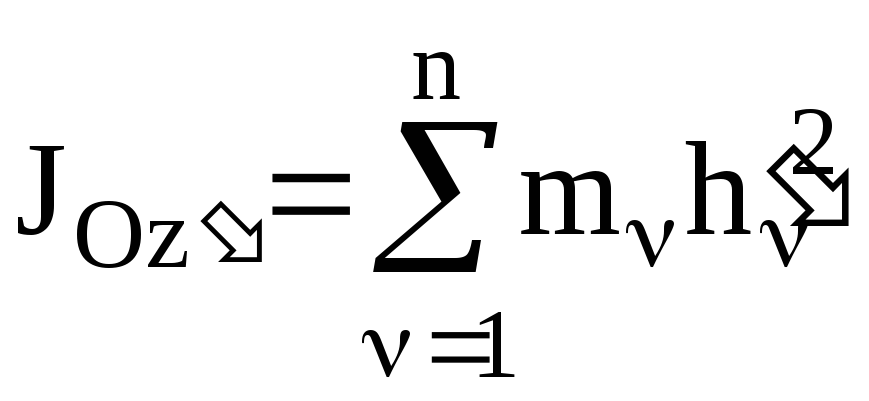Для треугольника СОD из теоремы косинусов следует, что

,

или

, так как .

Подставив в выражение для , будем иметь:

.

Так как , и ,

то для получим:

, (3.22)

что и требовалось доказать.

3.3.5. Моменты инерции относительно пучка прямых,

эллипсоид инерции, главные оси

Выбираем систему декартовых координат с началом в центре О. Проведем через начало координат произвольную ось О, образующую с осями координат Ох, Оу и Оz соответственно углы (рис. 28).

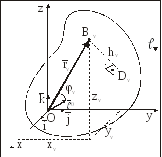
Рис. 28

На основании соотношения (3.8) для момента инерции СМТ относительно оси O имеем:

. (3.23)

Для прямоугольного треугольника OD_B_ можно записать

, (3.24)

где ,

(3.25)

Здесь – единичный вектор оси О.

Преобразуем соотношение (3.24), с учетом формулы (3.25) и соотношения , следующим образом:

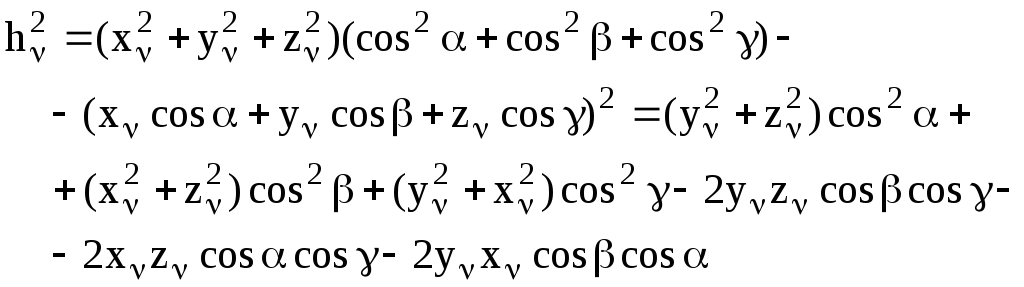(3.26)

Подставим соотношение (3.26) в соотношение (3.23):

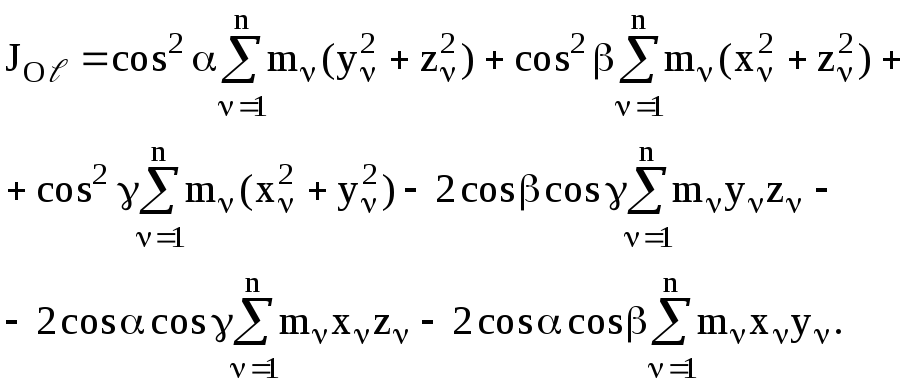(3.27)

Учтем, что на основании соотношений (3.14) можно записать:

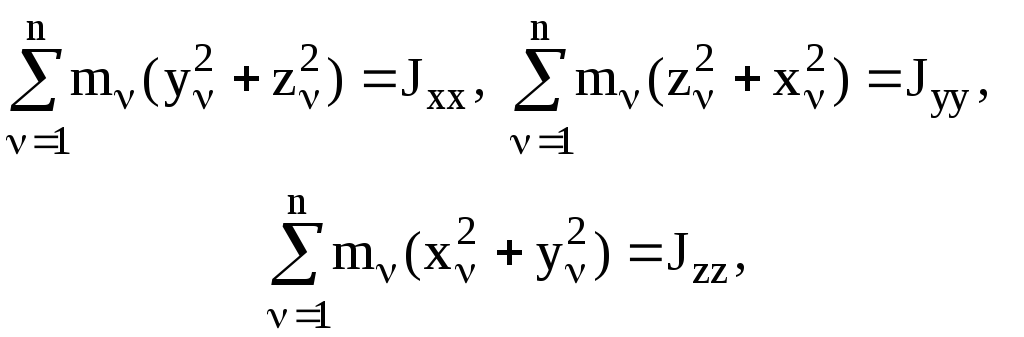(3.28)

где J_xx, J_yy, J_zz – моменты инерции СМТ относительно координатных осей. Величины

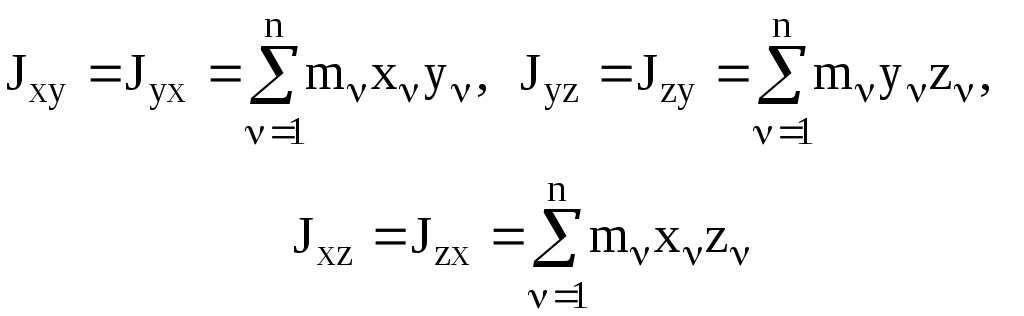(3.29)

называются произведениями инерции или центробежными моментами инерции СМТ.

С учетом (3.28) и (3.29) соотношение (3.27) примет вид:

(3.30)

Из равенства (3.30) следует, что для определения момента инерции СМТ относительно любой оси, проходящей через начало координат О, достаточно знать шесть величин J_xx, J_yy, J_zz, J_xy, J_yz, J_xz и направление этой оси, определяемое косинусами углов , , . Шесть величин J_xx, J_yy, J_zz, J_xy, J_yz, J_xz зависят от положения точки О и от направления координатных осей, так как с их изменением изменяются x_, y_, z_. Указанные величины можно расположить в виде симметричной матрицы:

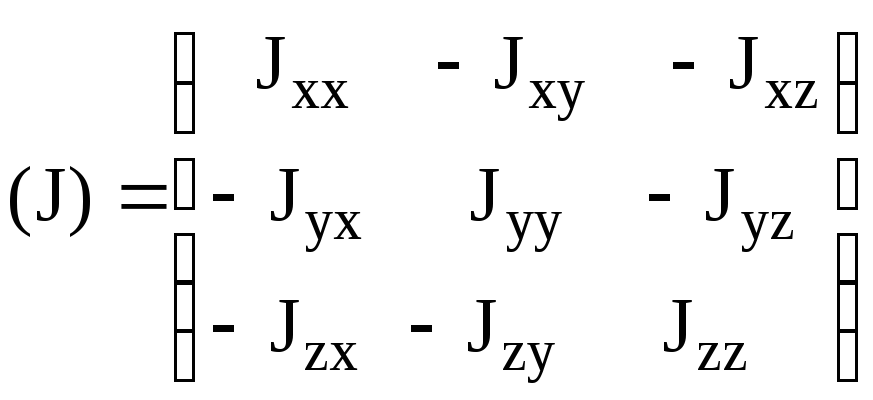, (3.31)

которая называется тензором инерции, элементы этой матрицы называются компонентами тензора инерции.

Для характеристики распределения моментов инерции СМТ относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка – эллипсоид инерции. Для построения этой поверхности на каждой оси , проходящей через точку , откладывается вектор , модуль которого равен:

. (3.32)

Выразим косинусы углов через координаты вектора :

(3.33)

Подставив в соотношение (3.30) формулы (3.33), получим уравнение поверхности второго порядка:

. (3.34)

Геометрическое место концов вектора располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.

Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции – главными центральными моментами инерции.

Если уравнение эллипсоида инерции отнести к его главным осям Ox', Oy', Oz', то оно примет вид:

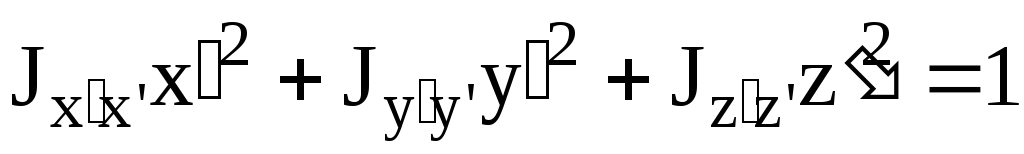, (3.35)

где x', y', z' – текущие координаты точки, расположенной на эллипсоиде инерции, относительно главных осей инерции; – главные моменты инерции.

Центробежные моменты инерции относительно главных осей инерции равны нулю

.

53