3.3. Метод итерации для нелинейной системы уравнений

Пусть требуется найти действительные решения системы двух уравнений с заданной точностью

.

Для этого перепишем исходную систему в приведенном (итерационном) виде: . Пустьи – начальные приближения корней, полученные графическим или каким-либо дру­гим способом. Подставив эти значения в правые части приведенной системы уравнений, мож­но получить

Аналогично можно получить второе приближение

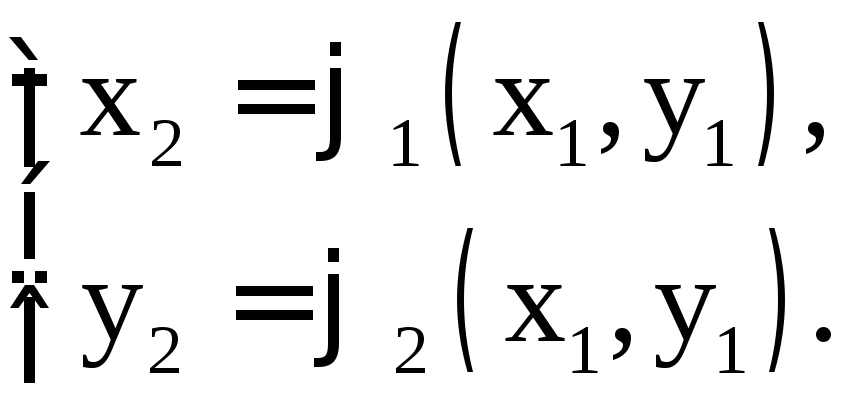
В общем случае Если функциии

непрерывны и последовательности исходятся, то пределы их дают решение приведенной, следовательно, и исходной системы.

Сходимость метода

Теорема. Пусть в некоторой замкнутой окрестности имеется одно и толь­ко одно решениеиприведенной системы.

Тогда если:

1) функции иопределены и непрерывно дифференцируемы в;

2) начальные приближения , и все последующие приближения ,при­над­лежат;

3) в выполнены неравенства или

неравенства ,то процесс последовательных приближений сходится к решению ,.

Оценка погрешности -го приближения определяется неравенством:

,

где – наибольшее из чисели, входящих в эти неравенства.

Сходимость метода считается хорошей, если ; при этом. Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.

Пример. Методом итерации решить систему с точностью до .

Решение.

1) Приведем систему к форме:

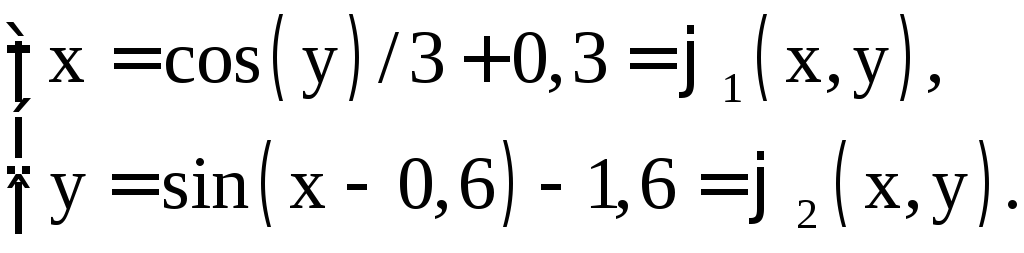
2) Для нахождения начального приближения отделим корни. Построив два графика ии най­дя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в об­ластии.

3) Проверим приведенную систему на сходимость итерационного процесса:

Следовательно,

и т.е. условия сходимости выполняются.

4) Для поиска последовательных приближений используют формулы:

Выберем следующие начальные значения: .

	0,15	0,1616	0,1508	0,1539	0,1510	0,1519	0,1510
	-2	-2,035	-2,0245	-0,0342	-2,0313	-2,0341	-2,0333

Поскольку , тои.

3.4. Метод скорейшего спуска решения нелинейных систем

Сущность метода скорейшего спуска заключается в том, что искомое решение системы рассматривается как минимум некоторой функциив-мерном пространстве, и этот минимум ищется в направлении, противоположном направлению градиента функции, то есть в направлении скорейшего убывания этой функции. Фунциясвязана с функциямиисходной системы соотношениями:

.

Пусть точка является начальным приближением к искомому решению. Через эту точку проводится поверхность уровня, а также нормаль к данной поверхности, которая указывает направление скорейшего убывания функции. Точка, в которой нормаль касается новой поверхности уровня, будет следующим приближением к исходному решению. Нормаль, проведенная к этой поверхности через точку, даёт возможность дойти до точки, в которой нормаль касается какой-то другой поверхности, и т. д.

Так как , гдето последовательность точек,,… приведет к минимальному значению функции, т. е. к искомому решению исходной системы.

Последовательные приближения определяются из матричного равенства , где черезобозначен вектор в-мерном пространстве, указывающий координаты точки, т. е. значение-го приближения;– параметр, характеризующий изменение функциивдоль соответствующей нормали,– градиент функциив точке.

В общем случае параметр может быть найден из уравнения:

, (1)

где – скалярная функция, определяющая изменение функции. При этом берется наименьший положительный корень уравнения (1).

Если считают малой величиной и не учитывают членов, содержащихво второй и высших степенях, то приближенно искомое решение можно найти из матричных равенств,,, где

,

,

.

Важным достоинством метода скорейшего спуска является его неизбежная сходимость. Поэтому его рекомендуется применять для уточнения решения в тех случаях, когда другие итерационные методы расходятся.

Пример. Методом скорейшего спуска приближенно вычислить корни системы:

Решение. Пусть .

Здесь и.

Подставляя нулевое приближение, будем иметь

, ,,,,

.

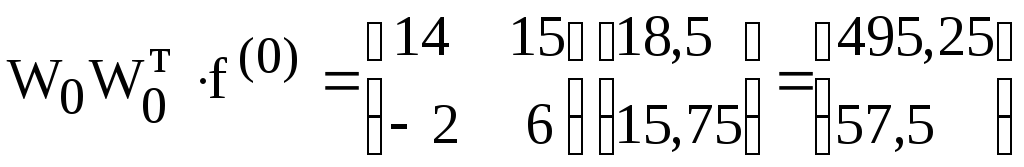Вычислим .

Аналогично найдем второе приближение

.

Тогда .

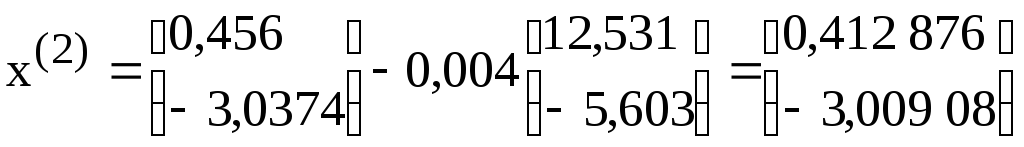Для контроля вычислим невязку: и так далее.

Получаем решение системы: