12.4.3. Изображение производных высшего порядка.

Изображение второй производной:

(12.8)

Пусть не только рассматриваемая функция , но и все ее производные до -го порядка включительно равны нулю при Тогда для изображения производной -го порядка имеем:

(12.9)

Пусть нам известны изображения нескольких функций:

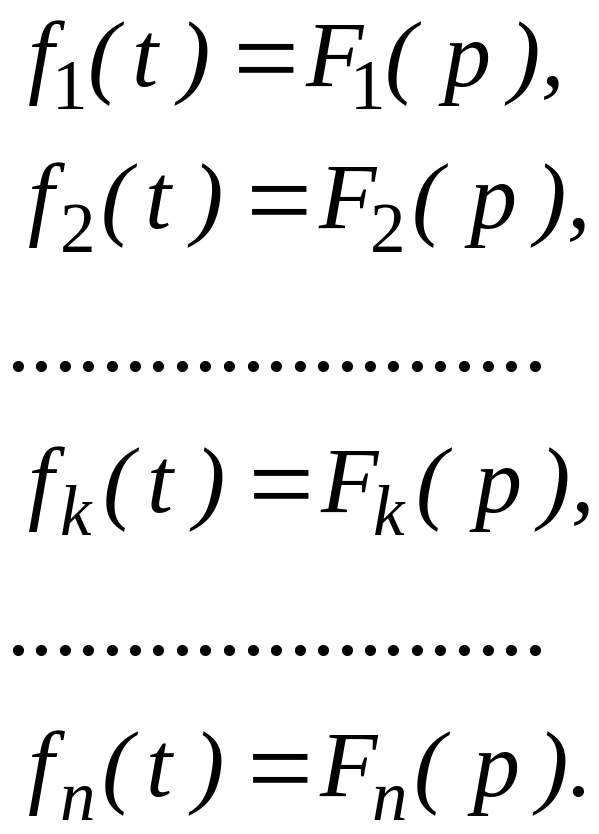
Тогда из основных свойств определенных интегралов имеем:

(12.10)

т.е. изображение суммы функций равно сумме изображений слагаемых.

Кроме того, из основных свойств определенных интегралов при имеем:

(12.11)

т.е. при умножении функции на постоянный коэффициент ее изображение должно быть умножено на этот коэффициент.

12.5. Изображение простейших функций по Лапласу

Таблица 1

№	Оригинал	Изображение
1
2
3
4
5
6
7	1-
8
9
10
11
12
13
14

12.6. Закон Ома в операторной форме

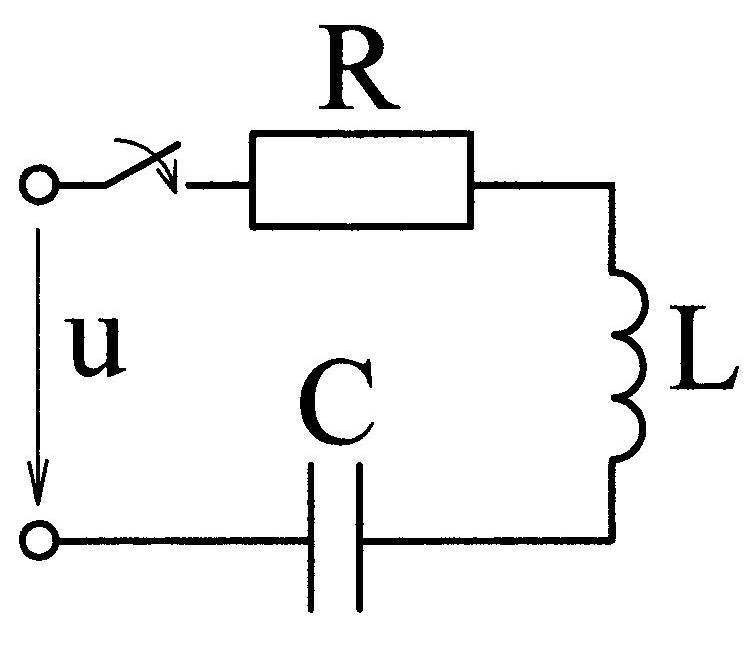
Рассмотрим цепь с последовательным соединением Пусть эта цепь включается под действие напряжения

Тогда имеем:

Рис. 12.1 (12.12)

Заменим в уравнении (12.12) на

: (12.13)

(12.14)

Так как то уравнение (12.14) в классической форме запишем в операторной форме с учетом (12.5) и (12.7):

откуда 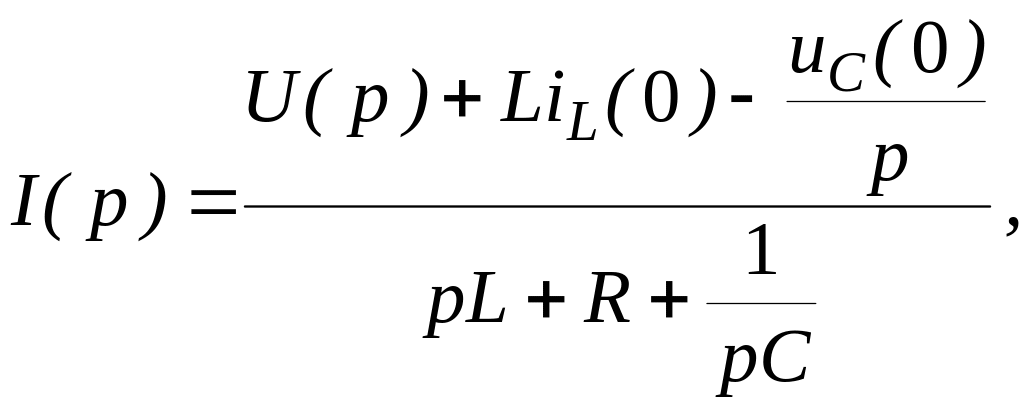(12.15)

или 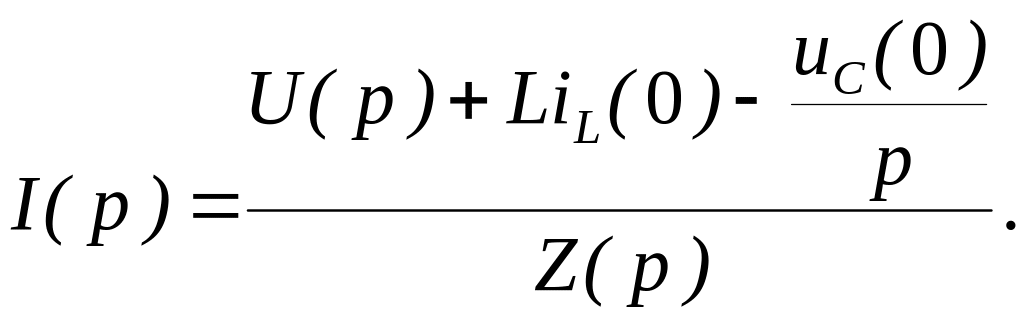(12.16)

Полученное выражение называется законом Ома в операторной форме при ненулевых начальных условиях; называется операторным сопротивлением цепи с последовательным соединением Структура его аналогична структуре комплекса сопротивления той же цепи переменному току, если заменить на р:

;

Слагаемое в выражении (12.15) представляет собой внутреннюю ЭДС, обусловленную запасом энергии в магнитном поле индуктивности L вследствие протекания через нее тока непосредственно до коммутации.

Слагаемое представляет собой внутреннюю ЭДС, обусловленную запасом энергии в электрическом поле конденсатора вследствие наличия на нем напряжения непосредственно до коммутации.

Для нулевых начальных условиях, т.е. при выражение (12.16) примет вид:

(12.17)

Выражение (12.17) называется законом Ома в операторной форме при нулевых начальных условиях.