§8 Методы разложения функций в ряд Тейлора

Разложение функций в ряд Тейлора, по определению, часто связано с громоздкими вычислениями при нахождении производных и сложностью исследования его сходимости. Приведем несколько методов, когда этого можно избежать

Использование формулы суммы бесконечной убывающей геометрической прогрессии

Разложить в ряд Тейлора в окрестности точки функциюРешение т.к.

то при

Метод подстановки

Разложить функцию по степеням.

Решение : Запишем следующую цепочку равенств

Возвращаясь к старой переменной х по формуле , получаем

.

Метод интегрирования

Разложить в ряд Маклорена функцию

Решение т.к. , то

;

Метод дифференцирования

Разложить в ряд Маклорена функцию

Решение. Так как , то

Для разложения используются и другие методы.

§ 9. Приложения рядов

Приближенное вычисление значений функций.

Для нахождения приближенного значения функции f(x) в точке

с заданной точностью поступим следующим образом. Разложим функцию f(x) в ряд по степеням с интервалом сходимости, содержащим точку, где- точка , в которой значение функции и ее производных вычисляются легко и точно. Переменной х придадим значениеи в полученном числовом рядуоставим только члены, гарантирующие только заданную точность вычислений. Минимаьное числотаких членов определим из соответствующей оценки либо остатка формулы Тейлора , либо остатка ряда.

Пример. Вычислить с точностью число е.

Решение. Так как

то из оценки

следует, что , т.е. необходимо взять пять слагаемых .

Пример 2. Вычислить с точностью 0,0001.

Решение Так как и ряд

является рядом Лейбница, то из оценки

получаем . Таким образом

Приближенное вычисление интегралов

Пример Вычислить c точностью 0,001

Решение. Имеем :

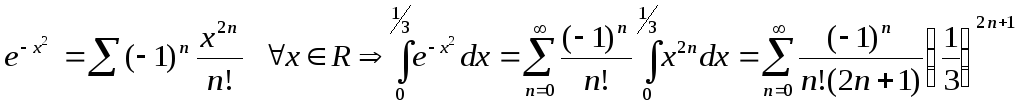
Оценим погрешность

тогда

Интегрирование дифференциальных уравнений

Степенные ряды могут применяться для нахождения приближенного решения дифференциального уравнения, если его решение не удается найти в элементарных функциях.

Пример. Найти решение дифференциального уравнения

удовлетворяющее начальному условию

Решение. Уравнение допускает разделение переменных :

однако интеграл от левой части уравнения не выражается в элементарных функциях. Будем искать решение в виде ряда Маклорена

Так как , а(*) то.

Дифференцируя по х обе части равенства (*), находим

; (**)

откуда

;

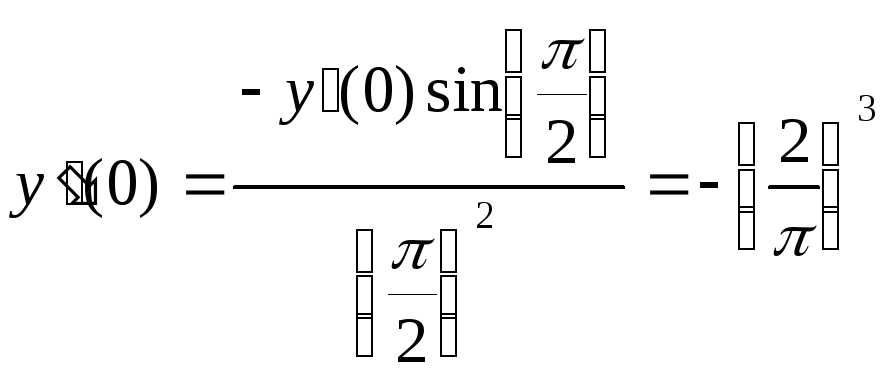Дифференцируя обе части равенства (**) , находим . Продолжая этот процесс, можно получить любое число членов разложения в ряд Маклорена искомого решения

Глава 16 Ряды Фурье

§1.Ортонормированные системы.

Определение: Евклидовым пространством называют линейное пространство L, в котором задано скалярное умножение, т.е. отображение f:LR, ставящее упорядоченной паре элементов пространства L в соответствие число и удовлетворяющее аксиомам скалярного умножения :

1.(x,y)=(y,x), x,y_L;

2.(x+y,z)=(x,z)+(y,z), x,y,zL;

3.(x,y)=(x,y), x,yL, R;

4.(x,x)_ 0, и (x,x)=0  x=0.

Определение: Линейное (евклидово) пространство бесконечномерное, если в нем можно выбрать любое количество линейно независимых элементов.

Определение: Функция называется кусочно -непрерывной на отрезке [a;b], если она непрерывна всюду на отрезке [a;b] за исключением конечного числа точек, в которых эта функция имеет разрывы первого рода.

Так функция

f(x)=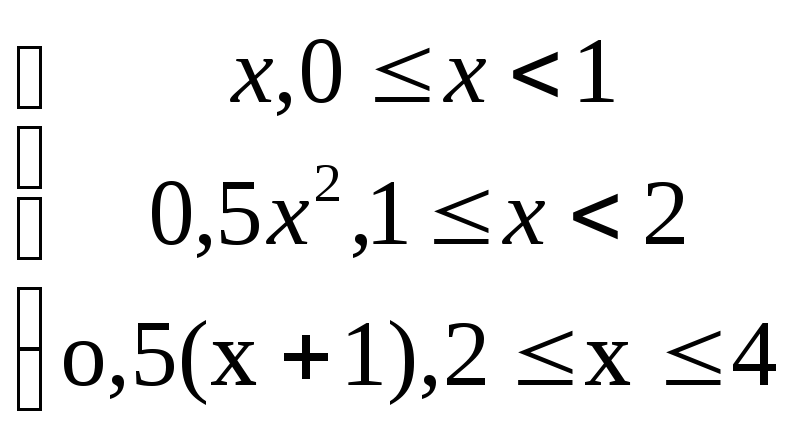

является кусочно-непрерывной на отрезке [0;4].

Множество всех кусочно-непрерывных на [a;b] функций образует линейное пространство. При этом под сложением элементов линейного пространства и умножением элемента на число понимают обычные операции сложения функций и умножения функции на число. Нулевым элементом в этом линейном пространстве является функция, тождественно равная нулю.

Произведение любых двух функций f и g из рассматриваемого линейного пространства является кусочно-непрерывной функцией, и, следовательно, интегрируемой на отрезке [a;b] функцией. Значит в этом линейном пространстве определено отображение, которое любым двум функциям f и g ставит в соответствие действительное число (f,g):

(f, g)= (1)

Формула (1) задает скалярное умножение в рассматриваемом линейном векторном пространстве кусочно-непрерывных функций.

Легко проверить, что данное отображение удовлетворяет первым трем аксиомам скалярного умножения. Аксиома (4) не выполняется, действительно:

(f, f)==0

Для любой функции f(x), равной нулю на [a;b] всюду, кроме некоторого конечного числа точек. Такая функция кусочно-непрерывна на [a; b], но не является нулевым элементом линейного пространства, т.к. она не равна тождественно нулю на всем отрезке [a; b] .

Чтобы четвертая аксиома скалярного умножения для введенного отображения выполнялась, будем рассматривать только те кусочно-непрерывные на отрезке [a;b] функции f(x), значения которых в каждой внутренней точке их разрываравны полусумме правого и левого пределов в этой точке:

(2)

Значения на границах отрезка [a;b] одинаковы и равны полусумме односторонних пределов функции в этих точках:

(3)

Докажем, что для суженного линейного пространства кусочно-непрерывных функций введенное отображение (f,g) удовлетворяет аксиоме (4) скалярного умножения.

Пусть (f,f)==0 и точка -произвольная точка непрерывности функцииf, в которой f() 0. Тогда на [a,b], непрерывна ви .

По свойствам определенного интеграла , что противоречит предположениям.

Следовательно, в любой точке x непрерывности функции f выполняется равенство f(x)=0.

Пусть теперь -точка разрыва функцииf(x). Т.к. точек разрыва у функции конечное число, то для любой точки разрыва найдется ее проколотая окрестность, в которой функция f(x), будет непрерывна и, значит, равна нулю. Поэтому

, ,

т.к. f(x)=0 в точках непрерывности. Тогда, согласно условию (2), имеем равенство . Аналогично для точекa и b найдутся интервалы, в которых функция f(x) непрерывна. Следовательно, f(a+0)=0 и f(b-0)=0. В силу (3) получаем f(a)=f(b)=0.

Т.е.линейное пространство всех кусочно-непрерывных на отрезке [a,b] функций, удовлетворяющих условиям (2) и (3), является евклидовым пространством со скалярным произведением (1).

Определение: Неотрицательное число:

,

называется нормой функции f(x) в евклидовом пространстве. Учитывая, что

,

то норму функции можно записать в виде: .

Функция называется нормированной, если ее норма равна 1.

Определение: Две функции f(x) и g(x) называются ортогональными на [a,b], если их скалярное произведение равно нулю, т.е.

Пример: Функции f(x)=x и g(x)= являются ортогональными на отрезке [-1,1].

Вычислим скалярное произведение:

.

Пусть в евклидовом пространстве задана некоторая бесконечная последовательность элементов Эту последовательность называют ортонормированной системой, если для любых натуральныхi и j,

,

т.е. элементы этой последовательности попарно ортогональны и все имеют единичную норму.