§2 Ряды с неотрицательными членами

Будем рассматривать ряды вида

(1)

с неотрицательными членами (для любого натурального).

Теорема 1. Если последовательность частичных сумм ряда, с неотрицательными членами ограничена сверху, то ряд сходится.

Доказательство

Рассмотрим последовательность частичных сумм ряда с неотрицательными членами

Учитывая, что все члены ряда неотрицательны, приходим к выводу о том. Что последовательность неубывающая, т.е.

Так как последовательность ограничена сверху, то она имеет предел, что означает сходимость ряда (1).

Для решения вопроса о сходимости или расходимости ряда найдено много достаточных признаков. Рассмотрим некоторые из них.

Теорема 2. (первый признак сходимости)

Пусть имеются два ряда с неотрицательными членами

(а)

и

, (b)

Причем члены ряда (а) с некоторого номера, не превосходят членов ряда (b)

(2)

Тогда из сходимости ряда (b) следует сходимость ряда (а). Из расходимости ряда (a) следует расходимость ряда (b).

Рассмотрим, сначала, случай , т.е. случай выполнения неравенства (2) для любыхn. Тогда для частичных сумм рядов (а) и (b) будет выполняться неравенство.

(3)

Если ряд (b) сходится, то сходящаяся последовательность его частичных сумм ограничена, следовательно, последовательность частичных сумм ряда (а) ограничена сверху и по теореме 1 данного параграфа этот ряд будет сходиться.

Рассмотрим случай, когда ряд (а) расходится. Предположим, что и ряд (b) сходится. Тогда из неравенства (3) следует, что и ряд (а) должен сходиться. Получили противоречие, доказывающее второе утверждение теоремы.

В случае, когда вместо рядов (а) и (b) можно рассмотреть ряды, полученные из них путем отбрасывания первых членов, т.е. остатки этих рядов. По доказанному, утверждения теоремы будут справедливы для остатков рядов. Из материала предыдущего параграфа нам известно, что ряды и их остатки сходятся и расходятся одновременно, следовательно, теорема справедлива и в этом случае.

Примеры.

1. 

- сходится, как геометрическая прогрессия, исходный ряд тоже сходится.

2. ; ;

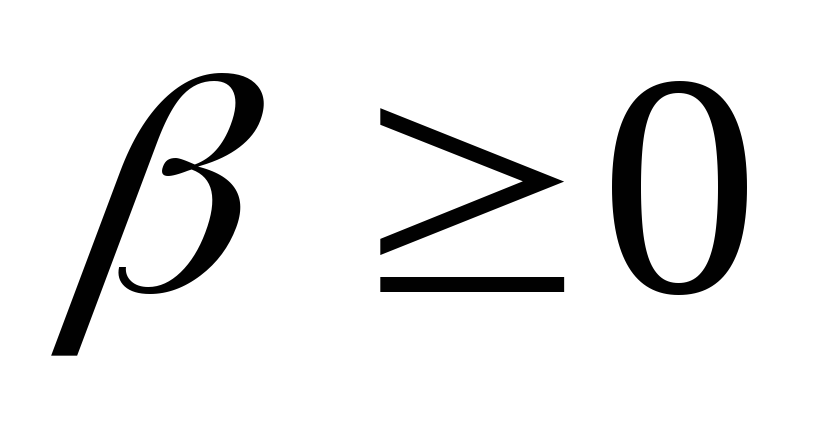
, . Но- расходится,;;- расходится.

3. Исследовать на сходимость ряд .

Из неравенства следует, что

Рассмотрим частичную сумму ряда .

.

Предел последовательности частичных сумм

.

По определению ряд сходится, а следовательно по первому признаку сравнения сходится исследуемый ряд.

Теорема 3. (второй признак сходимости)

Пусть имеются два ряда с неотрицательными членами

(а)

и

, (b)

кроме того, существует конечный, отличный от нуля, предел

Тогда ряды (а) и (b) сходятся или расходятся одновременно.

Доказательство.

По условию теоремы , т.к.то. Выберем произвольное, но такое, что. Это означает, что

Из определения предела следует, что найдется такой номер , что для всех

будет выполняться неравенство

. (4)

т.к. , то неравенство (4) можно записать в виде (5)

(5)

Если ряд сходится, то по свойствам сходящихся рядов сходится ряд , тогда из неравенства (5) следует, что, тогда по первому признаку сходимости рядсходится.

Если ряд расходится, то расходится и ряд. Из неравенства (5) следует, чтотогда согласно первому признаку сходимости будет расходиться ряд.

Проводя аналогичные рассуждения можно доказать, что из сходимости ряда следует сходимость ряда, а из расходимости рядаследует расходимость ряда.

Примеры.

Исследовать на сходимость ряд:

1. 

Удобно воспользоваться соотношением сравнения скоростей роста основных элементарных функций:

, ,; (4.3)

, ,; (4.4)

Но - сходится,-сходится

2. 

,

Сравним исследуемый ряд с гармоническим, тогда

, то - расходится.

Дополнение предельного признака сравнения

;

а) Если - ряды сходятся или расходятся одновременно;

б) Если - из сходимости рядасходимость ряда

в) Если - из расходимости рядарасходимость ряда

При применении признаков сравнения, можно использовать следующие соотношения.

Если -бесконечно малая функция, т.е., то приn стремящемся к бесконечности верны соотношения:

, ,,,

, ,,

, .

Эти соотношения следуют из замечательных пределов и следствий из них.

Также удобно использовать, что

, и

Теорема 4 (третий признак сравнения).

Пусть имеются два ряда с положительными членами

(а)

и

, (b)

Пусть начиная с некоторого номера m (т.е. для всех ) выполняется неравенство

(6)

тогда из сходимости ряда (b) следует сходимость ряда (а), из расходимости ряда (a) следует расходимость ряда (b).

Будем считать, что неравенство выполняется, начиная с . (В противном случае можно провести рассуждения относительно остатков рядов). Выпишем неравенства, следующие из условия теоремы

Перемножив неравенства (все члены рядов положительны), получим

.

Окончательно получаем

Из последнего неравенства и первого признака сравнения и следует утверждение теоремы.