§ 6 Пределы интегрирования, зависящие от параметра

Пусть функция определена в плоской области (S), ограниченной линиями y=c, y=d (c<d) и , где- функции, непрерывные на отрезке.

При каждом фиксированном существует. Каждому значениюбудет соответствовать определенное значение интеграла. Следовательно,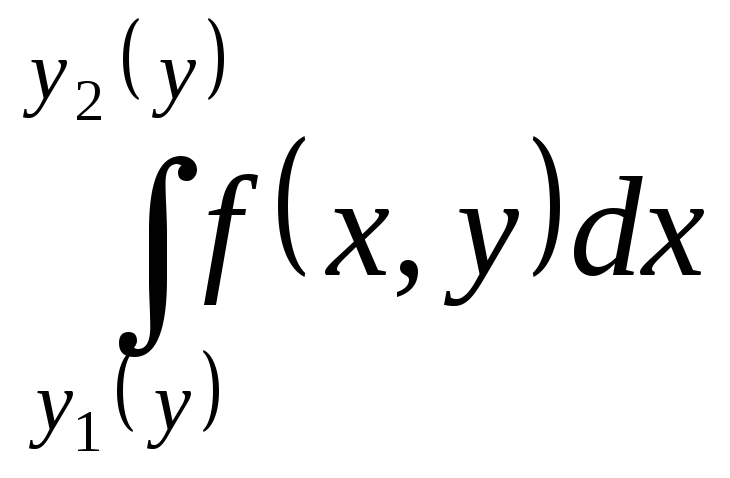является функцией переменной (параметра), определенной на отрезке. Введем обозначения:

(1)

Примем без доказательства два утверждения.

Теорема 1. Пусть функция непрерывна в плоской области (S) и . Тогда функциянепрерывна на отрезке.

Теорема 2. Пусть функция непрерывна в плоской области (S) и имеет на ней непрерывную частную производную . Пусть функцииопределены на отрезкеи имеют на нем непрерывные производные. Пусть. Тогда для любогосуществует, причем

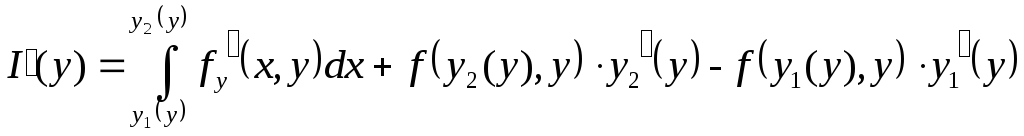
Пример Дан интеграл . Найти.

Подынтегральная функция непрерывна на всей плоскости Оху, следовательно, будет непрерывна в любом прямоугольнике, где. По теореме из §2 возможен предельный переход по параметру под знаком интеграла

.

Глава 18 несобственные интегралы, зависящие от параметра

§1 Определение равномерной сходимости

Пусть функция задана в областиПусть при каждом фиксированномнесобственный интегралсходится. Тогдабудет представлять собой функцию переменной (параметра)у, определенную на отрезке . Будем обозначать ее, где.

Наше утверждение, что несобственный интеграл сходится при каждом. Это означает, что при каждом фиксированном

.

Тогда

Используя свойства аддитивности определенного интеграла, запишем эквивалентную формулу

По определению это означает, что для каждого для любого > 0 найдется число М > 0 , такое, что из неравенства А>M будет следовать неравенство

Заметим, что число М выбирается по  > 0 для каждого , т.е. выбор его зависит и от и от у.

Если для  > 0 можно указать число М > 0, зависящее только от e (т.е. для всех одно и то же) такое, что из неравенства А>M будет следовать неравенство

Сразу для всех , то говорят, что несобственный интеграл сходится по параметруравномерно.

Аналогичным образом вводится понятие равномерно сходящегося по параметру несобственного интеграла второго рода.

Пусть функция задана в прямоугольнике(здесь- конечные числа).

Пусть при каждом фиксированном несобственный интеграл сходится. Тогдабудет представлять функцию переменной (параметра) .

Последнее утверждение означает, что при каждом фиксированном

.

(Мы ввели обозначения: ).

Последнее равенство по определению предела означает, что для каждого для любого e > 0 найдется такое число >0 , такое, что из неравенства

следует неравенство

Следует отметить, как и в случае несобственного интеграла первого рода, число >0, выбираемое по e будет, вообще говоря, для каждого свое.

Если же для любого e > 0 можно найти число >0 зависящее только от e (т.е. одно и то же для всех ), такое что из неравенства следует неравенство

,

То несобственный интеграл называется равномерно сходящимся по параметруу на отрезке .

§2 Непрерывность интеграла как функции параметра

Теорема. Пусть

1. функция непрерывна в прямоугольнике;

2. несобственный интеграл 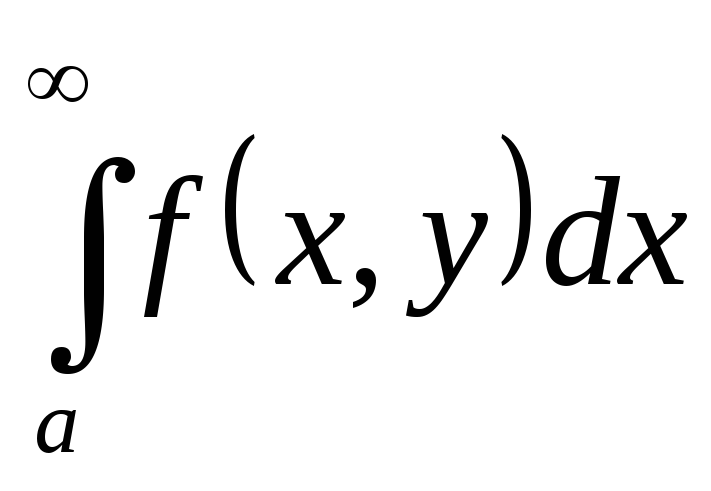сходится равномерно относительноу на отрезке .

Тогда функция непрерывна на отрезке .

Доказательство. Зафиксируем произвольное . Выберем произвольноеe > 0.

По условию теоремы интеграл сходится равномерно по переменнойу на отрезке ,поэтому по выбранному e > 0 найдем число М>0, зависящее только от e, такое, что для всякого числа А>M, сразу для всех будет выполняться неравенство

. (1)

Выберем и зафиксируем число А, удовлетворяющее условию А>M. Введем обозначение . В выбранных обозначениях неравенство (1), справедливое для всех , запишется в виде

(2)

Рассмотрим подробно разность, стоящую под знаком модуля в неравенстве (2)

- это собственный интеграл, зависящий от параметра. Из теоремы о непрерывности собственных интегралов, зависящих от параметра, следует, что непрерывна на отрезке ,а значит по теореме Кантора и равномерно непрерывна на нем.

Тогда для любого e > 0 найдется >0, зависящее только от e, такое, что для двух произвольных точек из ,для которых выполнено , тогда будет выполняться неравенство

.

Имеем

,

тогда

Если выбрать ,, где произвольное число, но такое, что , тогда будет выполняться неравенство. Это означает, что функциянепрерывна в точке. Так как мы выбирали произвольную точку ,то приходим к выводу о непрерывности функции на отрезке .

Теорема доказана.