§2. Равномерная сходимость функциональных последовательностей и рядов.
Функциональные ряды обычно начинают изучать с исследования его на сходимость, которое сводится к определению области сходимости этого ряда.
При этом можно использовать известные свойства числовых рядов и их признаки сходимости.
Таким образом, выделяют области абсолютной и условной сходимости.
Другая и более сложная задача теории функциональных рядов - нахождение их суммы.
Запишем определение поточечной сходимости последовательности на языке символов:
(1)
Определение.
Функциональная последовательность
называется равномерно сходящейся к
функции
на множестве Х, если
Замечание:
(3).
Замечание:
Отличие поточечной
и равномерной сходимости состоит в том,
что в первом случае номер
зависит от
и
,
а во втором - только от
.
Определение.
Ряд
,
членами которого являются функции,
определенные на Х, называетсяравномерно
сходящимся
на этом множестве, если последовательность
его частичных сумм равномерно сходится
на Х, то есть
и
(4)
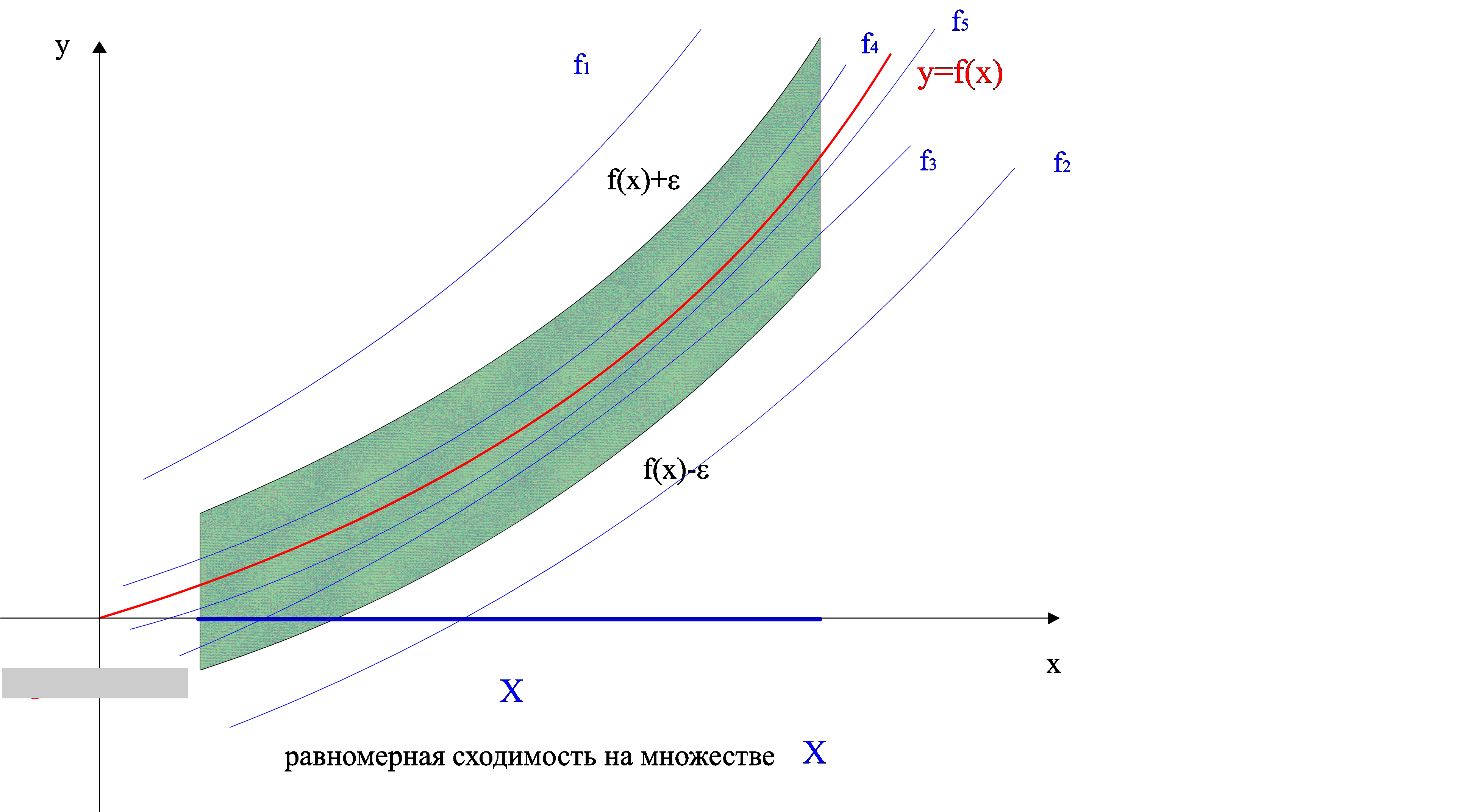
Для функционального ряда справедлива:
Теорема (признак Вейерштрасса).
Если члены
функционального ряда
удовлетворяют неравенствам:
(5) и числовой ряд
,
-сходится,
то функциональный ряд сходится равномерно
в области Х.
Доказательство:
Так как числовой
ряд сходится, то его остаток стремится
к нулю
,
то есть
и
по определению равномерной сходимости
ряд
-равномерно
сходится в области Х.
Числовой ряд
,
члены которого удовлетворяют неравенству
(2.5), называетсямажорантным
рядом или
мажорантой для функционального ряда
(1.1).
Функциональный ряд называется мажорируемым на множестве Х.
Замечание:
Признак Вейерштрасса является достаточным для абсолютной сходимости ряд.
Теорема
Для последовательности
функции 
и функции U(x),
определённых на множестве 
,
Справедливо следующее утверждение:
Справка:
Число называется верхней гранью множества Х, если:
уд. неравенству 
Для
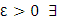
х
(или 
M’<M
x
: x>M’)
Доказательство:
а) Пусть {
по определению равн. сходимости:
n>n0(ε)
(*).
Поэтому для 
конечная точная верхняя грань:
Используя свойство точной верхней грани и определение (*) имеем:
б) Пусть 
Согласно свойству
точной верхней грани, для всех 
верно
неравенство:
т.е. 
Что по определению
означает, что 
.
последовательность
его частичных сумм равномерно сходится
на 
.
Следствие.
Для равномерной
сходимости функционального ряда
,
необходимо и достаточно, чтобы
Пример:
Выяснить, является ли функциональный ряд равномерно сходящимся:
По признаку Лейбница
этот ряд сходится в 
Оценим остаток
ряда 
:
В силу свойства точной верхней грани.
т.е. 
§3. Свойства равномерно сходящихся рядов
Замечание:
Если два функциональных ряда
и
сходятся на множествеX
равномерно,
то всякая их линейная комбинация ,
где,R
так же является равномерно сходящимся
рядом на множествеX.
Теорема
Если функции непрерывны в точке
ряд
- равномерно сходящийся на множествеX,
то его сумма
так же непрерывна в точке
.
Доказательство.
Напомним определение:
Функция непрерывна в точке
,
если она определена в этой точке,
существует предел функции в этой точке
и равен значению функции в точке, т.е.
или
Ряд
- равномерно сходящийся
Последнее неравенство
выполняется для 
,
в том числе и для любого фиксированного
,
т.е.
Частичная сумма ряда - функция
- непрерывна, как сумма конечного числа
непрерывных функций она непрерывна и
в точке
.
Оценим разность
т.е. 
,
т.е. функция 
- непрерывна в точке
Следствие 1.
Если сумма 
функционального ряда с непрерывными
членами разрывна
в области 
,
то этот ряд в области 
сходится неравномерно.
Следствие 2 В равномерно сходящемся ряде возможен почленный переход к пределу, т.е.
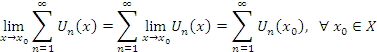
Т.к. 
- непрерывная функция, то 
Пример
Исследовать
характер сходимости ряда
на сегменте 0x1
при х=0 0+0+0+… ряд сходится;
при х=1 0+0+0+… ряд сходится;
Частичные суммы ряда
.
Тогда предел частичных сумм
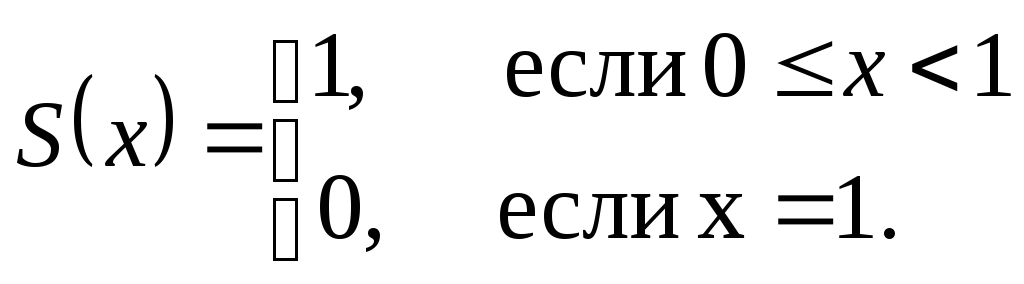
Остаток ряда
.
Следовательно, данный ряд сходится неравномерно на исследуемом отрезке.
Примечание. Если функциональный ряд непрерывных на сегменте функций сходится на этом сегменте к разрывной функции, то ряд сходится неравномерно.
Замечание (следствие теоремы о непрерывности суммы неравномерно сходящегося ряда)
Если сумма S(x) функционального ряда с непрерывными членами разрывна в области X, то этот ряд в области X сходится неравномерно.
Следствие
: В равномерно сходящемся ряде возможен
почленный переход к пределу.
– сходится равномерно
тогда
S(x)
- непрерывная функция.
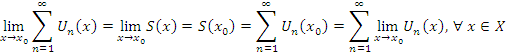
т.е.
Теорема (о почленном интегрировании функционального ряда).
Если функциональный
ряд
с
непрерывными членами сходится к функцииS(x)
равномерно на [a,b],
то его можно почленно интегрировать на
любом отрезке
и
справедливо равенство:
(1)
и ряд
сходится равномерно на отрезке [a;b].
Доказательство:
1.Согласно теореме
о непрерывности равномерно сходящегося
функционального ряда функция
непрерывна на отрезке [a;b],
следовательно, она интегрируема на
любом отрезке
.
2. Ряд
сходится равномерно на отрезке [a;b]
это означает, что
Обозначим:
Оценим разность:
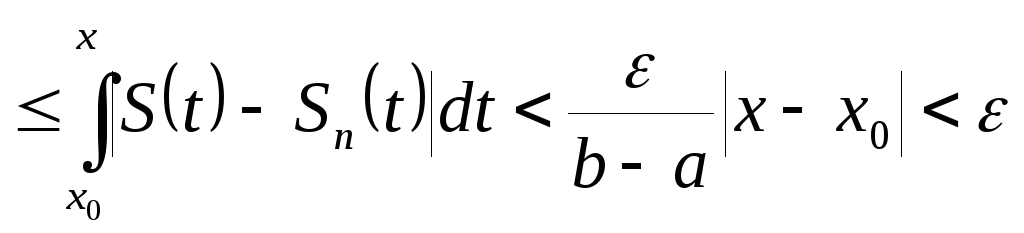
Для
,
следовательно, ряд
сходится на отрезке [a;b]
равномерно к функции
,
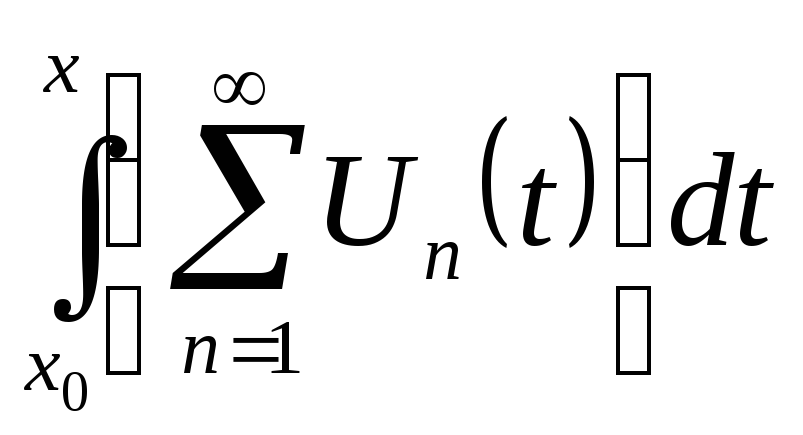т.е. справедливо равенство (1).
Пример:
Исследовать на
сходимость ряд
.
Рассмотрим ряд:
Для любого
действительного числа
,
а ряд
-
сходящийся, следовательно, по признаку
Вейерштрасса ряд
- сходится равномерно на всей числовой
оси.
Проинтегрируем его на отрезке [0;x]
По теореме о почленном интегрировании функциональных рядов он сходится равномерно на всей числовой оси.
Теорема ( о почленном дифференцировании функционального ряда)
Если функциональный
ряд с непрерывно дифференцируемыми на
отрезке [a;b]
членами сходится к функции S(x),
а ряд – сходится равномерно на этом
отрезке, то исходный ряд
-
сходится равномерно на[a;b]
, его сумма S(x)
– непрерывно дифференцируемая функция
и справедливо равенство
(2)
Доказательство:
Обозначим через
.
Проинтегрируем это равенство на
(Левая
часть полученного равенства дифференцируема
по x
, следовательно,
и правая
часть дифференцируема по x)
тогда
,
следовательно, справедливо равенство
(2).
Равномерная
сходимость ряда 
следует из предыдущей теоремы.
Пример:
Найти сумму ряда:
Ряд
сходится при .
.
сходится при
,
т.е. сходится равномерно по признаку
Вейерштрасса,
– сходится,
