§7 Умножение абсолютно сходящихся рядов

Определение.

Пусть имеются два ряда

(1)

и

. (2)

Ряд

, где(3)

называется произведением рядов (1) и (2).

Заметим, что произведение по аналогии с конечными произведениями можно располагать различными способами. На рисунке 7.1 произведение и группировка слагаемых осуществляется «по диагонали». На рисунке 7.2 «по квадратам».

Первый способ приводит к сумме

(4)

Второй способ приводит к сумме

(5)

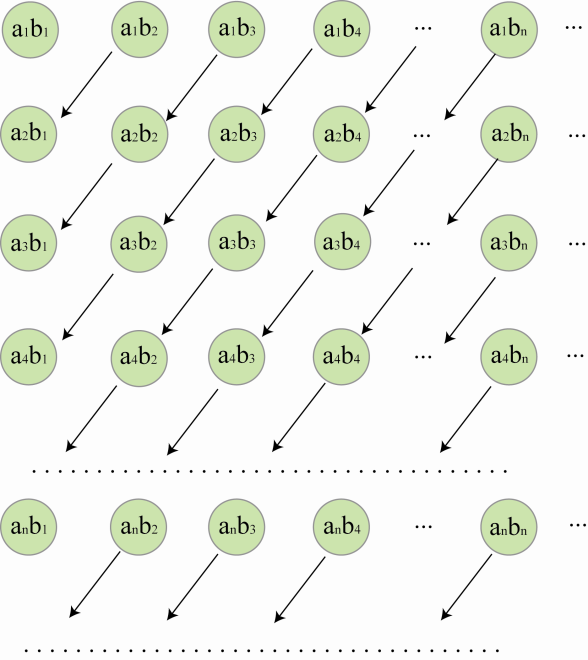
Рис. 7.1

Рис. 7.2

Теорема (Коши) Если ряды (1) и (2) сходятся абсолютно и имеют суммы А и В, то произведение этих рядов сходится абсолютно и имеет сумму АВ.

Доказательство. Рассмотрим ряды, составленные из абсолютных величин членов рядов (1) и (2)

(6)

и

(7)

Следуя [2], обозначим суммы рядов (6) и (7) (по условию теоремы ряды (6) и (7) сходятся).

Расположим члены ряда-произведения произвольным образом

(8)

Рассмотрим ряд

(9)

и его частичную сумму, при этом введем обозначение

Следовательно, ряд (3) сходится абсолютно.

Для нахождения суммы этого ряда расположим его члены, как на рис. 7.2 («по квадратам»).

Обозначаем привычным образом частичные суммы рядов (1) и (2) исоответственно. Тогда последовательность частичных сумм ряда (5) можно записать в виде

Эта последовательность сходится к , следовательно, это и есть сумма ряда (3).

Теорема доказана.

Замечание 1. Если ряды (1) и (2) сходятся не абсолютно, то ряд (3) может сходиться, а может и расходиться.

Замечание 2. Имеет место теорема Мартенса. Если ряды (1) и (2) сходятся, причем один из них абсолютно, то их произведение (3) сходится и справедливо соотношение

, (10)

Где А, В, С – суммы рядов (1), (2), (3) соответственно.

Замечание 3. (Теорема Абеля)

Если каждый из рядов (1) и (2) сходится условно, а также ряд (3) сходится, то для сумм этих рядов справедливо равенство (10).

Глава 15. Функциональные ряды.

§1. Функциональные ряды. Основные понятия.

Пусть -последовательность функций, заданных на некотором множестве Х.

Определение. Выражение вида (1)

в котором члены последовательности соединены знаками плюс, называютфункциональным рядом, определенным на множестве Х.

Функции - члены этого функционального ряда.

При фиксированном всякому функциональному рядусоответствует числовой ряд, членами которого являются значенияфункцийв точке.

Определение. Функциональный ряд (1.1) называют сходящимся в точке , если сходится числовой ряд.

Точка называется точкой сходимости функционального ряда (1.1) . Множество всех точек сходимости функционального ряда называется его областью сходимости.

Такую сходимость функционального ряда называют поточечной.

Определение. Конечная сумма называетсяn-ной частичной суммой ряда(1.1).

Определение. Функция , определенная в областиD называется суммой ряда (1.1).

Определение. Для всякого функциональный ряд,называютn-ным остатком функционального ряда (1.1).

Можно записать критерий Коши сходимости функционального ряда.

Функциональный ряд (1.1) сходится на множестве Х тогда и только тогда, когда для и(зависящее от х и), такое, что для всехи

Определение. Функциональный ряд (1.1) называется абсолютно сходящимся на множестве , если в любой точкеk этого множества сходится ряд

Замечание. Для определения абсолютной сходимости функционального ряда используют признаки Коши и Даламбера.

Примеры.

Найти область сходимости:

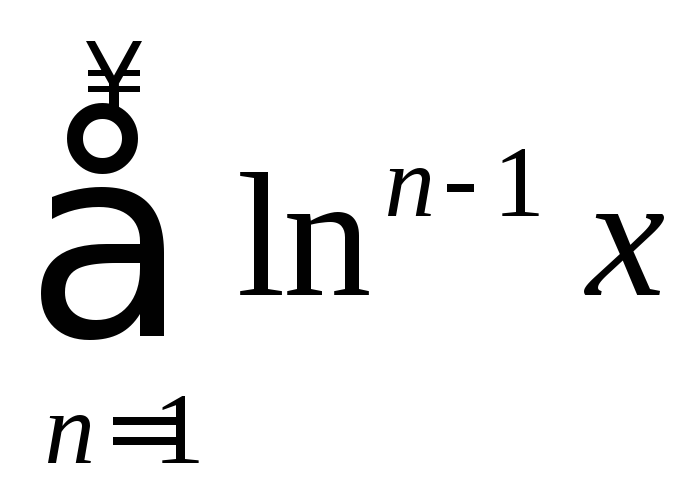1. , Область определения: _.

-это геометрическая прогрессия,у которой

, ряд сходится при,

; ; т.е. при- ряд сходится.

Легко найти и сумму этого ряда: .

2. Область определения:.

- сходится по признаку сравнения исходный ряд сходится абсолютно _{область сходимости исследуемого ряда}.

3. Область определения :,

; значит ряд сходится при

Решим неравенство:

;

- ряд абсолютно сходится;

-расходится;

при :

Ряд условно сходится по признаку Лейбница .