§3 Интегральный признак Коши

Теорема (интегральный признак Коши).

Пусть имеется ряд с положительными монотонно убывающими членами

(1)

и пусть непрерывная, положительная, монотонно убывающая функция, такая что

(2)

Тогда

1) Если несобственный интеграл сходится, то сходится и ряд (1);

2) Если указанный интеграл расходится, то расходится и ряд (1).

Для доказательства рассмотрим геометрическую интерпретацию интеграла и частичных сумм ряда (1).

Рис. 1

Рис. 2

Рисунок 1 поясняет тот факт, что площадь ступенчатой фигуры равна (т.к. площадь одного прямоугольника равна произведению соответствующего члена ряда- высоты на единицу – длину основания)

.

С другой стороны, площадь криволинейной трапеции, ограниченной графиком функции, прямыми и осью ОХ можно вычислить с помощью определенного интеграла. Имеем неравенство

(3)

На втором рисунке площадь ступенчатой фигуры

.

В результате приходим к неравенству

,

Тогда

(4)

Теперь рассматриваем случай, когда несобственный интеграл сходится, тогда существует конечная величина

Так как

,

с учетом неравенства (4), получаем

.

Следовательно, возрастающая последовательность частичных сумм ряда (1) ограничена сверху, значит, она имеет предел, а ряд, по определению, сходится.

Если интеграл расходится, т.е.

из неравенства (3) будет следовать, что последовательность частичных сумм неограниченно возрастает, следовательно, ряд (1) расходится.

Пример.

Исследовать на сходимость обобщенный гармонический ряд

Применим интегральный признак сходимости ряда. Рассмотрим несобственный интеграл

.

а) если

b) Если

В этом случае интеграл и обобщенный гармонический ряд сходятся.

с) Наконец,

Интеграл и ряд расходятся.

§4 Признаки сходимости рядов с положительными членами

Теорема 1 (признак Даламбера).

Дан ряд с положительными членами

(1)

Если существует конечный предел

. (2)

Тогда:

1. при ряд (1) сходится;

2. при ряд (1) расходится.

Доказательство. Воспользуемся определением предела последовательности. Рассмотрим случай, когда , выберем произвольное числотак, чтобы число.

Из определения предела последовательности следует, что начиная с некоторого номера , для всехвыполняется неравенство

(3)

Воспользуемся неравенством . тогда

…………………………..

Ряд присходится, то сходится ряд, являющийся остатком ряда (1), а следовательно, сходится ряд (1).

2). Рассмотрим случай, когда ,

Тогда из неравенства (3) следует, что

Следовательно, начиная с номера не выполняется необходимое условие сходимости ряда, значит в этом случае ряд (1) расходится.

Пример. Исследовать сходимость ряда .

Воспользуемся признаком Даламбера. Найдем

.

Далее находим предел

.

Из полученного результата делаем вывод, что исследуемый ряд сходится.

Терема 2 (признак Коши). Пусть для ряда (1) с положительными членами существует предел

(4)

Тогда

1. если , то ряд (1) сходится;

2. Если , то ряд расходится.

Воспользуемся определением предела последовательности.

Рассмотрим случай, когда . Выберем произвольное, достаточно малое число, так чтобы(рис. 3)

Рис. 3

Тогда из равенства (4) следует, что существует такой номер , что для всех

Будет выполняться неравенство

(5)

Из неравенства (5) следует, что для

.

Из сходимости ряда и признака сравнения ряд (1) в этом случае сходится.

2) Пусть .

Тогда, обозначив , из определения предела получаем, что для

. Тогда из расходимости ряда() и признака сравнения следует расходимость ряда (1).

Примеры.

1. Исследовать на сходимость ряд .

Применим признак Коши. Найдем

.

Исследуемый ряд сходится.

2. Исследовать на сходимость ряд

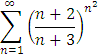
Следовательно, исследуемый ряд сходится.

Замечание 1

Если в признаке Коши или в признаке Даламберато эти признаки не дают ответа на вопрос о сходимости исследуемого ряда.

Замечание 2

При использовании радикального признака Коши удобно использовать формулу Стирлинга и следствие из неё ([Ф] т2. стр. 369-371.))

, тогда

3. Пример: Исследовать на сходимость ряд, при

Следовательно, при , ряд сходится, а при - расходится

Приведем без доказательства несколько признаков сходимости рядов с положительными членами ([2] стр. 266-271, [Ф] т2. стр. 305-320.)

Признак Раабе

Пусть дан ряд (1) с положительными членами. Пусть

и существует конечный или бесконечный предел . Тогда:

1) если то ряд (1) сходится;

2) если то ряд (1) расходится.

Признак Бертрана

Пусть дан ряд (1) с положительными членами. Пусть

и существует конечный или бесконечный предел . Тогда:

1) если то ряд (1) сходится;

2) если то ряд (1) расходится.

Замечание

Если в признаке Раабе или в признаке Бертранато эти признаки не дают ответа на вопрос о сходимости исследуемого ряда.

Признак Гаусса.

Пусть дан ряд (1) с положительными членами. Пусть отношение можно представить в виде

,

где - постоянные,- ограниченная величина (т.е.). Тогда

1. (- любое), то ряд (1) сходится;

2. (- любое), то ряд (1) расходится;

3. , , то ряд (1) сходится;

4. , , то ряд (1) расходится.