
- •Глава 14 Числовые ряды с действительными членами
- •§1 Основные понятия и простейшие свойства рядов
- •§2 Ряды с неотрицательными членами
- •§3 Интегральный признак Коши
- •§4 Признаки сходимости рядов с положительными членами
- •§5 Знакочередующиеся ряды
- •§ 6 Знакопеременные ряды
- •§7 Умножение абсолютно сходящихся рядов
- •Глава 15. Функциональные ряды.
- •§1. Функциональные ряды. Основные понятия.
- •§2. Равномерная сходимость функциональных последовательностей и рядов.
- •§3. Свойства равномерно сходящихся рядов
- •§4 Степенные ряды
- •§5. Свойства степенных рядов.
- •§6. Ряды Тейлора
- •§7 Разложение элементарных функций в ряд Маклорена
- •§8 Методы разложения функций в ряд Тейлора
- •Приближенное вычисление интегралов
- •Интегрирование дифференциальных уравнений
- •Глава 16 Ряды Фурье
- •§1.Ортонормированные системы.
- •§2.Основная тригонометрическая система функций
- •§3.Ряды Фурье по ортогональным системам функций
- •Тригонометрические ряды Фурье
- •§4.Экстремальное свойство коэффициентов Фурье. Неравенство Бесселя и его следствия.
- •Тригонометрические ряды Фурье для четной, нечетной функций
- •§5 Комплексная форма тригонометрического ряда Фурье
- •§6 Интеграл Фурье. Преобразование Фурье
- •Глава 17
- •§1 Определение интегралов, зависящих от параметра
- •§2 Предельный переход под знаком интеграла
- •§ 3 Непрерывность интеграла как функции параметра
- •§ 4 Дифференцирование интегралов по параметру
- •§ 5 Интегрирование интегралов по параметру
- •§ 6 Пределы интегрирования, зависящие от параметра
- •Глава 18 несобственные интегралы, зависящие от параметра
- •§1 Определение равномерной сходимости
- •§2 Непрерывность интеграла как функции параметра
- •§3 Интегрирование по параметру под знаком интеграла
- •§ 4 Дифференцирование по параметру под знаком интеграла
- •§5 Признак равномерной сходимости несобственных интегралов
§3 Интегрирование по параметру под знаком интеграла
Теорема. Пусть
функция
![]() непрерывна в области
непрерывна в области
 сходится равномерно
относительно у
на
сходится равномерно
относительно у
на
 .
.
Тогда справедливо равенство:
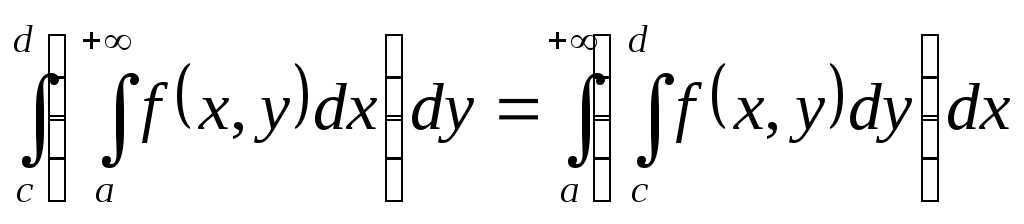 ,
(1)
,
(1)
причем несобственный интеграл, стоящий в правой части равенства (1) сходится.
Доказательство.
Возьмем произвольное e
> 0. По условию теоремы
![]() сходится равномерно относительноу
на
сходится равномерно относительноу
на
![]() ,
поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех
,
поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех
![]() будет выполняться неравенство
будет выполняться неравенство
![]() .
.
Зафиксируем
некоторое число А, удовлетворяющее
неравенству А>M.
Вводя как и раньше обозначения
![]() ,
сразу для всех
,
сразу для всех
![]() неравенство можно записать в виде
неравенство можно записать в виде
![]()
Так как функции
![]() и
и![]() непрерывны на отрезке
непрерывны на отрезке
![]() ,
то они и интегрируемы на нем. В силу
свойств интегралов
,
то они и интегрируемы на нем. В силу
свойств интегралов
![]()
тогда
![]()
Мы получили, для любого e > 0 существует число М, что при любом А>M, выполняется неравенство
![]() .
.
Это означает что
![]() ,
(2)
,
(2)
но
![]() - собственный интеграл, зависящий от
параметрау.
По теореме
об интегрировании по параметру
собственного интеграла можем записать
- собственный интеграл, зависящий от
параметрау.
По теореме
об интегрировании по параметру
собственного интеграла можем записать
 .
.
Тогда равенство (2) можно записать в виде

Ранее мы доказали существование предела, следовательно можно его записать иначе

Следовательно доказана сходимость интеграла, из правой части равенства (1) и справедливость самого равенства.
Теорема доказана.
§ 4 Дифференцирование по параметру под знаком интеграла
Теорема.
Пусть функция
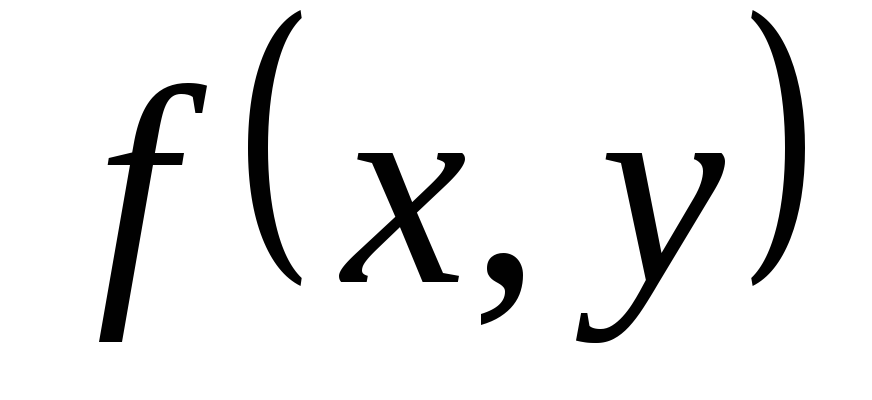 непрерывна в области
непрерывна в области и имеет в ней непрерывную частную
производную
и имеет в ней непрерывную частную
производную ;
; сходится при
каждом
сходится при
каждом
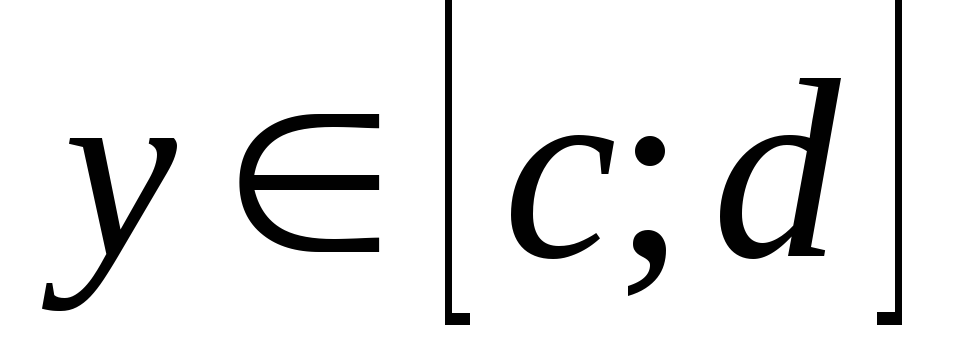 ;
;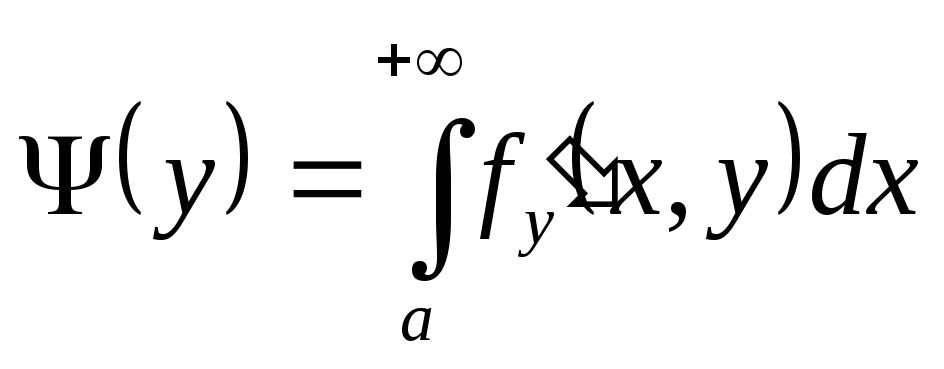 сходится равномерно
относительно у
на
сходится равномерно
относительно у
на
 ;
;
Тогда:
 существует при
каждом
существует при
каждом
 ;
; ,
т.е.
,
т.е.
 ;
; непрерывна на
непрерывна на
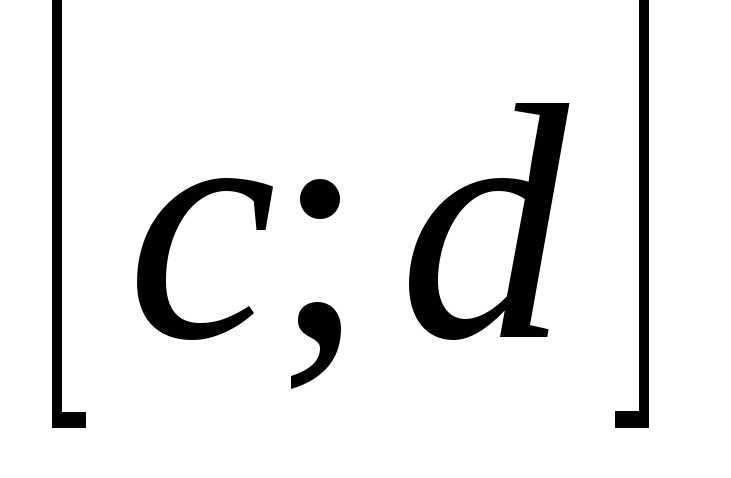 .
.
Доказательство:
Так как
![]() непрерывна в области
непрерывна в области и
и![]() сходится равномерно относительноу
на
сходится равномерно относительноу
на
![]() то по теореме из §2 и
то по теореме из §2 и
![]() существует. В частности существует
интеграл
существует. В частности существует
интеграл![]() для любого
для любого![]() ,
удовлетворяющего условию
,
удовлетворяющего условию![]() По теореме из §3 имеем
По теореме из §3 имеем
 .
.
Но
![]() .
Поэтому
.
Поэтому
 ,
,
следовательно
![]()
В правой части последнего равенства стоит интеграл с переменным верхним пределом от непрерывной функции, тогда по теореме Барроу
![]() .
.
Последнее равенство
справедливо для любого
![]() .
Таким образом доказано
.
Таким образом доказано
 существует при
каждом
существует при
каждом
 ;
;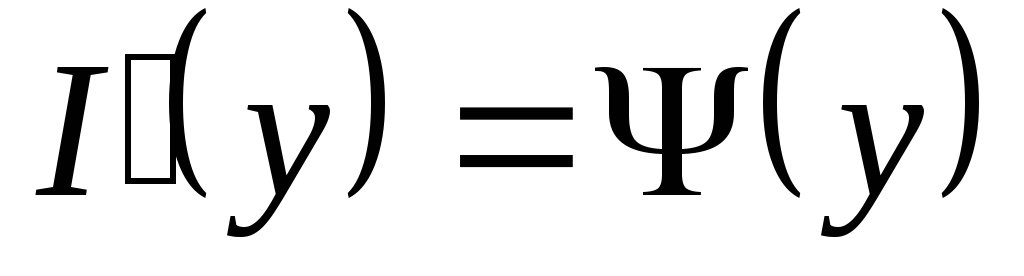 ,
,
 ;
;
3.![]() непрерывна на
непрерывна на
![]() т.к.
т.к.
![]() непрерывна на
непрерывна на
![]() .
.
§5 Признак равномерной сходимости несобственных интегралов
Теорема.
Пусть функция
 непрерывна в области
непрерывна в области
Функция
 определена и непрерывна на
определена и непрерывна на ;
; при всех значениях
при всех значениях
 и
и
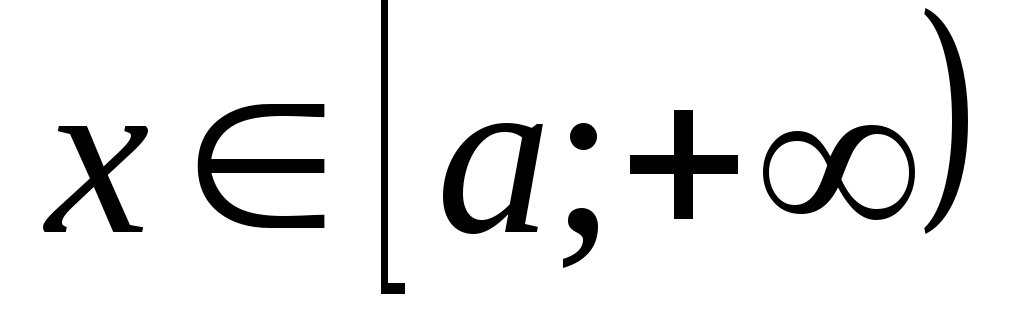 .
.
Тогда, если
несобственный интеграл
![]() сходится, то несобственный интеграл
сходится, то несобственный интеграл![]() сходится равномерно относительноу
на
сходится равномерно относительноу
на
![]() .
.
Утверждение примем без доказательства.
Замечание. Для несобственных интегралов второго рода, зависящих от параметра имеют место теоремы, аналогичные вышеизложенным.
