§ 3 Непрерывность интеграла как функции параметра

Теорема. Пусть функция непрерывна в прямоугольникеи. Тогда функциянепрерывна на отрезке.

Зафиксируем произвольное . В предыдущем параграфе было доказано, что

, в других обозначениях это означает

Следовательно, функция непрерывна в точке.

Замечание 1. Условие непрерывности функции в прямоугольникеявляется достаточным для непрерывностина отрезке.

Замечание 2. Аналогично можно доказать утверждение: Если функция непрерывна в прямоугольникеиТогда функциянепрерывна на отрезке.

Следствие. Если функция непрерывна в прямоугольнике, то одновременно непрерывны функциина отрезкеинепрерывна на отрезке. Тогда одновременно существуют интегралы

,

Эти интегралы называются повторными.

§ 4 Дифференцирование интегралов по параметру

Теорема. Пусть функция непрерывна в прямоугольникеи имеет в нем непрерывную частную производную. Пусть.

Тогда:

1. функция имеет на отрезкепроизводную;

2. т.е. ;

3. непрерывна на отрезке .

Доказательство. Зафиксируем произвольную точку . Дадим приращениетаким образом, чтобы. Вычислим значение функциии:

Найдем отношение приращения функции к приращению аргумента:

(1)

Согласно теореме Лагранжа

,

где . Тогда

. (2)

По условию теоремы частная производная непрерывна. Перейдем в соотношении (2) к пределу при. Учитывая теорему о предельном переходе под знаком интеграла, получаем

Следовательно, существует и. В силу произвольности, делаем вывод о том, чтосуществует на всем отрезке, кроме того,

. (3)

По условию теоремы непрерывна, тогда из соотношения (3) и теоремы о непрерывности интеграла как функции параметра следует непрерывностьна отрезке.

§ 5 Интегрирование интегралов по параметру

Теорема. Пусть функция непрерывна в прямоугольникеи. Тогда

(1)

Доказательство: Докажем более общее равенство:

(2)

Рассмотрим левую часть равенства (2). В силу непрерывности функции функциятакже непрерывна на отрезке. Таким образом, в левой части равенства (2) мы имеем интеграл от непрерывной функции с переменным верхним пределом. Применим к нему теорему Барроу

. (3)

Рассмотрим теперь правую часть равенства (2). Введем обозначение

(4)

Данная функция определена в прямоугольнике . Докажем что она и непрерывна в этом прямоугольнике. Выберем произвольную точкудадим приращение обеим переменным, так чтобы точка. Получаем

(5)

Пусть . Если, тоиодновременно. Возьмем произвольноеи воспользуемся непрерывностью функциив прямоугольнике, тогда для выбранногонайдется, такое что, как толькобудет выполняться неравенство:

.

Тогда если будет выполняться неравенство:

.

Это означает, что

Функция непрерывна в прямоугольнике(замкнутом множестве), то она на нем ограничена, следовательно, существует такое положительное число М, что

в прямоугольнике . Тогда

.

Это означает, что 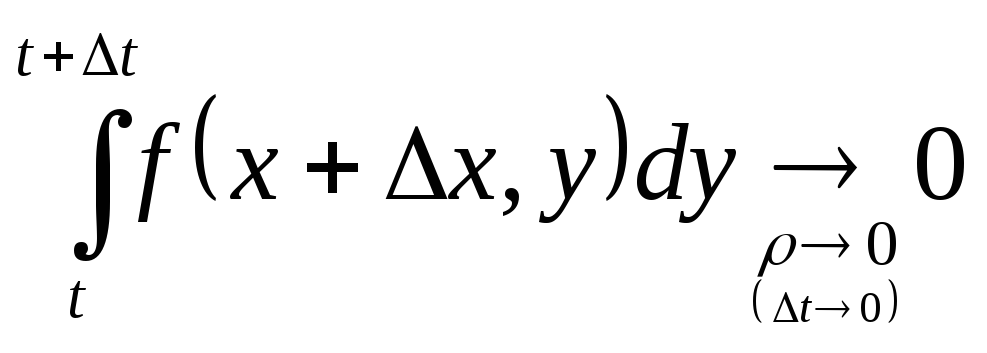. Тогда из соотношения (5), получаем, что

,

что означает непрерывность функции в произвольной точке, следовательно, функциянепрерывна в прямоугольнике. Из соотношения (4) по теореме Барроу следует

. (6)

По условию теоремы функция непрерывна в прямоугольнике, следовательно, инепрерывна в этом прямоугольнике. С учетом равенства (4), запишем правую часть равенства (2) в виде

. (7)

В правой части равенства (7) переменная выступает в качестве параметра. Ранее мы показали, что функциянепрерывна в прямоугольникеи имеет в нем непрерывную частную производную. По теореме о дифференцировании по параметру под знаком интеграла получаем

. (8)

Из анализа соотношений (3) и (8) приходим к выводу о том, что левая и правая части равенства (2) имеют на отрезке совпадающие производные, следовательно, они отличаются на константу.

. (9)

В последнем равенстве положим , получим, тогдаи получаем равенство

. (10)

Наконец, положив , получаем требуемое равенство

Теорема доказана.