Тригонометрические ряды Фурье для четной, нечетной функций

Напомним, что если функция f(x) определена на отрезке и является четной, т.е. для всехвыполняется равенствоf(-x)=f(x) и , а если является нечетной, т.е для всехвыполняется равенствоf(-x)=-f(x), то.

Произведение четной функции на четную или нечетной на нечетную является четной функцией. А произведение четной на нечетную является нечетной функцией.

Пусть f(x)- четная кусочно-непрерывная функция задана на отрезке.

Тогда тригонометрический ряд Фурье принимает вид:

,

соответствующие коэффициенты:

Если функция f(x) на этом отрезке нечетная, тогда:

,

Замечание: основная тригонометрическая система функций является ортогональной на любом отрезке длиной . Если функцияf(x) определена на всей числовой прямой и является периодической с периодом ,то соотношения (4),(5) позволяют вычислить коэффициенты Фурье ее ряда Фурье по основной тригонометрической системе на отрезке:

Так как интеграл от периодической функции с периодомT по отрезку длиной T не изменяется, когда отрезок интегрирования сдвигается вдоль числовой оси.

Замечание: Рассмотрим функцию f(x), заданную на отрезке и удовлетворяющую на нем условиям теоремы Дирихле. Разложим эту функцию на этом отрезке в тригонометрический ряд Фурье. В такой постановке задача не имеет однозначного решения, так как она многовариантна.

1.Эту функцию можно разложить в тригонометрический ряд Фурье на отрезке , как на произвольном отрезке. В этом случае суммаS(x)полученного ряда будет -периодической функцией.

2. Можно доопределить данную функцию в полуинтервале произвольным образом, лишь бы полученная функция на отрезкепродолжала удовлетворять условиям теоремы Дирихле. Разложим эту функцию в тригонометрический ряд Фурье на отрезкеи, рассмотрев сумму данного ряда только на отрезке, получим еще одно представление исходной функцииf(x) на отрезке в виде тригонометрического ряда Фурье. В этом случае суммаS(x) полученного ряда будет -периодической функцией.

Если доопределим исходную функцию четным образом, то получим тригонометрический ряд Фурье, не содержащий членов с синусами. Такое разложение называют разложением в тригонометрический ряд Фурье по косинусам.

Если доопределим исходную функцию нечетным образом, то получим разложение в тригонометрический ряд Фурье по синусам.

3.Если первоначально функция задана на отрезке , ее можно доопределить на произвольном отрезке, содержащем отрезок, так чтобы полученная функция продолжала удовлетворять на отрезкеусловиям теоремы Дирихле. Затем разложить доопределенную функцию в тригонометрический ряд Фурье на отрезкеи рассматривать его сумму только на отрезке. Сумма этого ряда Фурье функцииf(x) на отрезке будет-периодической функцией, причем.

Пример

Разложить функцию в ряд Фурье в интервале (-p;p).

Функция удовлетворяет условиям теоремы Дирихле и является чётной, следовательно

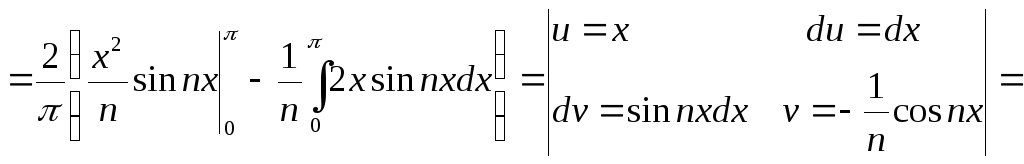
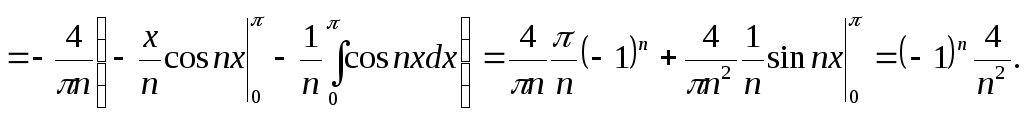
Следовательно

Положив в этом равенстве x=0, найдём

Если же записать равенство Парсеваля для данного разложения функции , то получим формулу

Следовательно